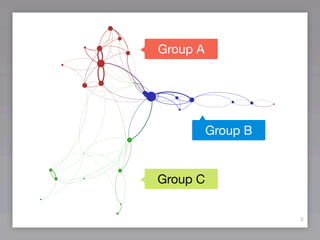
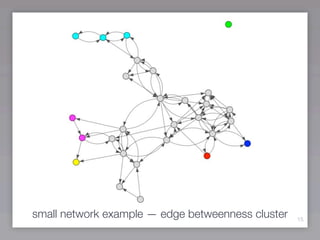
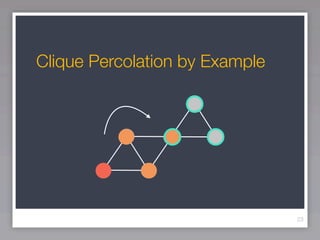
This document discusses community detection methods for identifying groups within networks. It begins with an overview of community detection and its relevance. It then discusses the basic idea behind community detection algorithms, which aim to identify communities as groups of nodes that are more densely connected internally than externally. The document outlines some notable algorithms like edge betweenness and clique percolation. It also covers limitations regarding technical aspects like runtime and memory needs, and methodological issues around evaluation and comparison of algorithm results.

1. Identifying Communities on
Twitter: Time, Topics & Clusters
Pascal Jürgens (@pascal)
Dept. of Communication, U of Mainz, Germany
1

2. Overview
Overview
Relevance
/ Why it’s interesting
The Basic Idea
/ Why it works
Limitations
/ When it works
Algorithms / How it works
Evaluations / How to tell whether it works
2

3. What Science are we in,
anyways?
“
The antireductionist catch-phrase, “the whole is more than the
sum of its parts,” takes on increasing significance as new
sciences such as chaos, systems biology, evolutionary
economics, and network theory move beyond reductionism to
explain how complex behavior can arise from large collections
of simpler components.
”
Mitchell, 2009 — Complexity: A Guided Tour
3

4. What Science are we in,
anyways?
Interdisciplinary territory with distinct influences
20th century Sociology — small-scale social network analysis
Econometrics — time-series analysis, predictions & forecasting
Mass Communication — media effects
Theoretical Physics — abstract, high-level descriptions of
networks; large-scale network analysis (Why is this even here?)
4

5. What is Community Detection?
“
Communities are groups of vertices which probably share common
properties and/or play similar roles within the graph.
”
Fortunato & Castellano 2009 — Community Structure in Graphs in the
Encyclopedia of Complexity and Systems Science
An exploratory method for partitioning a network into smaller pieces.
In many ways it is comparable to cluster analysis.
5

6. (Caveat Emptor)
CD is a complex, fairly new set of statistical methods for
exploratively building groups from data
So why not use simpler, better-known methods such as
clustering?
By all means, use simple methods!
(but they do something different)
6

7. Relevance
Networks are a fundamental structure of the world
There are global properties of networks (diameter &c.)
There are properties of nodes (centrality &c.)
However — Networks are almost never homogenous!
There is a structure hidden within the whole
7

8. Group A
Group B
Group C
8

9. Applications
Identify separate groups within relevant population for further
description
Captures “public sphere” better than aggregates such as
#hashtags
(Users who share a #tag might have nothing in common)
Investigate relationship of communities (mesoscopic graph)
In general: more accurate, delivers more details
9

10. Terminology
Graph: A network, consisting of
nodes (or vertices) such as twitter users
- with degree = number of connections
links (or edges) such as relationships via @-messages
with weight = intensity of links
Partition: one way to split a network into a set of communities
(k-) Clique: a set of k completely connected nodes
10

11. The Basic Idea
Communities: Local structures within a network that differ in their
structure from the surroundings
A good starting point: communities are better connected among
themselves than with other communities
Opens up two obvious methods:
Add links between close nodes until some condition is met
Remove links between distant nodes until some condition is met
11

12. possible Partitions 12

13. The Edge Betweenness
Algorithm (Girvan / Newman)
Edge betweenness: the number of shortest paths between any
two nodes that go through one edge
High EB: the link is very important to fast information flow
Low EB: the link can easily be replaced by using another way
The algorithm simply eliminates the links with the highest EB step
by step
An optimal cut can be selected from the sequence of partitions
13

14. small network example 14

15. small network example — edge betweenness cluster 15

16. Limitations — Technical
The number of potential ways to divide a network grows super-
exponentially with the number of nodes (!)
Two critical performance parameters of algorithms: runtime (“Big-
O”-notation) and memory
Networks up to 100s of nodes and/or edges — usually OK
Networks up to 10 000s of nodes and/or edges — buy a lot of
memory (8GB upwards) and prepare to wait
Bigger networks: Ask a computer scientist
16

17. Limitations — Methodological
Quality of partitions — algorithms don’t guarantee best results
Instability of partitions — algorithms can be non-deterministic and
very sensitive to small changes
Evaluation / Comparison of partitions is near-impossible
Sometimes result is not one best but a whole set of partitions
Nodes can only belong to one community (!)
17

18. large network example — edge betweenness cluster 18

19. Notable Algorithms
The Edge Betweenness Algorithm (Girvan / Newman)
Markov Cluster Algorithm (MCL, van Dongen, this one is in
gephi)
Clique Percolation (CPM, Palla et al.)
Information theoretical Algorithm (Roswall & Bergstrom, does
hierarchies and works with communities of very different sizes)
19

20. A Word about MCL
Marked as experimental in gephi and hard to use (clustering panel
needs to be open before loading dataset), but the only clustering
algorithm available
Based on probability of link use - simulates flow through the
network
Often sub-stellar results
Connection probabilities seem an odd predictor for empirical
connection habits
DEMO
20

21. Clique Percolation
One among several new algorithms that address shortcomings
Intuitive mechanism
Nodes can be in several communities!
Works rather well for dense networks!
21

22. Clique Percolation
Idea: Find k-cliques in the network
Try to “move” the cliques until they reach a bottleneck that they
can’t fit through
All the nodes covered by this “trail” are assigned to a community
Rather easy to implement in software (igraph) plus free
implementation available (CFinder, cfinder.org)
DEMO
22

23. Clique Percolation by Example
23

24. Evaluation
Exploratory methods are notoriously difficult to assess (beyond
rule-of-thumb judgements).
Two ways allow rigorous examination:
Comparison of two partitions
Comparison of a partition agains a baseline model (zero model)
Effectively unfeasible for non-mathematicians: Pick a good
algorithm and treat results with care
24

25. What about user attributes?
What happens when we use empirical attributes to group users?
Example of the German General Election 2009: Measured party
affiliation (wahlgetwitter hashtag +/- convention)
Turns out, users don’t cluster by party affiliation
But careful: this approach means measuring with two loose ends
Clustering baseline needs to be really, really solid
25

26. Takeaway
Community detection used to be hard but is pretty usable now
Think about the design and scope of a collected network
beforehand! (timeframe, directed, size/scope etc.)
Watch the outliers (Justin Bieber will sink your analysis)
Choose an algorithm that
uses directed & weighted links, is understandable, robust
and one that produces meaningful, simple results!
26

27. Thanks!
27

28. Literature
Fortunato, Santo and Castellano, Claudio (2009): Community
Structure in Graphs. In: Meyers, Robert A. (Ed.): Encyclopedia of
Complexity and Systems Science. Springer.
Lancichinetti, Andrea and Fortunato, Santo: Community detection
algorithms: a comparative analysis. Phys. Review E.
Mitchell, Melanie (2009): Complexity: A Guided Tour
Palla, Gergely; Barabási, Albert-László and Vicsek, Tamás ():
Quantifying social group evolution
28