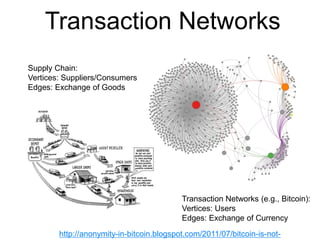
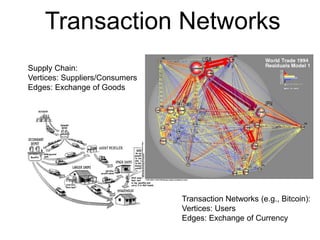
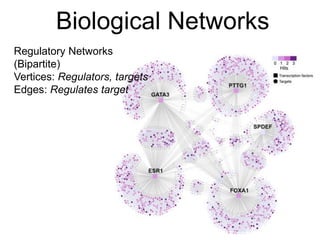
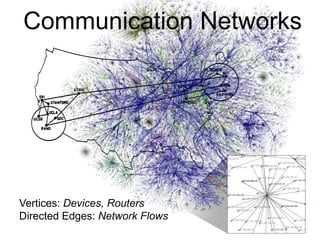
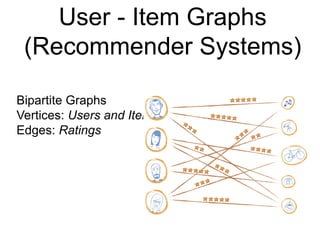
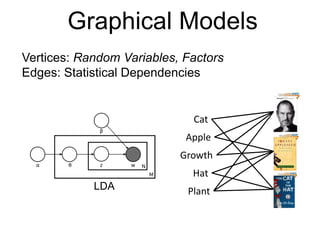
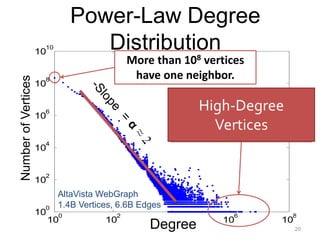
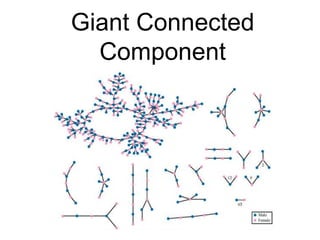
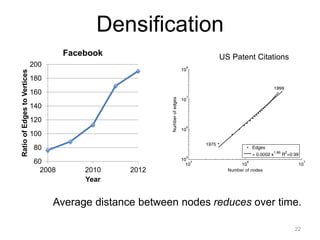
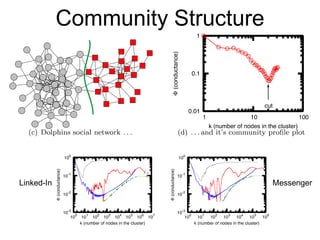
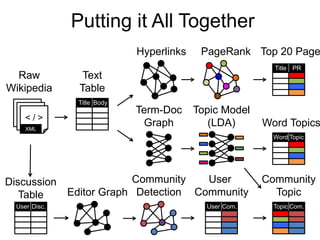
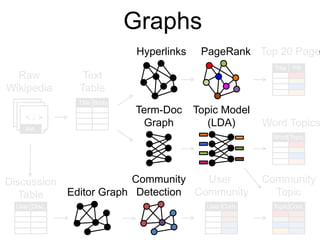
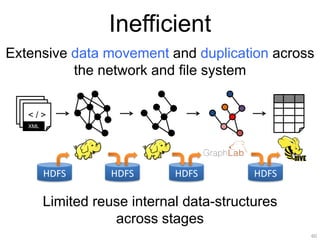
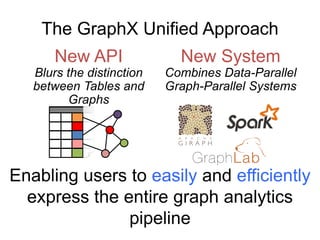
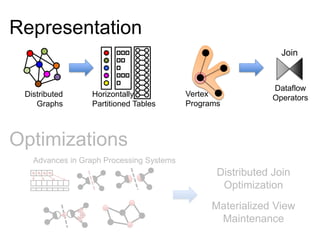
This document provides an introduction and overview of graph analytics and graph structured data. It discusses how graph data arises naturally from many real-world domains such as social networks, web graphs, and biological networks. It also outlines some common properties of graph data derived from natural phenomena, such as power-law degree distributions and community structure. Finally, it introduces common graph algorithms, graph processing systems, and the GraphX graph computation framework in Apache Spark.

1. Introduction to
Graph Analytics
CS194-16 Introduction to Data Science
*These slides are best viewed in PowerPoint with anima
Joseph E. Gonzalez
Post-doc, AMPLab
jegonzal@cs.berkeley.edu

2. Outline
1. Graph structured data
2. Common properties of graph data
3. Graph algorithms
4. Systems for large-scale graph
computation
5. GraphX: Graph Computation in Spark
6. Summary of other graph frameworks

3. Graph structured data is
everywhere …

4. Social Network
Vertices
• Users
• Posts / Images
Edges
• Social Relationships
• Directed: Twitter
• Undirected: Facebook
• Likes

5. CHAPTER 1. OVERVIE
27
15
23
10 20
4
13
16
34
31
14
12
18
17
30
33
32
9
2
1
5
6
21
24
25
3
8
22
11
7
19
28
29
26
e 1.7: From the social network of friendships in the karate club from Figure 1.1,
nd clues to the latent schism that eventually split the group into two separate clu
Actual Social Graph
Karate Club Network

6. Web Graphs
• Vertices: Web-pages
• Edges: Links (Directed)
Generated Content:
• Click-streams
Wikipedia restricted to
1000 climate change
pages

7. Web Graphs
• Vertices: Web-pages
• Edges: Links (Directed)
Generated Content:
• Click-streams
2004 Political Blogs

8. Semantic Networks
Organize Knowledge
Vertices: Subject,
Object
Edges: Predicates
Example:
Google Knowledge Graph
• 570M Vertices
• 18B Edges
http://wiki.dbpedia.org

9. Transaction Networks
Supply Chain:
Vertices: Suppliers/Consumers
Edges: Exchange of Goods
Transaction Networks (e.g., Bitcoin):
Vertices: Users
Edges: Exchange of Currency
http://anonymity-in-bitcoin.blogspot.com/2011/07/bitcoin-is-not-

10. Transaction Networks
Supply Chain:
Vertices: Suppliers/Consumers
Edges: Exchange of Goods
Transaction Networks (e.g., Bitcoin):
Vertices: Users
Edges: Exchange of Currency

11. Biological Networks
Protein-Protein Interaction Networks (Interactomes)
Vertices: Proteins
Edges: Interactions

12. Biological Networks
Regulatory Networks
(Bipartite)
Vertices: Regulators, targets
Edges: Regulates target

13. Email
Call records
Communication Networks
Vertices: Devices, Routers
Directed Edges: Network Flows

14. Who Talks to Whom
GraphEnron Email Graphs
Vertices: Users
Directed Edges: Email FromTo

15. User - Item Graphs
(Recommender Systems)
Bipartite Graphs
Vertices: Users and Items
Edges: Ratings

16. Graphical Models
Vertices: Random Variables, Factors
Edges: Statistical Dependencies
LDA
Cat
Apple
Growth
Hat
Plant

17. Co-Authorship Network
Vertices: Authors
Edges: Co-authorship
Example: Erdos
Number
http://academic.research.microsoft.com/VisualExplorer#2952384&1112639

18. Others?

19. Common properties of
graphs derived from
natural phenomena

20. Power-Law Degree
Distribution
10
0
10
2
10
4
10
6
10
810
0
10
2
10
4
10
6
10
8
10
10
degree
count
Top 1% of vertices are
adjacent to
50% of the edges!
High-Degree
Vertices
20
NumberofVertices
AltaVista WebGraph
1.4B Vertices, 6.6B Edges
Degree
More than 108 vertices
have one neighbor.

21. Giant Connected
Component

22. Densification
22
Average distance between nodes reduces over time.
60
80
100
120
140
160
180
200
2008 2010 2012
RatioofEdgestoVertices
Year
Facebook US Patent Citations

23. Community Structure
Linked-In Messenger

24. Graph Algorithms
“Think Globally, Act Locally”

25. 25
Identifying Leaders

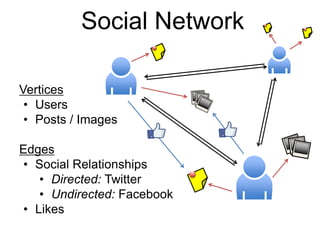
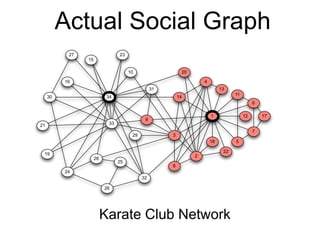
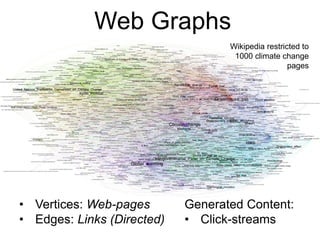
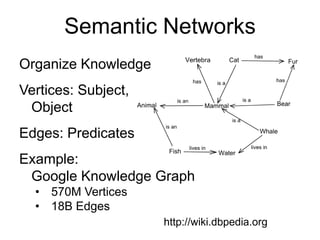
26. PageRank (Centrality
Measures)
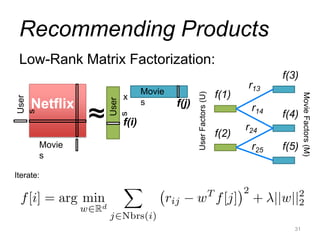
Recursive Relationship:
Where:
»α is the random reset probability (typically 0.15)
»L[j] is the number of links on page j
1 32
4 65
http://ilpubs.stanford.edu:8090/422/1/1999-66.pdf

27. Liberal Conservative
Post
Post
Post
Post
Post
Post
Post
Post
Predicting Behavior
Post
Post
Post
Post
Post
Post
Post
Post
Post
Post
Post
Post
Post
Post
?
?
?
?
?
?
?
? ?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
? ?
?
27

28. Profile
Label Propagation
(Structured Prediction)
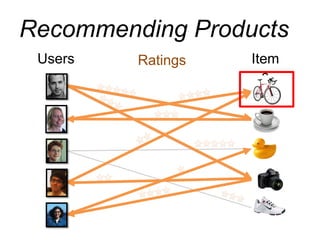
Social Arithmetic:
Recurrence Algorithm:
» iterate until convergence
Sue Ann
Carlos
Me
50% What I list on my profile
40% Sue Ann Likes
10% Carlos Like
40%
10%
50%
80% Cameras
20% Biking
30% Cameras
70% Biking
50% Cameras
50% Biking
I Like:
+
60% Cameras, 40% Biking
Likes[i]= Wij ´ Likes[ j]
jÎFriends[i]
å
http://www.cs.cmu.edu/~zhuxj/pub/CMU-CALD-02-107.pdf

29. Ratings Item
s
Recommending Products
Users

30. Low-Rank Matrix Factorization:
31
r13
r14
r24
r25
f(1)
f(2)
f(3)
f(4)
f(5)
UserFactors(U)
MovieFactors(M)
User
s
Movie
sNetflix
User
s≈
x
Movie
s
f(i)
f(j)
Iterate:
Recommending Products

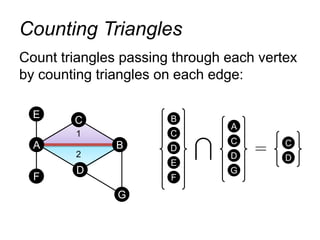
31. Count triangles passing through each
vertex:
Measure “cohesiveness” of local community
1
2 3
4
Finding Communities
ClusterCoeff[i] =
2 * #Triangles[i]
Deg[i] * (Deg[i] – 1)

32. Count triangles passing through each vertex
by counting triangles on each edge:
Counting Triangles
2
1
E
F
D
C
G
D
C
E
F
B
D
C
G
A
D
CA B

33. Every vertex starts out with a unique
component id (typically it’s vertex id):
Connected Components
4
5
6
1
3
2 4
4
4
1
2
1 4
4
4
1
1
1

34. Putting it All Together
Raw
Wikipedia
< / >< / >< / >
XML
Hyperlinks PageRank Top 20 Page
Title PR
Text
Table
Title Body
Topic Model
(LDA) Word Topics
Word Topic
Editor Graph
Community
Detection
User
Community
User Com.
Term-Doc
Graph
Discussion
Table
User Disc.
Community
Topic
Topic Com.

35. Many Other Graph Algorithms
• Collaborative Filtering
– Alternating Least Squares
– Stochastic Gradient
Descent
– Tensor Factorization
• Structured Prediction
– Loopy Belief Propagation
– Max-Product Linear
Programs
– Gibbs Sampling
• Semi-supervised ML
– Graph SSL
– CoEM
• Community Detection
– Triangle-Counting
– K-core Decomposition
– K-Truss
• Graph Analytics
– PageRank
– Personalized PageRank
– Shortest Path
– Graph Coloring
• Classification
– Neural Networks
36

36. The Graph-Parallel Pattern
37
Model / Alg.
State
Fundamental Pattern

37. Graph-Parallel Systems
38
Expose specialized APIs to simplify
graph programming.

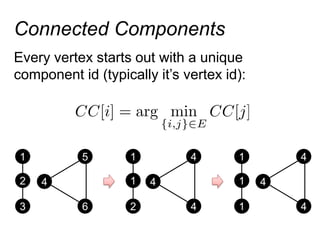
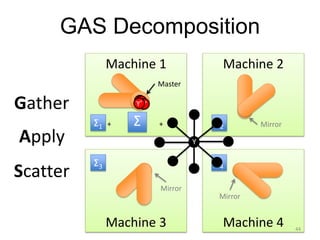
38. The Vertex Program Abstraction
Vertex-Programs interact by sending messages.
iPregel_PageRank(i, messages) :
// Receive all the messages
total = 0
foreach( msg in messages) :
total = total + msg
// Update the rank of this vertex
R[i] = 0.15 + total
// Send new messages to neighbors
foreach(j in out_neighbors[i]) :
Send msg(R[i]) to vertex j
39Malewicz et al. [PODC’09, SIGMOD’10]

39. Barrier
Iterative Bulk Synchronous
Execution
Compute Communicate

40. Graph-Parallel Systems
41
Exploit graph structure to achieve
orders-of-magnitude performance gains
over more general data-parallel
systems.

41. Graph System
Optimizations
42
Specialized
Data-Structures
Vertex-Cuts
Partitioning
Remote
Caching / Mirroring
Message
Combiners
Active Set Tracking

42. Machine 1 Machine 2
Split High-Degree vertices
New Abstraction  Equivalence on Split 43
Program
This
Run on This

43. Machine 2Machine 1
Machine 4Machine 3
GAS Decomposition
Σ1 Σ2
Σ3 Σ4
+ + +
YYYY
Y’
Σ
Y’Y’Y’Gather
Apply
Scatter
44
Master
Mirror
Mirror
Mirror

44. 2D Partitioning
Adj.
Matrix
Vertices
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
Vertices
16 Machines
vi
vi
2
5 6 7 8
10
14
vi only has
neighbors on
7 machines
45

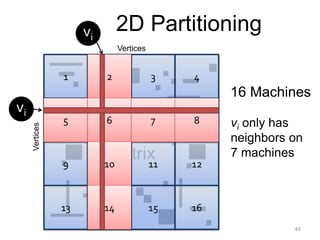
45. Counted: 34.8 Billion
Triangles
50
Triangle Counting on Twitter
64 Machines
15 Seconds
1536 Machines
423 Minutes
Hadoop
[WWW’11]
S. Suri and S. Vassilvitskii, “Counting triangles and the curse of the last reducer,” WWW’11
1000 x
Faster
40M Users, 1.4 Billion Links

46. Break!
jegonzal@eecs.berkeley.edu
http://tinyurl.com/ampgraphx

47. Graph Analytics Pipeline
Raw
Wikipedia
< / >< / >< / >
XML
Hyperlinks PageRank Top 20 Page
Title PR
Text
Table
Title Body
Topic Model
(LDA) Word Topics
Word Topic
Editor Graph
Community
Detection
User
Community
User Com.
Term-Doc
Graph
Discussion
Table
User Disc.
Community
Topic
Topic Com.

48. Tables
Raw
Wikipedia
< / >< / >< / >
XML
Hyperlinks PageRank Top 20 Page
Title PR
Text
Table
Title Body
Topic Model
(LDA) Word Topics
Word Topic
Editor Graph
Community
Detection
User
Community
User Com.
Term-Doc
Graph
Discussion
Table
User Disc.
Community
Topic
Topic Com.

49. Graphs
Raw
Wikipedia
< / >< / >< / >
XML
Hyperlinks PageRank Top 20 Page
Title PR
Text
Table
Title Body
Topic Model
(LDA) Word Topics
Word Topic
Editor Graph
Community
Detection
User
Community
User Com.
Term-Doc
Graph
Discussion
Table
User Disc.
Community
Topic
Topic Com.

50. Separate Systems
Tables Graphs

51. Separate Systems
Graphs
Dataflow Systems
Table
Resul
t
Row
Row
Row
Row

52. Separate Systems
Dataflow Systems Graph Systems
Dependency
Graph
Table
Resul
t
Row
Row
Row
Row

53. Separate systems
for each view can be
difficult to use and
inefficient
58

54. Difficult to Program and Use
Users must Learn, Deploy, and
Manage multiple systems
Leads to brittle and often
complex interfaces
59

55. Inefficient
60
Extensive data movement and duplication across
the network and file system
< / >< / >< / >
XML
HDFS HDFS HDFS HDFS
Limited reuse internal data-structures
across stages

56. The GraphX Unified Approach
Enabling users to easily and efficiently
express the entire graph analytics
pipeline
New API
Blurs the distinction
between Tables and
Graphs
New System
Combines Data-Parallel
Graph-Parallel Systems

57. Representation
Optimizations
Distributed
Graphs
Horizontally
Partitioned Tables
Join
Vertex
Programs
Dataflow
Operators
Advances in Graph Processing Systems
Distributed Join
Optimization
Materialized View
Maintenance

58. View a Graph as a Table
Id
Rxin
Jegonzal
Franklin
Istoica
SrcId DstId
rxin jegonzal
franklin rxin
istoica franklin
franklin jegonzal
Property (E)
Friend
Advisor
Coworker
PI
Property (V)
(Stu., Berk.)
(PstDoc, Berk.)
(Prof., Berk)
(Prof., Berk)
R
J
F
I
Property Graph
Vertex Property Table
Edge Property Table

59. Spark Table Operators
Table (RDD) operators are inherited from
Spark:
64
map
filter
groupBy
sort
union
join
leftOuterJoin
rightOuterJoin
reduce
count
fold
reduceByKey
groupByKey
cogroup
cross
zip
sample
take
first
partitionBy
mapWith
pipe
save
...

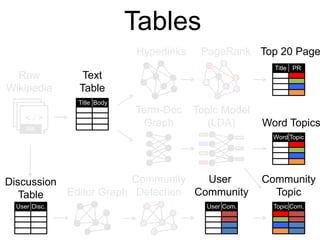
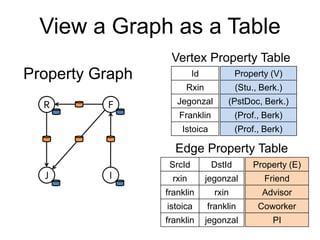
60. class Graph [ V, E ] {
def Graph(vertices: Table[ (Id, V) ],
edges: Table[ (Id, Id, E) ])
// Table Views -----------------
def vertices: Table[ (Id, V) ]
def edges: Table[ (Id, Id, E) ]
def triplets: Table [ ((Id, V), (Id, V), E) ]
// Transformations ------------------------------
def reverse: Graph[V, E]
def subgraph(pV: (Id, V) => Boolean,
pE: Edge[V,E] => Boolean): Graph[V,E]
def mapV(m: (Id, V) => T ): Graph[T,E]
def mapE(m: Edge[V,E] => T ): Graph[V,T]
// Joins ----------------------------------------
def joinV(tbl: Table [(Id, T)]): Graph[(V, T), E ]
def joinE(tbl: Table [(Id, Id, T)]): Graph[V, (E, T)]
// Computation ----------------------------------
def mrTriplets(mapF: (Edge[V,E]) => List[(Id, T)],
reduceF: (T, T) => T): Graph[T, E]
}
Graph Operators (Scala)
65

61. class Graph [ V, E ] {
def Graph(vertices: Table[ (Id, V) ],
edges: Table[ (Id, Id, E) ])
// Table Views -----------------
def vertices: Table[ (Id, V) ]
def edges: Table[ (Id, Id, E) ]
def triplets: Table [ ((Id, V), (Id, V), E) ]
// Transformations ------------------------------
def reverse: Graph[V, E]
def subgraph(pV: (Id, V) => Boolean,
pE: Edge[V,E] => Boolean): Graph[V,E]
def mapV(m: (Id, V) => T ): Graph[T,E]
def mapE(m: Edge[V,E] => T ): Graph[V,T]
// Joins ----------------------------------------
def joinV(tbl: Table [(Id, T)]): Graph[(V, T), E ]
def joinE(tbl: Table [(Id, Id, T)]): Graph[V, (E, T)]
// Computation ----------------------------------
def mrTriplets(mapF: (Edge[V,E]) => List[(Id, T)],
reduceF: (T, T) => T): Graph[T, E]
}
Graph Operators (Scala)
66
def mrTriplets(mapF: (Edge[V,E]) => List[(Id, T)],
reduceF: (T, T) => T): Graph[T, E]
capture the Gather-Scatter pattern from
specialized graph-processing systems

62. Triplets Join Vertices and
Edges
The triplets operator joins vertices and
edges:
TripletsVertices
B
A
C
D
Edges
A B
A C
B C
C D
A BA
B A C
B C
C D

63. Map-Reduce Triplets
Map-Reduce triplets collects information
about the neighborhood of each vertex:
C D
A C
B C
A B
Src. or Dst.
MapFunction( )  (B, )
MapFunction( )  (C, )
MapFunction( )  (C, )
MapFunction( )  (D, )
Reduce
(B, )
(C, + )
(D, )
Message
Combiners

64. Using these basic GraphX operators
we implemented Pregel and GraphLab
in under 50 lines of code!
69

65. The GraphX Stack
(Lines of Code)
GraphX (2,500)
Spark (30,000)
Pregel API (34)
PageRank
(20)
Connected
Comp. (20)
K-core
(60)
Triangl
e
Count
(50)
LDA
(220)
SVD++
(110)
Some algorithms are more naturally expressed
using the GraphX primitive operators

66. We express enhanced Pregel and
GraphLab
abstractions using the GraphX operators
in less than 50 lines of code!
71

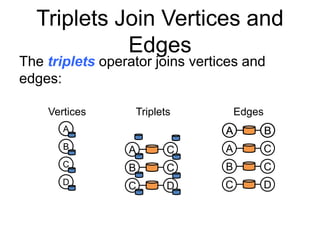
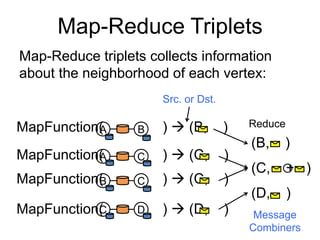
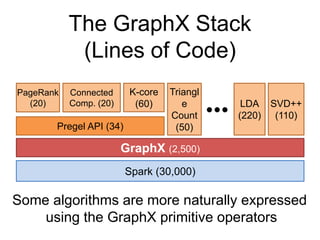
67. Enhanced Pregel in GraphX
72Malewicz et al. [PODC’09, SIGMOD’10]
pregelPR(i, messageList ):
// Receive all the messages
total = 0
foreach( msg in messageList) :
total = total + msg
// Update the rank of this vertex
R[i] = 0.15 + total
// Send new messages to neighbors
foreach(j in out_neighbors[i]) :
Send msg(R[i]/E[i,j]) to vertex
Require Message
CombinersmessageSum
messageSum
Remove Message
Computation
from the
Vertex Program
sendMsg(ij, R[i], R[j], E[i,j]):
// Compute single message
return msg(R[i]/E[i,j])
combineMsg(a, b):
// Compute sum of two messages
return a + b

68. GraphX System Design

69. Part. 2
Part. 1
Vertex
Table
(RDD)
B C
A D
F E
A D
Distributed Graphs as Tables
(RDDs)
D
Property Graph
B C
D
E
AA
F
Edge
Table
(RDD)A B
A C
C D
B C
A E
A F
E F
E D
B
C
D
E
A
F
Routing
Table
(RDD)
B
C
D
E
A
F
1
2
1 2
1 2
1
2
2D Vertex Cut Heuristic

70. Vertex
Table
(RDD)
Caching for Iterative mrTriplets
Edge Table
(RDD)
A B
A C
C D
B C
A E
A F
E F
E D
Mirror
Cache
B
C
D
A
Mirror
Cache
D
E
F
A
B
C
D
E
A
F
B
C
D
E
A
F
A
D

71. Vertex
Table
(RDD)
Edge Table
(RDD)
A B
A C
C D
B C
A E
A F
E F
E D
Mirror
Cache
B
C
D
A
Mirror
Cache
D
E
F
A
Incremental Updates for Iterative
mrTriplets
B
C
D
E
A
F
Change AA
Change E
Scan

72. Vertex
Table
(RDD)
Edge Table
(RDD)
A B
A C
C D
B C
A E
A F
E F
E D
Mirror
Cache
B
C
D
A
Mirror
Cache
D
E
F
A
Aggregation for Iterative mrTriplets
B
C
D
E
A
F
Change
Change
Scan
Change
Change
Change
Change
Local
Aggregate
Local
Aggregate
B
C
D
F

73. Performance Comparisons
22
68
207
354
1340
0 200 400 600 800 1000 1200 1400 1600
GraphLab
GraphX
Giraph
Naïve Spark
Mahout/Hadoop
Runtime (in seconds, PageRank for 10 iterations)
GraphX is roughly 3x slower than GraphLab
Live-Journal: 69 Million Edges

74. GraphX scales to larger
graphs
203
451
749
0 200 400 600 800
GraphLab
GraphX
Giraph
Runtime (in seconds, PageRank for 10 iterations)
GraphX is roughly 2x slower than GraphLab
»Scala + Java overhead: Lambdas, GC time, …
»No shared memory parallelism: 2x increase in comm.
Twitter Graph: 1.5 Billion Edges

75. PageRank is just one
stage….
What about a pipeline?

76. HDFSHDFS
ComputeSpark Preprocess Spark Post.
A Small Pipeline in GraphX
Timed end-to-end GraphX is faster than
Raw Wikipedia
< / >< / >< / >
XML
Hyperlinks PageRank Top 20 Pages
342
1492
0 200 400 600 800 1000 1200 1400 1600
GraphLab + Spark
GraphX
Giraph + Spark
Spark
Total Runtime (in Seconds)
605
375

77. Open Source Project
Alpha release since Spark 0.9
Contributors? Python Bindings?

78. Graph Processing Systems
• Apache Giraph: java Pregel
implementation
• GraphLab.org: C++ GraphLab
implementation
• NetworkX: python API for small gaphs
• GraphLab Create: commercial GraphLab
python framework for large graphs and
ML
• Gephi: graph visualization framework

79. Graph Database
Technologies
Property graph data-model for storing and
retrieving graph structured data.
• Neo4j: popular commercial graph
database
• Titan: open-source distributed graph
database

80. Break!
jegonzal@eecs.berkeley.edu
http://tinyurl.com/ampgraphx

81. About Scala
High-level language for the Java VM
»Object-oriented + functional programming
Statically typed
»Comparable in speed to Java
»But often no need to write types due to type
inference
Interoperates with Java
»Can use any Java class, inherit from it, etc; can
also call Scala code from Java

82. Quick Tour
Declaring variables:
var x: Int = 7
var x = 7 // type inferred
val y = “hi” // read-only
Java equivalent:
int x = 7;
final String y = “hi”;
Functions:
def square(x: Int): Int = x*x
def min(a:Int, b:Int): Int = {
if (a < b) a else b
}
def announce(text: String) {
println(text)
}
Java equivalent:
int square(int x) {
return x*x;
}
void announce(String text) {
System.out.println(text);
}

83. Quick Tour
Generic types:
var arr = new Array[Int](8)
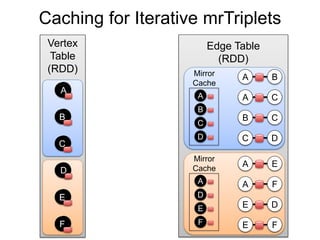
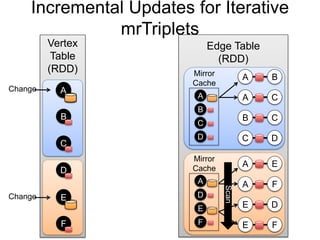
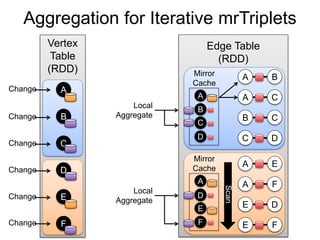
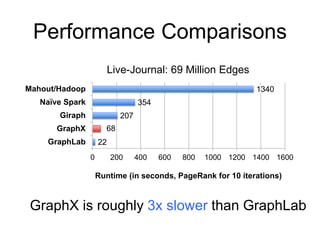
var lst = List(1, 2, 3)
// type of lst is List[Int]
Java equivalent:
int[] arr = new int[8];
List<Integer> lst =
new ArrayList<Integer>();
lst.add(...)
Indexing:
arr(5) = 7
println(lst(5))
Java equivalent:
arr[5] = 7;
System.out.println(lst.get(5));

84. Processing collections with functional
programming:
val list = List(1, 2, 3)
list.foreach(x => println(x)) // prints 1, 2, 3
list.foreach(println) // same
list.map(x => x + 2) // => List(3, 4, 5)
list.map(_ + 2) // same, with placeholder notation
list.filter(x => x % 2 == 1) // => List(1, 3)
list.filter(_ % 2 == 1) // => List(1, 3)
list.reduce((x, y) => x + y) // => 6
list.reduce(_ + _) // => 6
QuickTour
Function expression (closure)
All of these leave the list unchanged (List is immutable)

85. Other Collection Methods
Scala collections provide many other
functional methods; for example, Google for
“Scala Seq”Method on Seq[T] Explanation
map(f: T => U): Seq[U] Pass each element through f
flatMap(f: T => Seq[U]): Seq[U] One-to-many map
filter(f: T => Boolean): Seq[T] Keep elements passing f
exists(f: T => Boolean): Boolean True if one element passes
forall(f: T => Boolean): Boolean True if all elements pass
reduce(f: (T, T) => T): T Merge elements using f
groupBy(f: T => K): Map[K,List[T]] Group elements by f(element)
sortBy(f: T => K): Seq[T] Sort elements by f(element)
. . .