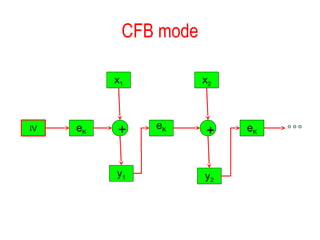
The document discusses various cryptographic techniques including: - Block ciphers like the Shift Cipher, Substitution Cipher, Affine Cipher, Vigenere Cipher, Hill Cipher, and Permutation Cipher. - Stream ciphers like the Linear Feedback Shift Register (LFSR) cipher. - Public key cryptography techniques including RSA, Rabin, and the Digital Signature Algorithm (DSA). - Modes of operation for block ciphers like Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), and Output Feedback (OFB).

1. Computer Security
Basic Crypto

2. Introduction
Cryptosystem: (E,D,M,K,C)
M is the set of plaintexts
K the set of keys
C the set of ciphertexts
E: M × K→ C the set of enciphering
functions
D: C × K→ M the set of deciphering
functions

3. Introduction
• Shift Cipher: M = C = K = Z26, with
-- eK(x) = x + K mod26
-- dK(y) = y – K mod26
where x,y is in Z26
• Substitution Cipher: P = C = Z26, with K
the set of permutations π on Z26 and
-- eπ(x) = π(x)
-- dπ(y) = π-1
(y).

4. Cryptosystems
Block ciphers
The Shift Cipher and Substitution Cipher are block
ciphers: successive plaintext elements (blocks) are
encrypted using the same key.
We now consider some other block ciphers.
• The Affine Cipher, is a special case of the
• Substitution Cipher with
• -- eK(x) = ax + b mod26
-- dK(y) = a-1
y - a-1
b mod26
where a,b x,y is in Z26 and x is invertible.

5. Block ciphers
The Vigenere Cipher is polyalphabetic.
Let m > 1
• M = C = K = (Z26)m
• For a key K = (k1, …, km)
• -- eK(x1,…,xm) = (x1 + k1, …, xm + km)
-- dK(y1,…,ym) = (y1 - k1, …, ym - km)
where all operations are in Z26.

6. Block ciphers
The Hill Cipher is also polyalphabetic.
Let m > 1
• M = C = (Z26)m
, K is the set of all m by m
invertible matrices over (Z26)m
• For a key K
• -- eK(x) = xK
-- dK(y)= yK-1
with all operations are in Z26.

7. Block ciphers
The Permutation Cipher. Let m > 1
M = C = (Z26)m
,
K is the set of all permutations of {1,…,m}.
• For a key (permutation) π
• -- eπ(x1,…,xm) = (xπ(1),…, xπ(m))
-- dπ(y1,…,ym) = (yπ−1(1),…, yπ−1(1))
where π−1
(1) is the inverse of π.

8. Stream Ciphers
The ciphers considered so far are block ciphers.
Another type of cryptosystem is the stream cipher.

9. Stream Ciphers
• A synchronous stream cipher is a tuple (E,D,M,C,K,L,)
with a function g such that:
• M, C, K, E, D are as before.
• L is the keysteam alphabet
• g is the keystream generator: it takes as input a key K
and outputs an infinite string
z1,z2, …
called the keystream, where zi are in L.
• For each ziare in L there is an encryption rule ez in E,
and a decryption rule dz in D such that:
dz (ez(x)) = x
for all plaintexts x in M.

10. Stream Ciphers
The Linear Feedback Shift Register or LFSR.
The keystream is computed as follows:
Let (k1,k2, … ,km) be the initialized key vector at
time t.
At the next time unit the key vector is updated as
follows:
-- k1 is tapped as the next keystream bit
-- k2, … , km are each shifted one place to the left
-- the “new” value of km is computed by
m-1
km+1 = Σcjkj+1
j=0

11. Stream Ciphers
Let x1,x2, … be the plaintext (a binary string).
Then the ciphertext is:
y1,y2, …
where yi,= xi+ ki, for i=1,2,… and the sum
is bitwise xor .

12. Cryptanalysis
Attacks on Cryptosystems
• Ciphertext only attack: the opponent possesses
a string of ciphertexts: y1,y2, …
• Known plaintext attack: the opponent
possesses a string of plaintexts x1,x2, … and the
corresponding string of ciphertexts: y1,y2, …

13. Attacks on Cryptosystems
• Chosen plaintext attack: the opponent can
choose a string of plaintexts x1,x2, … and
obtain the corresponding string of
ciphertexts: y1,y2, …
• Chosen ciphertext attack: the opponent can
choose a string of ciphertexts: y1,y2, … and
construct the corresponding string of
plaintexts x1,x2, …

14. Cryptanalysis
• Cryptanalysis of the shift cipher and substitution cipher:
Ciphertext attack -- use statistical properties of the
language
• Cryptanalysis of the affine and Vigenere cipher:
Ciphertext attack -- use statistical: properties of the
language
• Attacks on the affine and Vigenere cipher:
Ciphertext attack -- use statistical: properties of the
language

15. Cryptanalysis
• Cryptanalysis of the Hill cipher:
Known plaintext attack
• Cryptanalysis of the LFSR stream cipher:
Known plaintext attack

16. One time pad
This is a binary stream cipher whose key
stream is a random stream
This cipher has perfect secrecy

17. Security
• Computational security
Computationally hard to break: requires super-
polynomial computations (in the length of the
ciphertext)
• Provable security
Security is reduced to a well studied problem
though to be hard, e.g. factorization.
• Unconditional security
No bound on computation: cannot be broken even
with infinite power/space.
Only way to break is by “lucky” guessing.

18. Some Probability Theory
• The random variables X,Y are independent
if:
Pr[x,y] = Pr[x] . Pr[y], for all x,y in X
In general,
Pr[x,y] = Pr[x|y] . Pr[y]
= Pr[y|x] . Pr[x], for all x,y in X

19. Some Probability Theory
• Bayes’ Law:
Pr[x|y] =
• Corollary:
X,Y are independent random variables (r.v.)
iff
Pr[x|y] = Pr[x] for all x,y in X
Pr[y]
Pr[y|x] . Pr[x]
---------------- for all x,y in X

20. Perfect secrecy
• A cryptosystem is perfectly secure if :
Pr[x|y] = Pr[x],
for all x in M and y in C

21. Perfect secrecy
Theorem
Let |K|=|C|=|M| for a cryptosystem.
We have perfect secrecy iff :
• Every key is used with equal probability,
• For each x in P and y in C there is a unique key K
in K that encrypts x to y
1
|K |
------

22. One time pad
We have K = C = M = Z2
n
.
Also given:
x = x1,…,xn and y = y1,…,yn,
the key K = K1,…,Kn is unique because K = x+y mod 2
Finally all keys are chosen equiprobably.
Therefore,
the one time pad has perfect secrecy

23. Kerchoffs’ assumption
The adversary knows all details of the
encrypting function except the secret key

24. DES
DES is a Feistel cipher.
Block length 64 bits (effectively 56)
Key length 56 bits
Ciphertext length 64 bits

25. DES
It has a round function g for which:
g([Li-1
,Ri-1
]),Ki
) = (Li
,Ri
),
where
Li
= Ri-1
and Ri
= Li-1
XOR f (Ri-1
, Ki
).

26. DES round encryption

27. DES inner function

28. DES computation path

29. Attacks on DES
• Brute force
• Linear Cryptanalysis
-- Known plaintext attack
• Differential cryptanalysis
– Chosen plaintext attack
– Modify plaintext bits, observe change in
ciphertext
No dramatic improvement on brute force

30. Countering Attacks
• Large keyspace combats brute force attack
• Triple DES (say EDE mode, 2 or 3 keys)
• Use AES

31. AES
Block length 128 bits.
Key lengths 128 (or 192 or 256).
The AES is an iterated cipher with Nr=10 (or 12 or 14)
In each round we have:
• Subkey mixing
• A substitution
• A permutation

32. Modes of operation
Four basic modes of operation are available for
block ciphers:
• Electronic codebook mode: ECB
• Cipher block chaining mode: CBC
• Cipher feedback mode: CFB
• Output feedback mode: OFB

33. Electronic Codebook mode, ECB
Each plaintext xi is encrypted with the same key K:
yi = eK(xi).
So, the naïve use of a block cipher.

34. ECB
x1 x2 x3 x4
y4y3y2y1
DES DES DES DES

35. Cipher Block Chaining mode, CBC
Each cipher block yi-1 is xor-ed with the next plaintext xi :
yi = eK(yi-1XOR xi)
before being encrypted to get the next plaintext yi.
The chain is initialized with
an initialization vector: y0 = IV
with length, the block size.

36. CBC
x1
+ + ++
IV
x2 x3 x4
y4y3y2y1
DES DES DES DES

37. Cipher and Output feedback
modes (CFB & OFB)
CFB
z0 = IV and recursively:
zi = eK(yi-1) and yi = xiXOR zi
OFB
z0 = IV and recursively:
zi = eK(zi-1) and yi = xiXOR zi

38. CFB mode
IV eK
eK
y1
+
x1
eK
x2
y2
+

39. OFB mode
IV eK
eK
y1
+
x1 x2
y2
+

40. Public Key Cryptography
Alice Bob
Alice and Bob want to exchange a private key in public.

41. Public Key Cryptography
Alice ga
mod p Bob
gb
mod p
The private key is: gab
mod p
where p is a prime and g is a generator of Zp

42. The RSA cryptosystem
Let n = pq, where p and q are primes.
Let M = C = Zn, and let
a,b be such that ab = 1 mod φ(n).
Define
eK(x) = xb
mod n
and
dK(y) = ya
mod n,
where (x,y)ε Zn.
Public key = (n,b), Private key (n,a).

43. Check
We have: ed = 1 mod φ(n), so ed = 1 + tφ(n).
Therefore,
dK(eK(m)) = (me
)d
= med
= mtφ(n)+1
= (mφ(n)
)t
m = 1.m = m mod n

44. Example
p = 101, q = 113, n = 11413.
φ(n) = 100x112 = 11200 = 26
52
7
For encryption use e = 3533.
Then d = e-1
mod11200 = 6597.
Bob publishes: n = 11413, e = 3533.
Suppose Alice wants to encrypt: 9726.
She computes 97263533
mod 11413 = 5761
To decrypt it Bob computes:
57616597
mod 11413 = 9726

45. Security of RSA
1. Relation to factoring.
Recovering the plaintext m from an RSA ciphertext c is
easy if factoring is possible.
2. The RSA problem
Given (n,e) and c, compute: m such that me
= c mod n

46. The Rabin cryptosystem
Let n = pq, p,q primes with p,q 3 mod 4. Let P = C = Zn*
and define K = {(n,p,q)}.
For K = (n,p,q) define
eK(x) = x 2
mod n
dK(y) = mod n
The value of n is the public key, while p,q are the private key.
≡
y

47. The RSA digital signature scheme
Let n = pq, where p and q are primes.
Let P = A = Zn, and define
e,d such that ed = 1 mod φ(n).
Define
sigK(m) = md
mod n
and
verK(m,y) = true y = me
mod n,
where (m,y)εZn.
Public key = (n,e), Private key (n,d).
⇔

48. The Digital Signature Algorithm
Let p be a an L-bit prime prime,
512 ≤ L ≤ 1024 and L ≡ 0 mod 64 ,
let q be a 160-bit prime that divides p-1 and
Let α ε Zp
*
be a q-th root of 1 modulo p.
Let M = Zp-1,
A = Zqx Zq and
K = {(x,y): y = αx
modp }.
• The public key is p,q,α,y.
• The private key is (p,q,α), x.

49. The Digital Signature scheme
• Signing
Let m ε Zp-1 be a message.
For public key is p,g,α,y, with y = αx
modp, and
secret random number k ε Zp-1, define: sigK(m,k) = (s,t), where
– s = (αk
modp) mod q
– t = (SHA1(m)+xs)k-1
modq
• Verification
Let
– e1 = SHA-1(m) t-1
modq
– e2 = st-1
modq
verK(m,(s,t)) = true (αe1
ye2
modp) mod q = s.
⇔