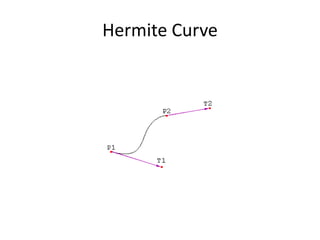
This document provides information on geometric modeling and different curve representation methods. It discusses that a curve can be represented mathematically, explicitly, implicitly, or parametrically. It also outlines different geometric modeling methods like wireframe, surface, and solid modeling. The document then focuses on Hermite curves, describing them as cubic polynomials defined by function and derivative values at endpoints, making them smooth and continuous. Hermite curves are commonly used in computer graphics to interpolate between key points.

1. UNIT II - GEOMETRIC MODELING
Representation of a curve:
• Mathematically, curve is a continuous map from one dimensional
space to n – dimensional shape.
• A curve is infinitely a large set of points.
• Any point have two neighbour points except for a small number of
points which have one neighbour (End points )
• There will be no end points for closed ones.
• Free form curve takes any shape and much harder to describe

2. • Mathematical Representation of a curve:
A curve or a surface may be described or
represented by a set of equations.
Three ways to describe curve are
a) Explicit( One variable is dependent on other
variable)
b) Implicit (A set of points for which equation is
true)
c) Parametric curve

4. Methods of Geometric Modelling
1. Wireframe modelling
2. Surface modelling
3. Solid modelling.
Wireframe modelling:
Wireframe is a solid shape in the form of
lines,edges and points.
Surface modelling:
Used to represent complex objects that cannot be
represented by wireframe modelling. It provides more and
less ambiguous representation.
Solid Modelling:
It provides the complete information of the object
when compared to surface modelling. It stores the geometric
data and topological information of the object.

5. • Hermite curve
• A Hermite curve is a spline where every piece is a third degree polynomial
(cubic polynomials) defined in Hermite form: that is, by its values and
initial derivatives at the end points of the equivalent domain interval.
• Cubic Hermite splines are normally used for interpolation of numeric
values defined at certain dispute values x1,x2,x3, ….., xn, to achieve a
smooth continuous function.
• The data should have the preferred function value and derivative at each
Xk. The Hermite formula is used to every interval (Xk, Xk+1) individually.
The resulting spline become continuous and will have first derivative (tells
the direction of function whether increasing or decreasing).

6. • Cubic polynomial splines are specially used in computer geometric
modeling to attain curves that pass via defined points of the plane in 3D
space. In these purposes, each coordinate of the plane is individually
interpolated by a cubic spline function of a divided parameter‘t’.
• Cubic splines can be completed to functions of different parameters, in
several ways. Bicubic splines are frequently used to interpolate data on a
common rectangular grid, such as pixel values in a digital picture. Bicubic
surface patches are an necessary tool in computer graphics.
• Hermite curves are simple to calculate but also more powerful.
• They are used to well interpolate between key points.

7. Hermite Curve