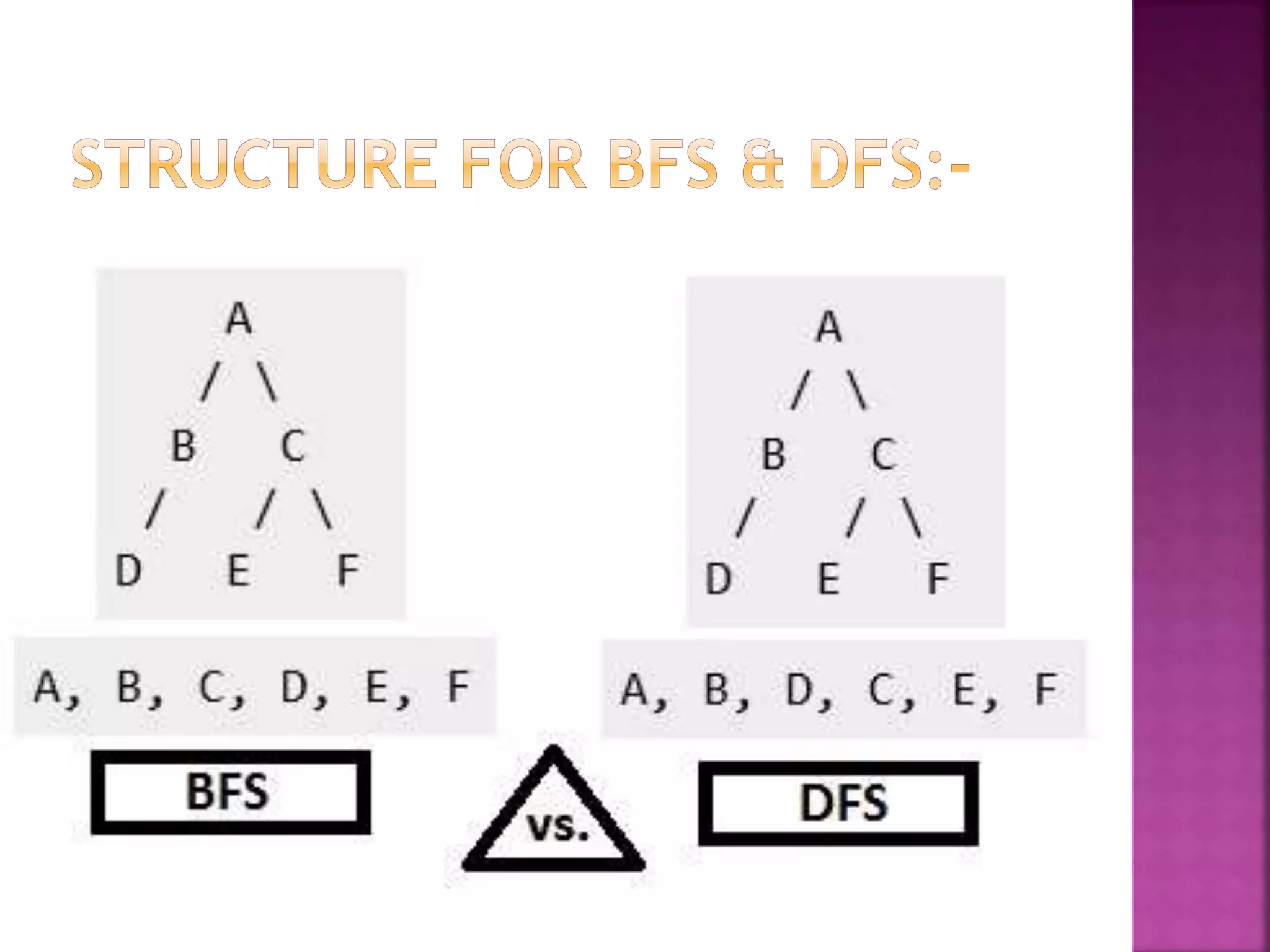
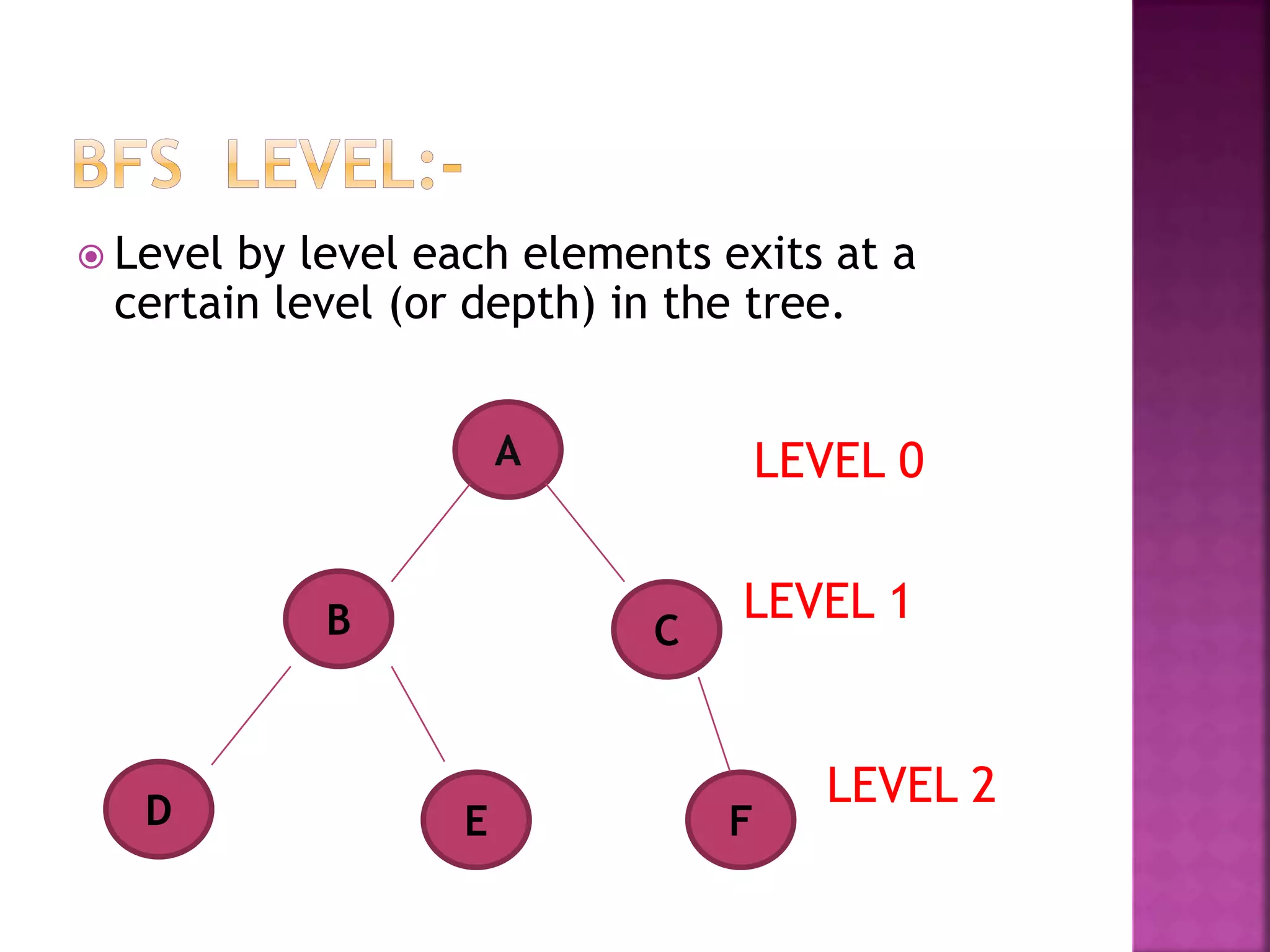
Breadth-first search (BFS) and depth-first search (DFS) are two standard graph traversal algorithms. BFS explores nodes level-by-level starting from the root node, using a queue data structure. In contrast, DFS prioritizes exploring nodes to the deepest levels first, using a stack data structure. Both algorithms are useful for problems like finding the shortest path in a graph and determining connected components. BFS and DFS can be used to generate spanning trees and forests that connect all nodes within each component of the graph.

1. BY
SAKTHIPRIYA

2. Many graph algorithm of a graph G
Require one to systematically examine
the nodes and edges of a graph G.
 There are two standard ways of graph
traversal::-
Breadth first search
Depth first search

3. During execution of our algorithm each
node N of G will be one of three
states,called status of N.
Status=1(ready state)the initial of node
n.
Status=2(waiting state)the node n is on
the queue or stack wait to be processed.
Status=3(processed state)the node n has
been processed.

4.  Breadth first search is an algorithm for
traversing or searching tree or graph data
structure.
It uses the opposite strategy depth first
traversal.
The bft another name is called “breadth
first search “

5. BFS instead explores the highest depth
node first before being forced to
backtrack and expand shallower nodes.
It is an important graph search algorithm
is used to solve many problems including
finding the shortest plan in a graph.
BFS always used in “queue”

6.  Breadth-first search (BFS) is an algorithm for
traversing or searching tree or graph data
structures.
 It uses the opposite strategy as depth-
first search, which instead explores the
highest-depth nodes first before being forced
to backtrack and expand shallower nodes.

7. Gain access to
visit the nodes.
Two operation

9.  Level by level each elements exits at a
certain level (or depth) in the tree.
LEVEL 1
LEVEL 2
A
B C
D E F
LEVEL 0

10.  Depth-first search (DFS)is a general
technique for traversing a graph
 DFS always used in “stack”
 we have inserting elements and deleting the
elements .It is used to the operation in push
and pop.
A DFS traversal of a graph G
Visits all the vertices and edges of G
Determines whether G is connected
Computes the connected components of G
Computes a spanning forest of G

11.  A subgraph S of a graph G is a graph such
that
 The vertices of S are a subset
of the vertices of G
 The edges of S are a subset
of the edges of G
 A spanning subgraph of G is a subgraph that
contains all the vertices of G

12.  A spanning tree of a connected graph is a
spanning subgraph that is a tree
 A spanning tree is not unique unless the
graph is a tree
 Spanning trees have applications to the
design of communication networks
 A spanning forest of a graph is a spanning
subgraph that is a forest

13.  A graph is connected if there is a path
between every pair of vertices
 A connected component of a graph G is a
maximal connected subgraph of G

15. Property 1
DFS(G, v) visits all the vertices and
edges in the connected component of v
Property 2
The discovery edges labeled by DFS(G, v)
form a spanning tree of the connected
component of v