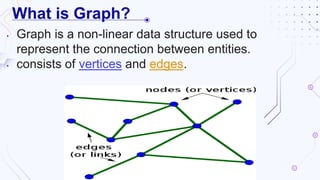
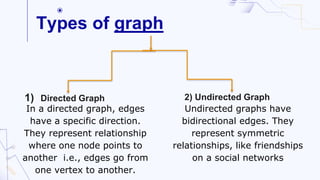
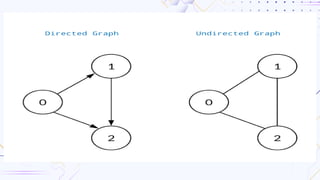
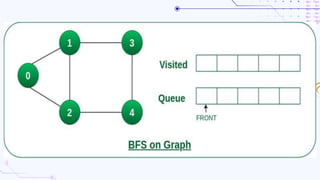
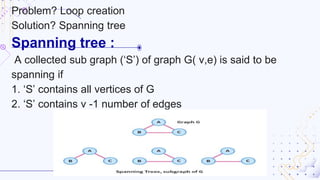
Graphs are non-linear data structures composed of vertices and edges used to represent connections between entities, with types including directed, undirected, and weighted graphs. Key algorithms for graph traversal include Depth-First Search (DFS) and Breadth-First Search (BFS), while Dijkstra's algorithm is utilized for finding the shortest path and Kruskal's and Prim's algorithms are used to create minimal cost spanning trees. Graphs have various real-life applications, such as in network design and mapping services.

1. Graph & it’s
Algorithms

2. What is Graph?
• Graph is a non-linear data structure used to
represent the connection between entities.
• consists of vertices and edges.

3. Types of graph
1) Directed Graph
In a directed graph, edges
have a specific direction.
They represent relationship
where one node points to
another i.e., edges go from
one vertex to another.
2) Undirected Graph
Undirected graphs have
bidirectional edges. They
represent symmetric
relationships, like friendships
on a social networks

5. Weighted graph
A weight graph is a graph whose edges have
a “weight” or “cost”. The weight of an edge
can represent distance, time, or anything
that models the “connection” between the
pair of nodes it connects.
For example, in the weighted graph below you
can see a blue number next to each edge.
This number is used to represent the weight
of the corresponding edge.

6. Depth-first Search
Depth-first search is an algorithm for traversing or
searching tree or graph data structures. The algorithm
starts at the root node (selecting some arbitrary node
as the root node in the case of a graph) and explores
as far as possible along each branch before
backtracking.
• Stack data structure is used in DFS.
• Null Stack(after popping values while backtracking) is
the indication to stop traversing.

8. Breadth-first Search
Also known as level-order traversal.
Starting from the root, all the nodes at a particular level
are visited first and then the nodes of the next level are
traversed till all the nodes are visited.
To do this a queue is used. All the adjacent unvisited
nodes of the current level are pushed into the queue and
the nodes of the current level are marked visited and
popped from the queue.

10. Dijkstra’s Algorithm:
( Single source shortest path )
● Usage : telephone networks , Google
maps etc
● heart of algorithm : ( Relaxation)
if d(u) + c( u,v) < d(u)
set d(u) = d(u) + c (u,v)

11. Problem? Loop creation
Solution? Spanning tree
Spanning tree :
A collected sub graph (‘S’) of graph G( v,e) is said to be
spanning if
1. ‘S’ contains all vertices of G
2. ‘S’ contains v -1 number of edges

12. Kruskal’s algorithm:
To find minimal cost spanning tree.
MST :
it is used to design efficient network with minimal cost.
Procedure :
1. Take one by one edge with lowest cost.
2. Add in spanning tree.
3. Cycle shouldn’t be created.
note : output is connected tree but in between processing
vertices could be isolated.

13. Prims algorithm:
● To construct MST.
● Number of edges= number of vertices -1.
Procedure
1. Start from a vertex.
2. Check how many vertices are connected to it.
3. Select the one with minimal cost.
NOTE :
Output will be a connected spanning tree at any point of
procedure.

14. Real life applications of graph