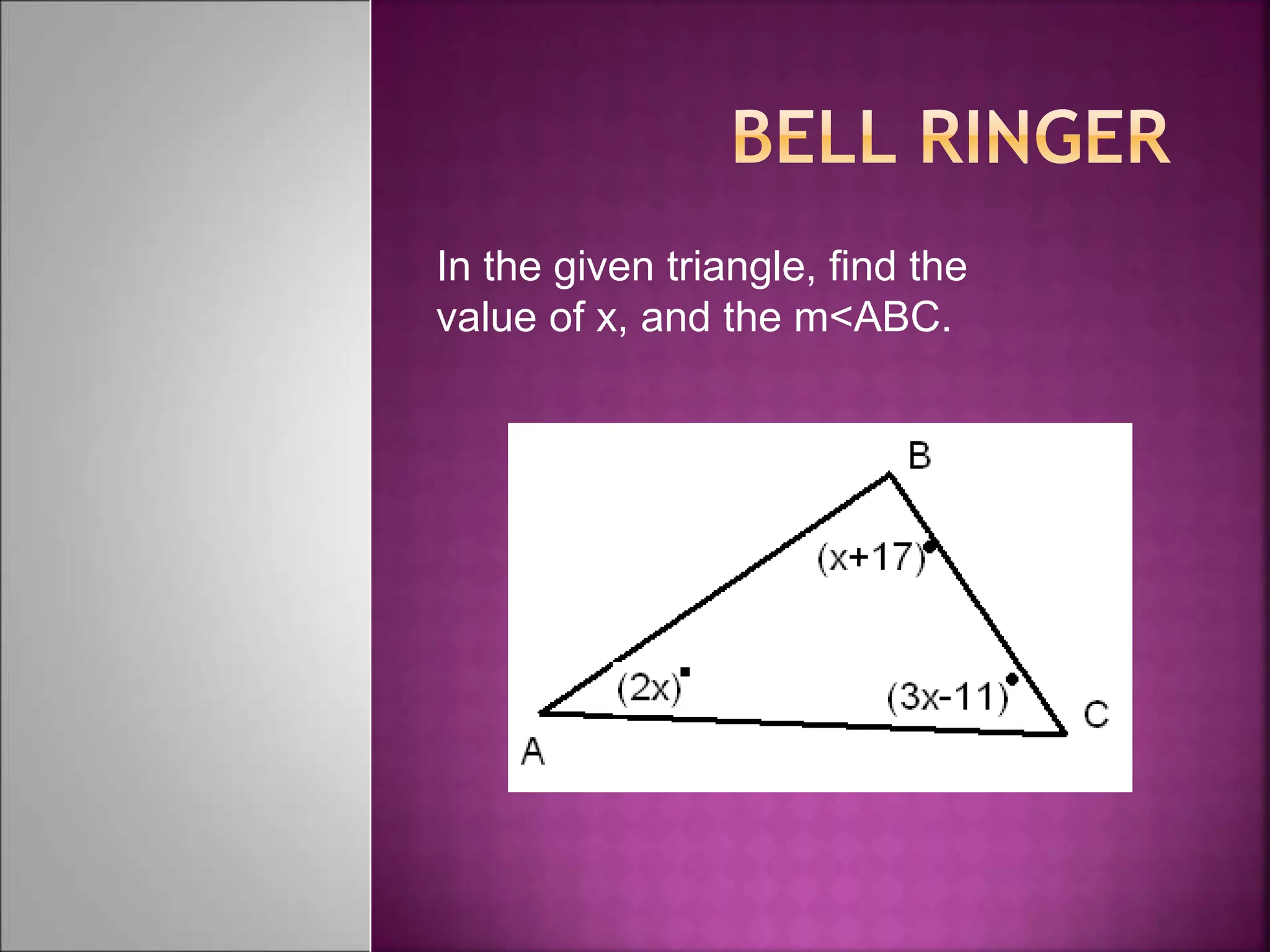
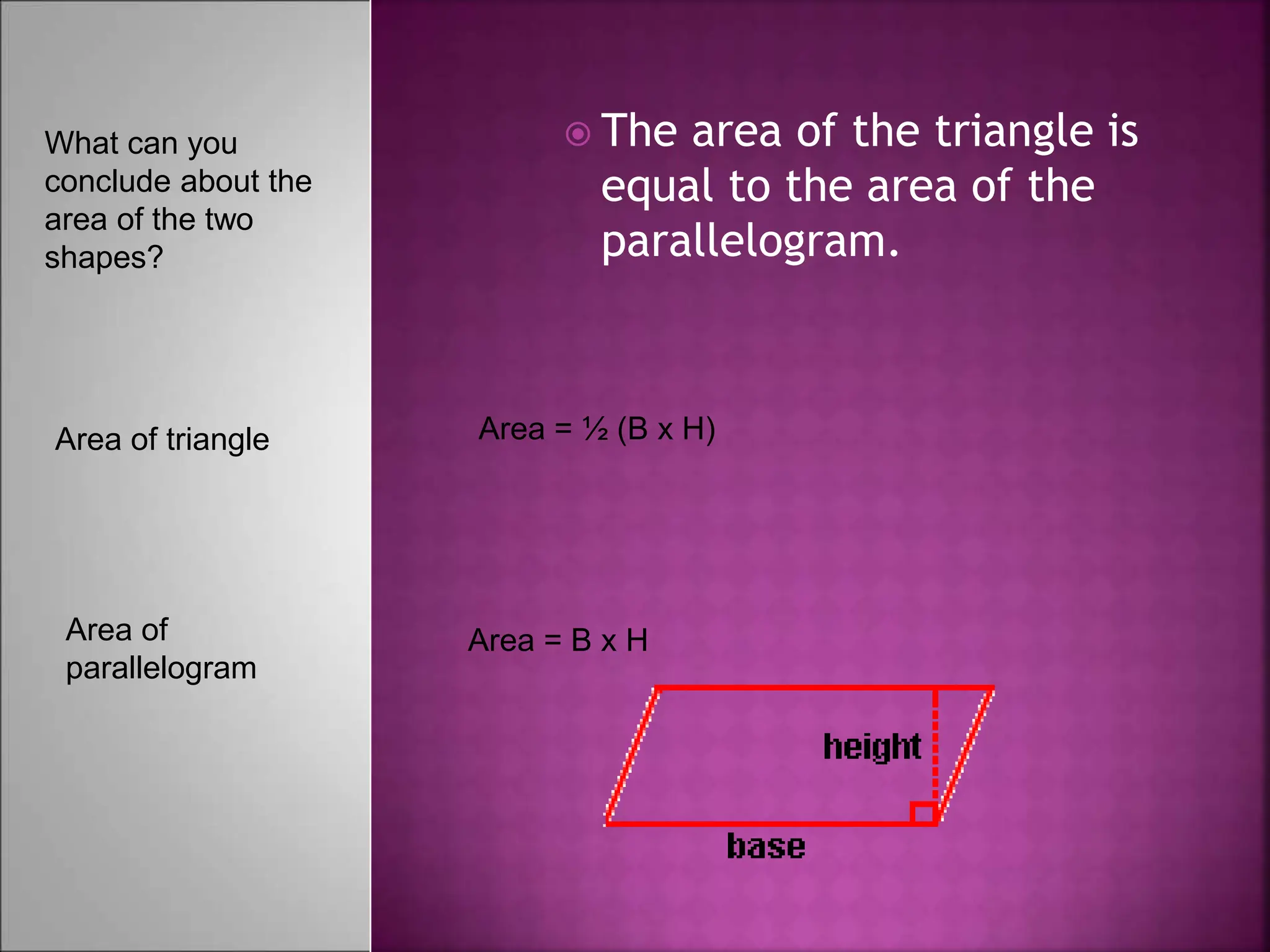
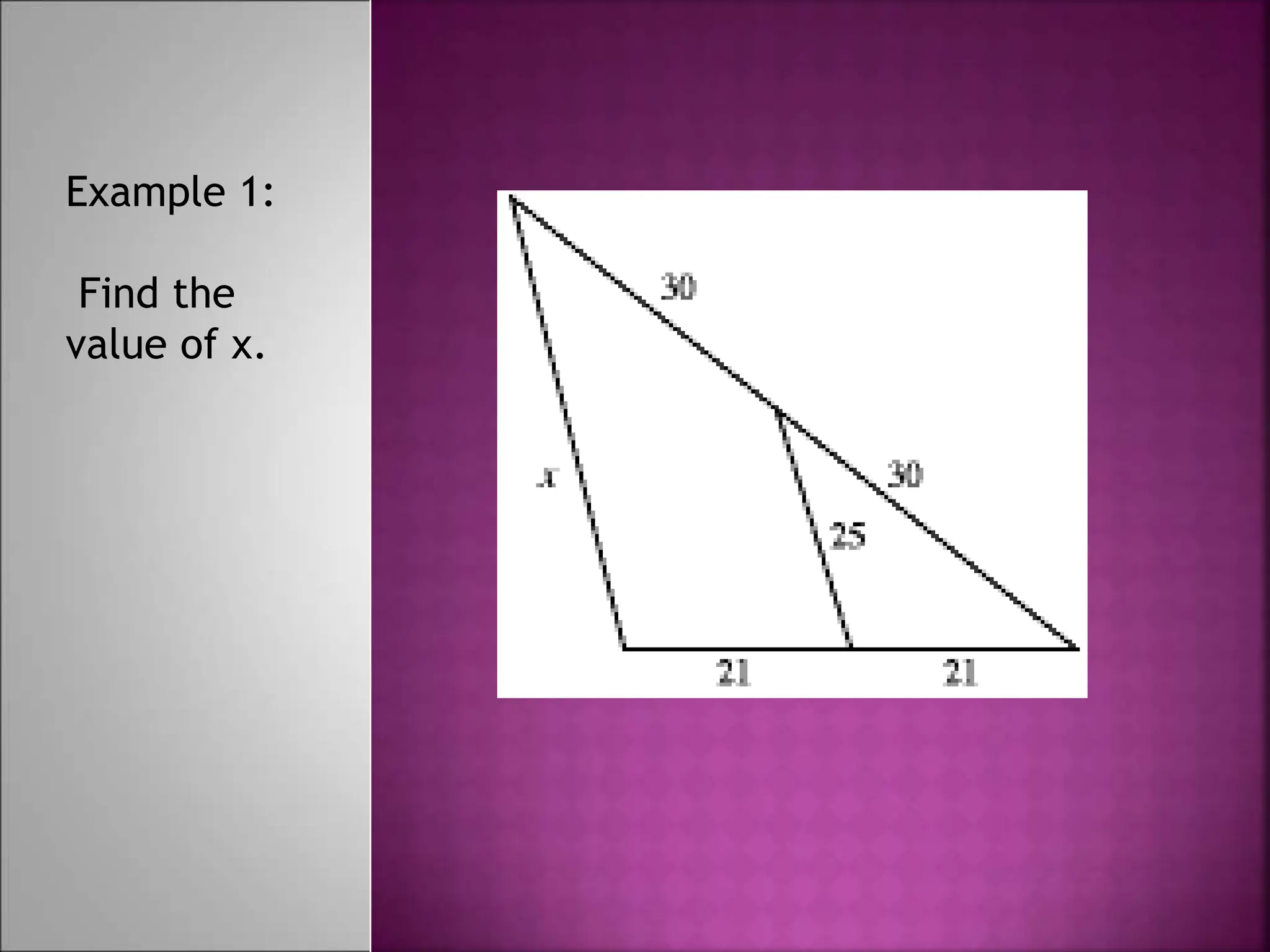
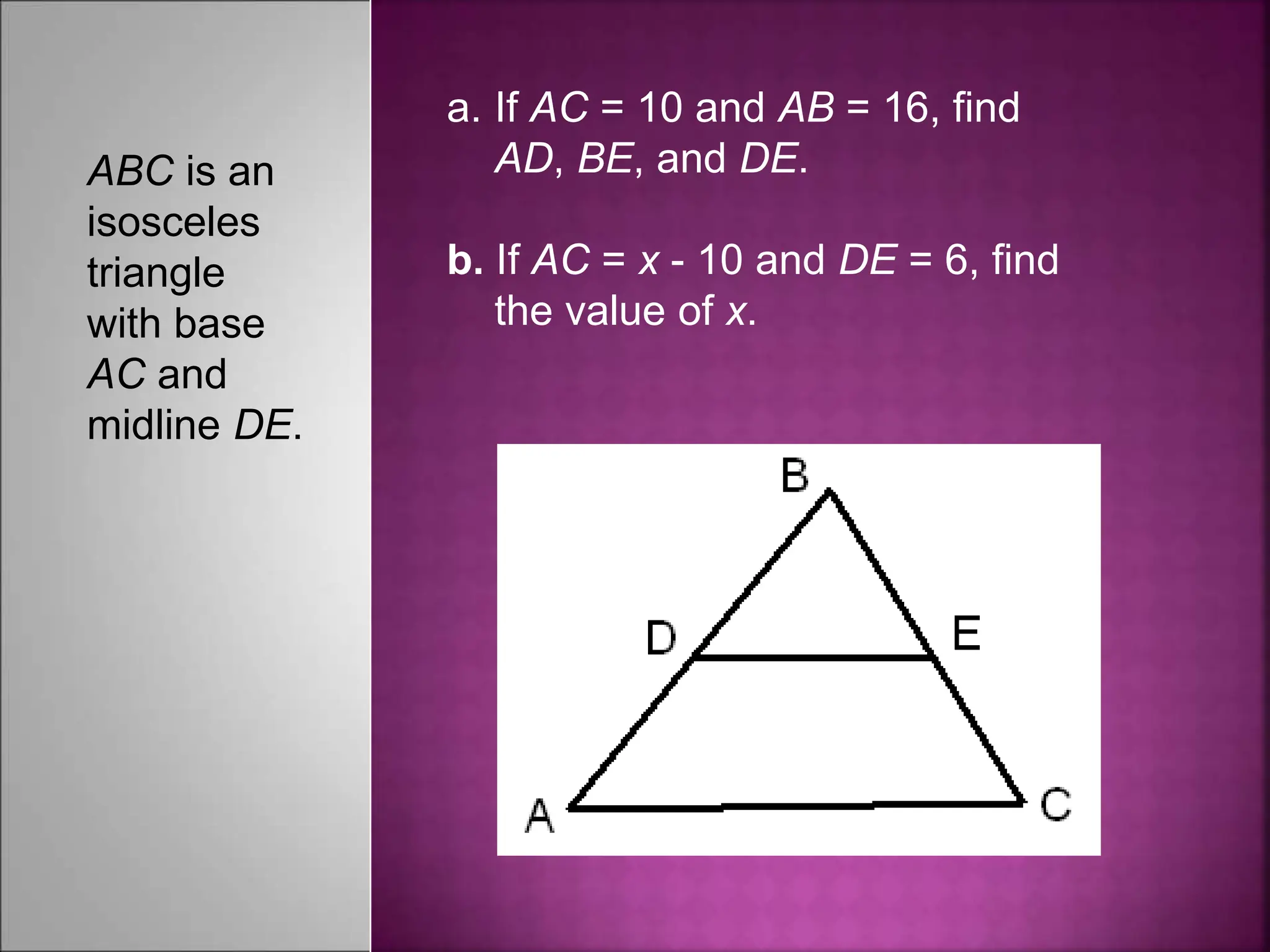
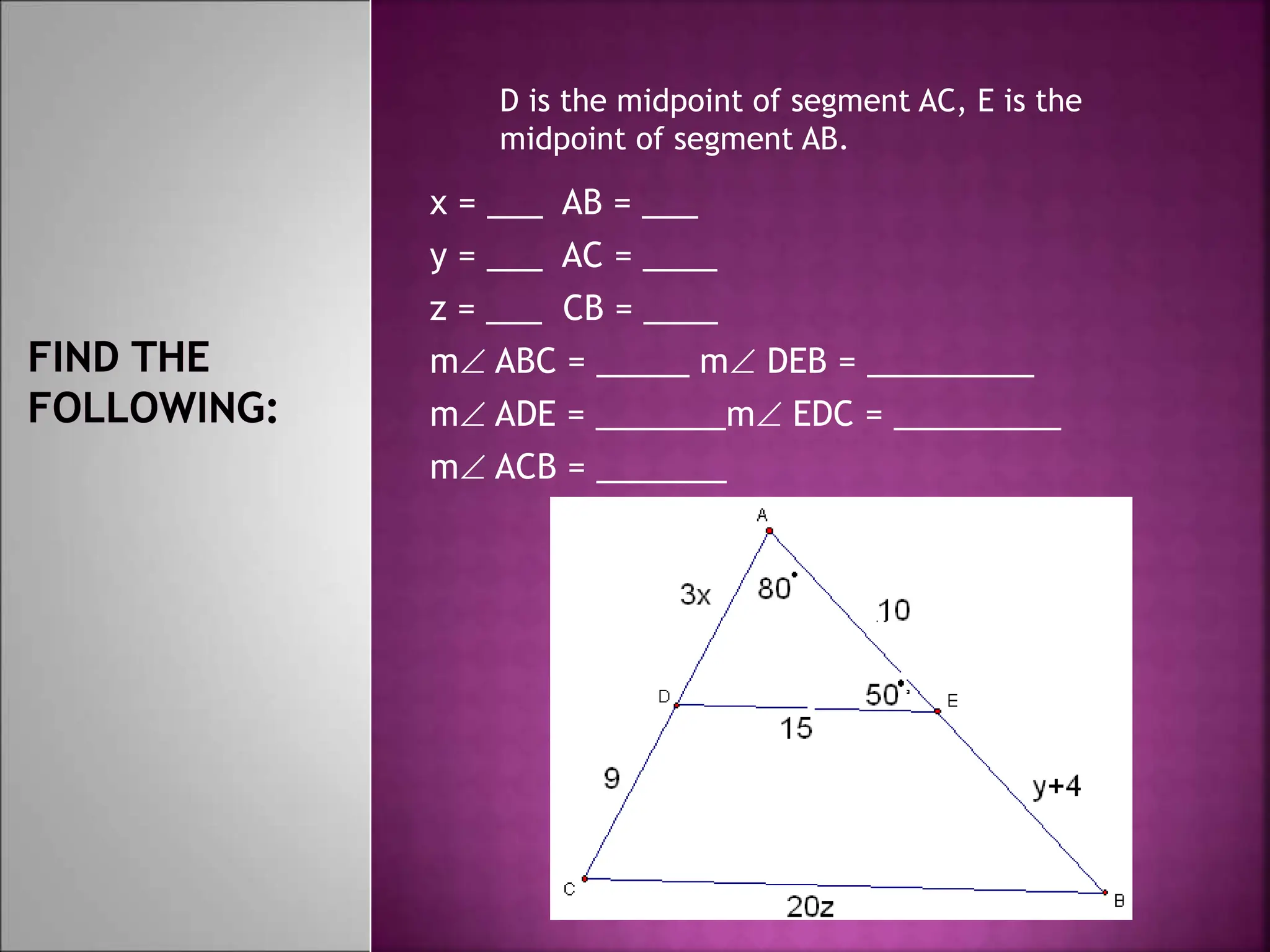
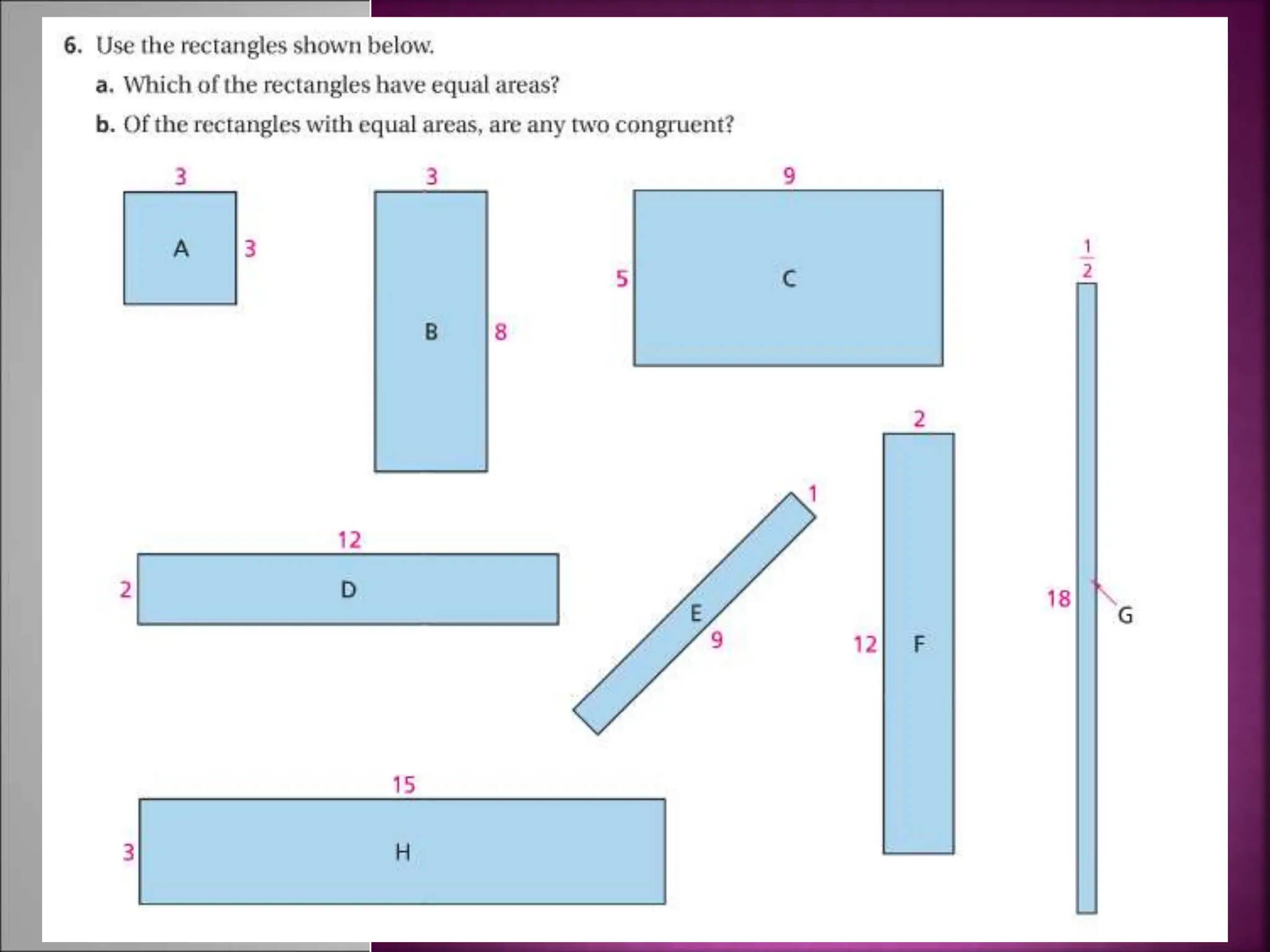
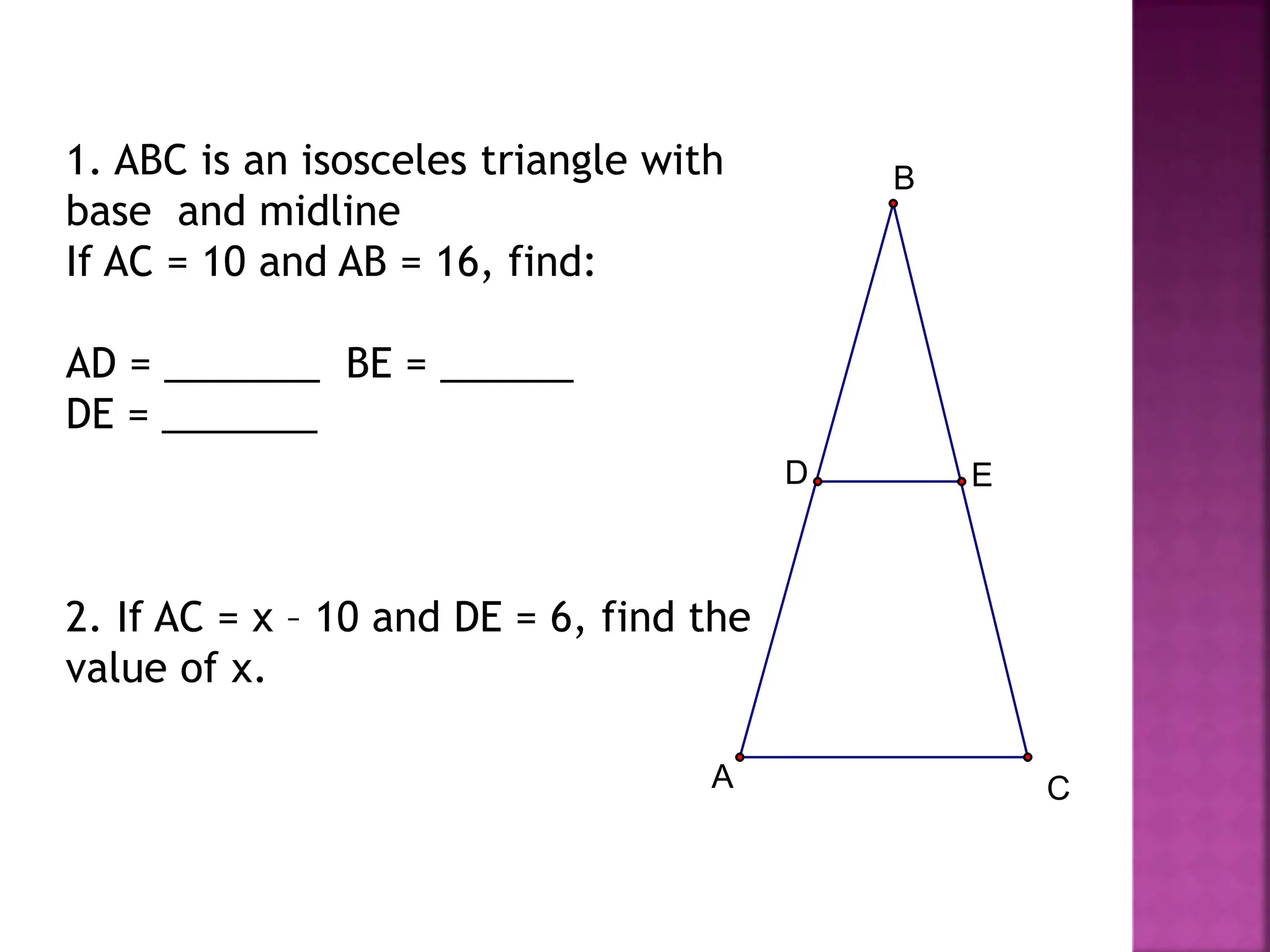
The document contains instructions for solving several geometry problems involving isosceles triangles and midlines. It asks the reader to find specific values like x, y, z, and angle measures. It also contains two example problems: the first asks you to find AD, BE, and DE given information about AC and AB in an isosceles triangle; the second provides values for AC and DE and asks you to find the value of x. The document provides diagrams of the triangles to accompany each problem or example.

1. In the given triangle, find the
value of x, and the m<ABC.

2. In the figure shown below, segment BD bisects
segment AC, and segment AB is congruent to
segment BC.
 Prove that triangle ADB and triangle CDB
are right triangles. Use a two-column
proof.

5.  The area of the triangle is
equal to the area of the
parallelogram.
What can you
conclude about the
area of the two
shapes?
Area of triangle Area = ½ (B x H)
Area of
parallelogram
Area = B x H

6. The segment joining the midpoints of two
sides of a triangle is parallel to the third
side and is half as long as the third side.
Midline
Theorem

7. Example 1:
Find the
value of x.

8. B is the midpoint of segment AC, D is the
midpoint of segment CE, and AE = 17.
Find BD.
Example 2:

9. a. If AC = 10 and AB = 16, find
AD, BE, and DE.
b. If AC = x - 10 and DE = 6, find
the value of x.
ABC is an
isosceles
triangle
with base
AC and
midline DE.

10. Find the
value of x,
y, and z.

11. x = ___ AB = ___
y = ___ AC = ____
z = ___ CB = ____
m ABC = _____ m DEB = _________
m ADE = _______m EDC = _________
m ACB = _______
D is the midpoint of segment AC, E is the
midpoint of segment AB.

12. Write Summary
 At least 3 sentences

14. 1. ABC is an isosceles triangle with
base and midline
If AC = 10 and AB = 16, find:
AD = _______ BE = ______
DE = _______
2. If AC = x – 10 and DE = 6, find the
value of x.
E
D
A
B
C