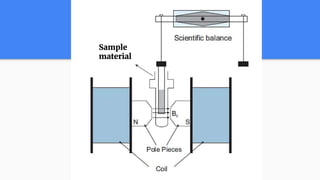
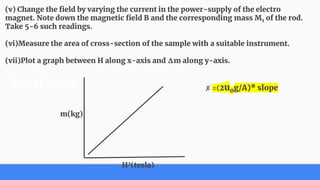
This document describes Gouy's method for determining the magnetic susceptibility of a solid sample. The method involves measuring the apparent change in weight of a long cylindrical sample placed in a non-uniform magnetic field generated by an electromagnet. The difference in weight is measured with and without the magnetic field applied. This difference is then used to calculate the magnetic susceptibility of the sample based on equations relating the force applied by the magnetic field to the susceptibility. Samples are classified based on their calculated susceptibility values as diamagnetic, paramagnetic or ferromagnetic. Potential sources of error are also discussed.

1. Solid state physics- Gouy
method Practical ppt
By Pratishtha

2. Aim-To determine the magnetic susceptibility of a
solid(Gouy’s method).
Apparatus- An electromagnet with power supply , a sensitive
balance , solid object in shape of a long cylinder ,gauss-meter
and fractional weights
Theory-(Gouy’s method):-This method depends on the force
exerted on a body placed in a non homogenous magnetic field is
obtained by measuring the apparent gain or loss in sample weight.The
variable magnetic field is provided by an electromagnet with wedge shaped pole
pieces.The field of the magnet varies rapidly along the vertical direction, due to the
wedging of the pole pieces.Thus, the force on the specimen is vertical. In this
experiment the influence of the earth's field is neglected.

3. Sample
material

4. There is a hole in the box through which the specimen hangs out. It is hung in
the field between the pole pieces of the magnet in such a way that its lower end
is in a homogeneous magnetic field H and the upper end is in a much weaker
field.
Let in absence of the magnetic field weight of sample= m0
Let in the presence of magnetic field the weight of sample= m1
Force on acting sample F=Δmg= (m1-m0)g ------(1)
We now derive an expression for the force applied by the magnet on the sample. A
substance’s magnetic permeability is given by:
u= u0(1+✘) ✘= magnetic
susceptibility.
u0= 4𝞹*10-7 Wb/A.m
We may find the difference in magnetic potential energy per unit volume between
a substance of magnetic permeability u0 and the displaced medium (in our case,
air, which has the permeability of free space):

5. Δ(U/V)= (H2/2u0) Air-(H2/2u)sample= H2/2u0-(H2/2u0(1+✘))
= ✘H2/2u0(1+✘) { ✘=M/H}
the magnetic susceptibility is significantly smaller than 1, ✘<<1
So (1+✘)≅ 1
Δ(U/V)=✘H2/2u0
Let us now consider a gradient in the field along the z-direction (upwards direction), as
there is in the case of this experiment. If we assume that the magnetic susceptibility is
constant throughout the sample, the force per unit volume f experienced by the sample
is given by:
f = -∂U/∂Z = - - - - A

6. Using Eq. A, we can then integrate over the length (with a constant cross-
sectional area A) to find the total force on the sample by the magnetic field. Here,
we will simply denote the top and the bottom z-values of the sample as “top”
and “bottom”
where A is the cross-sectional area of the sample and H is a measure of magnetic
field at the top and bottom of the sample, respectively
Htop and Hbottom are the measured magnetic fields at the top and bottom of the
sample. If the length of the sample is sufficiently long, Htop may be treated as
zero and Hbottom may be generalized to simply H. Thus, Eq. A can be simplified.
------(B)

7. From equation (1) F=Δmg
From equation (1) and (B)
✘=2u0Δmg/AH
Procedure-
(i) connect the electromagnet with power supply.
(ii) The specimen the shape of a rod is connected to one arm of a sensitive
balance and hung vertically such that its lower end is in between the two pole
pieces and the upper end outside the pole pieces.
(iii)Put the weight in the other arm of the balance so as to bring its needle in
the centre. In case of a digital weighing machine a knob is provided for the
purpose and the mass is directly given by the machine. Note down the mass
M0of the rod.
(iv) Switch on the field H and add weights in the pan to bring the balance
needle at the centre. Note down the mass M1 of the rod in the presence of the
magnetic field. Then (M1-M0) gives the mass required to counter balance the
effect of the magnetic field. Measure the field using a gauss-meter.

8. Final point
(v) Change the field by varying the current in the power-supply of the electro
magnet. Note down the magnetic field B and the corresponding mass M1 of the rod.
Take 5-6 such readings.
(vi)Measure the area of cross-section of the sample with a suitable instrument.
(vii)Plot a graph between H along x-axis and Δm along y-axis.
✘ =(2u0g/A)* slope
m(kg)
H2(tesla)

10. All material can be classified by value of magnetic susceptibility into 3
groups-
Diamagnetic -1< ✘ < 0 (repelled by magnetic f)
Paramagnetic 0< ✘ << 1 (weakly attracted)
Ferromagnetic ✘>> 1 (strongly attracted)
Precautions and source of error-- (i)The pole pieces of the electromagnetic should
be wedge shaped with enough spacing so that the field may be uniform.
(ii)The current in the electromagnet should not be passed for long time.
(iii) The balance should be very sensitive preferably a digital balance and should be
enclosed in a box so that the weighing is not affected by the air.
iv). The specimen should be freely suspended with no mechanical restraint
from the balance.

11. Weak points-Gouy's method is a simple but not a sufficiently accurate one.
This is because the force is weak even in strong fields because of the low
values of susceptibilities of dia and paramagnetic substances. To produce a
force equivalent to 1 gwt, the field required will be of the order of 10 gauss.
Other methods i) faraday’s method
ii) induction method
iii) Quink’s tube method