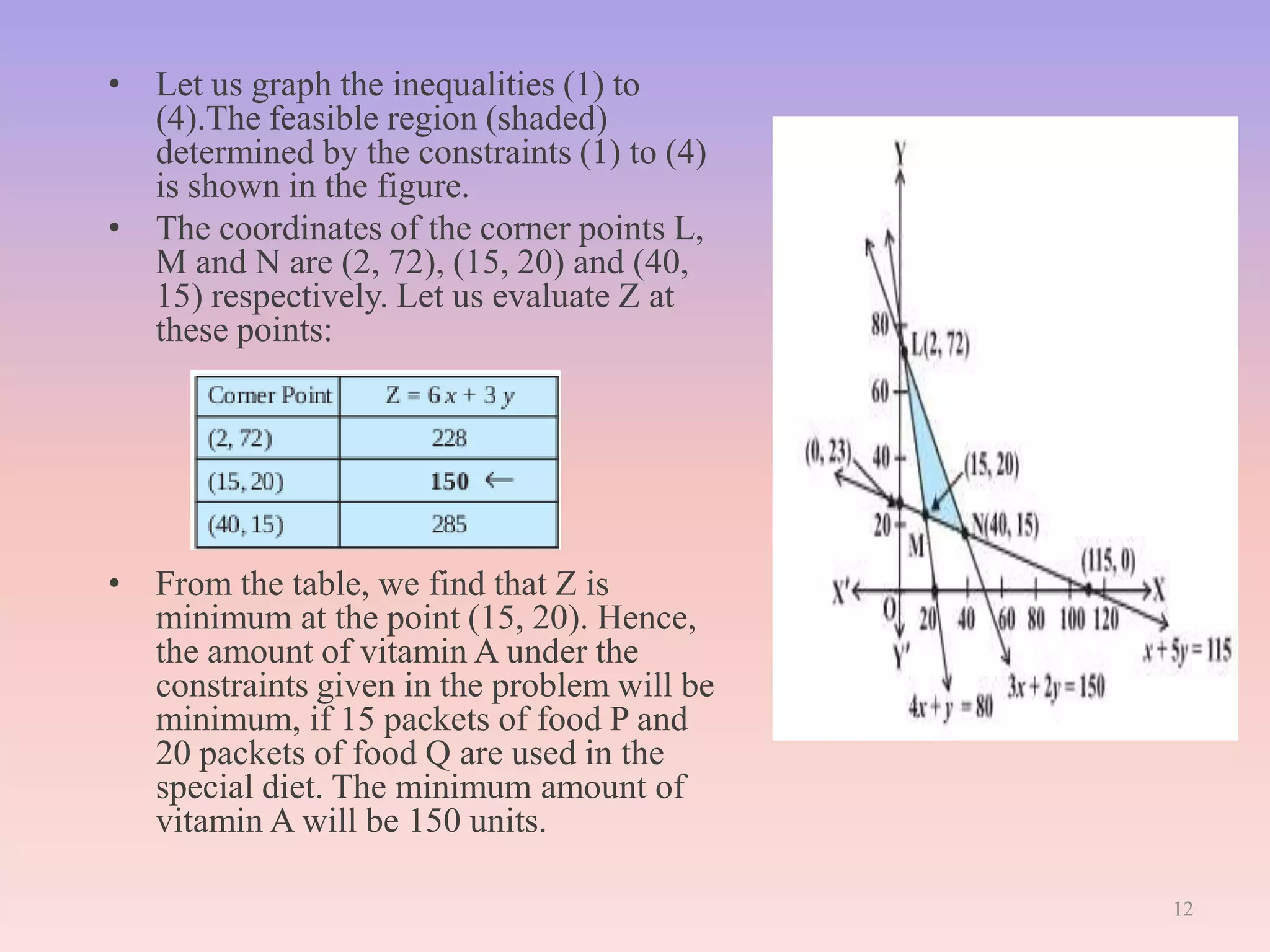
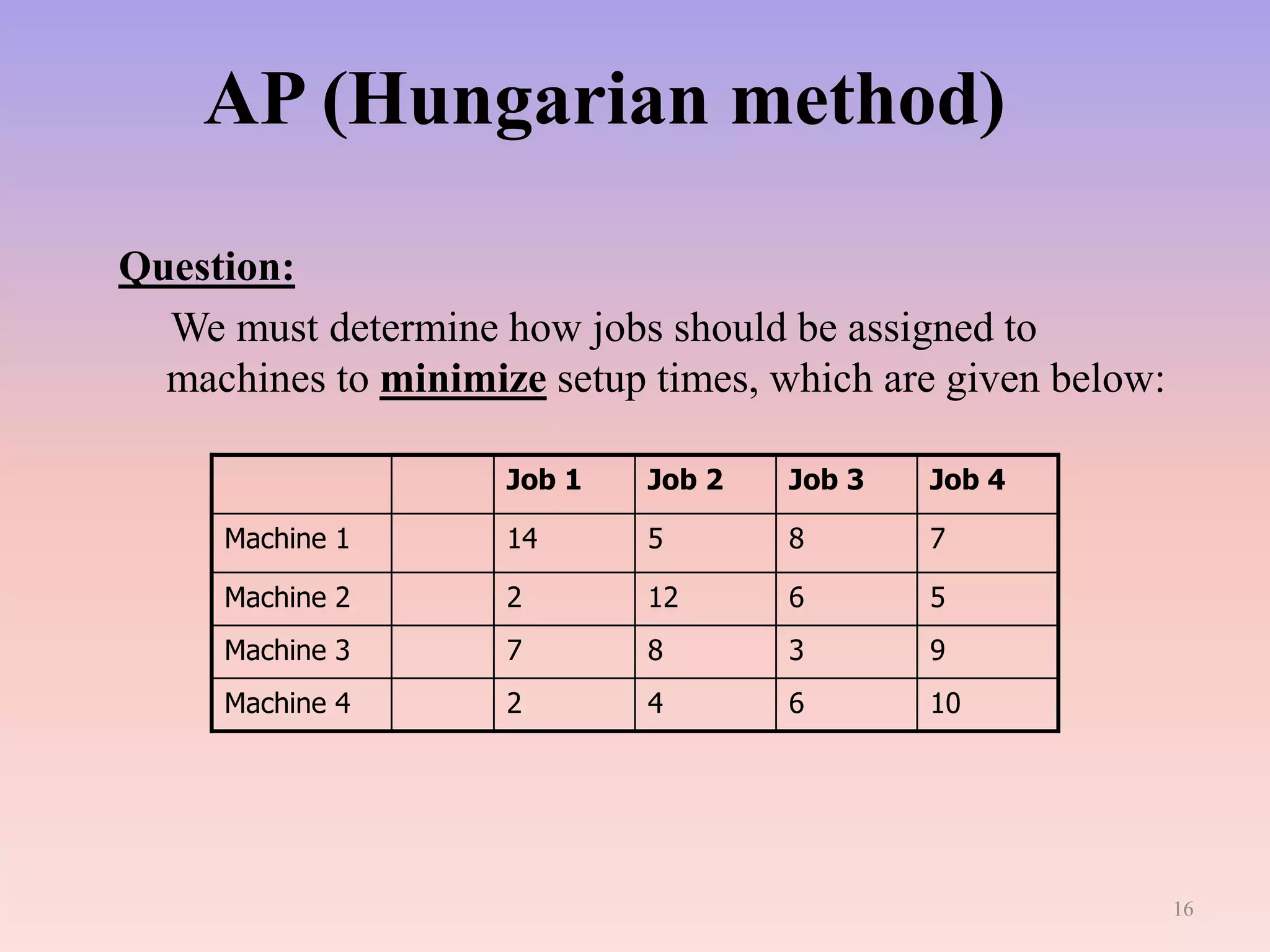
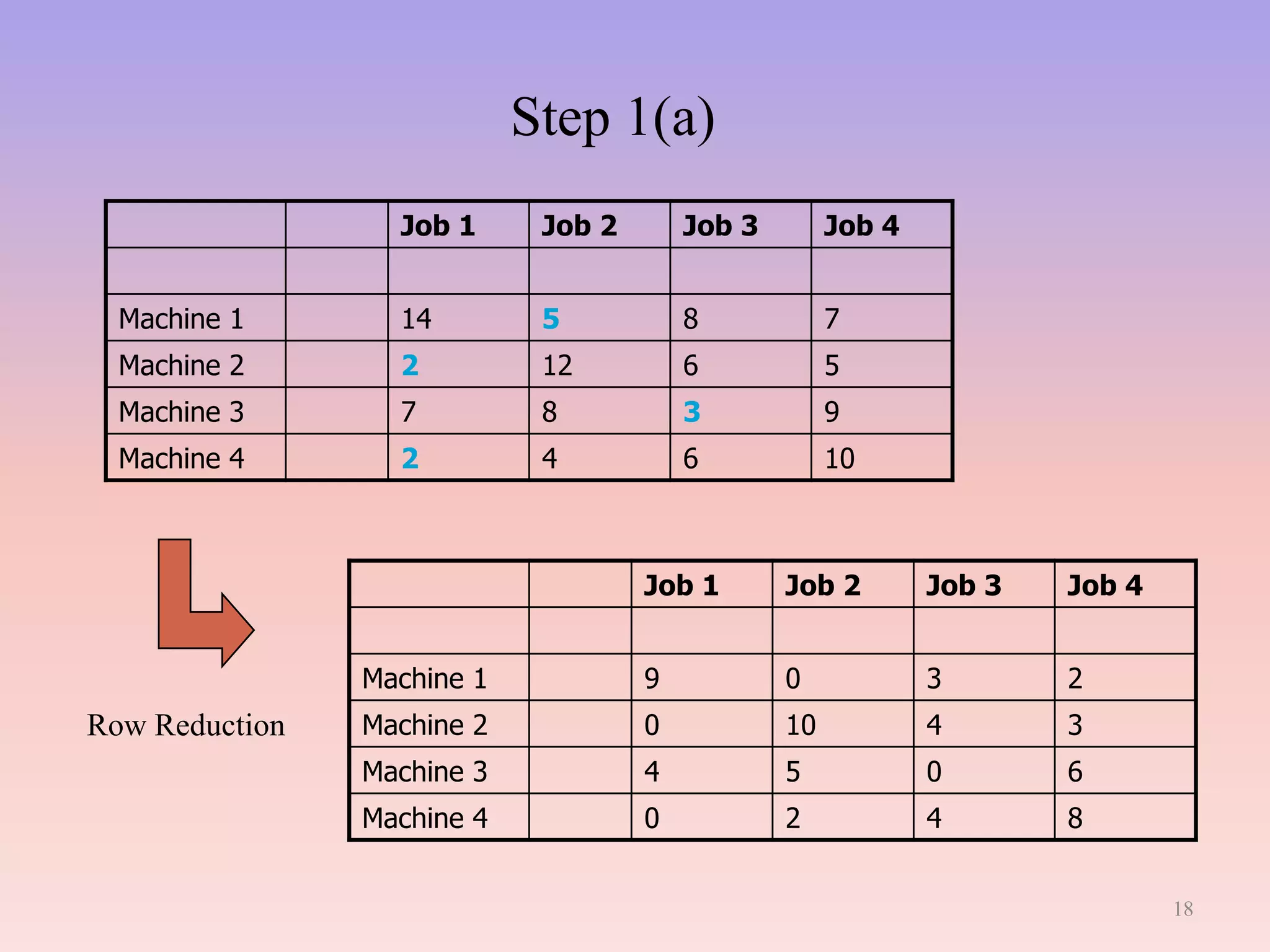
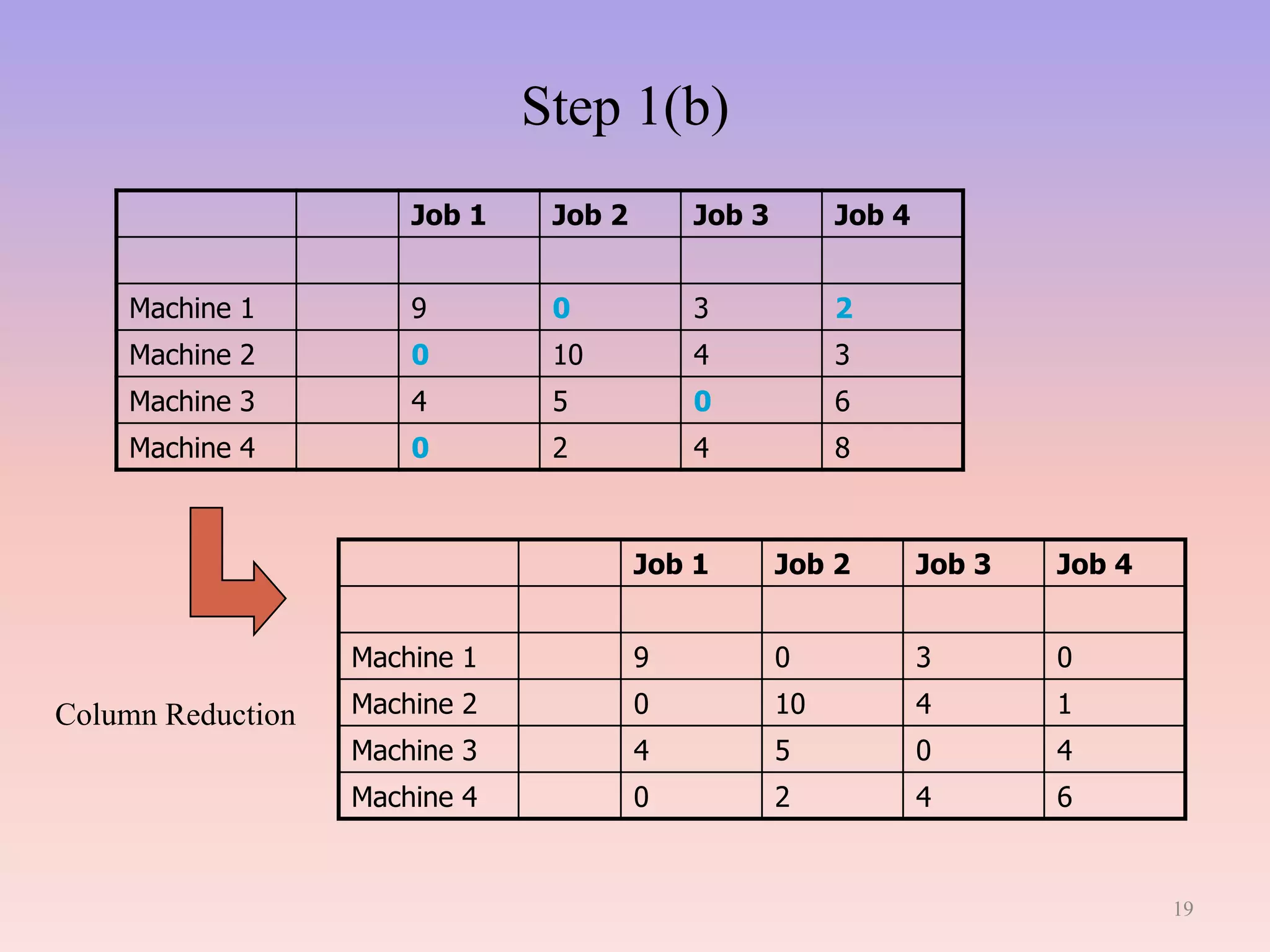
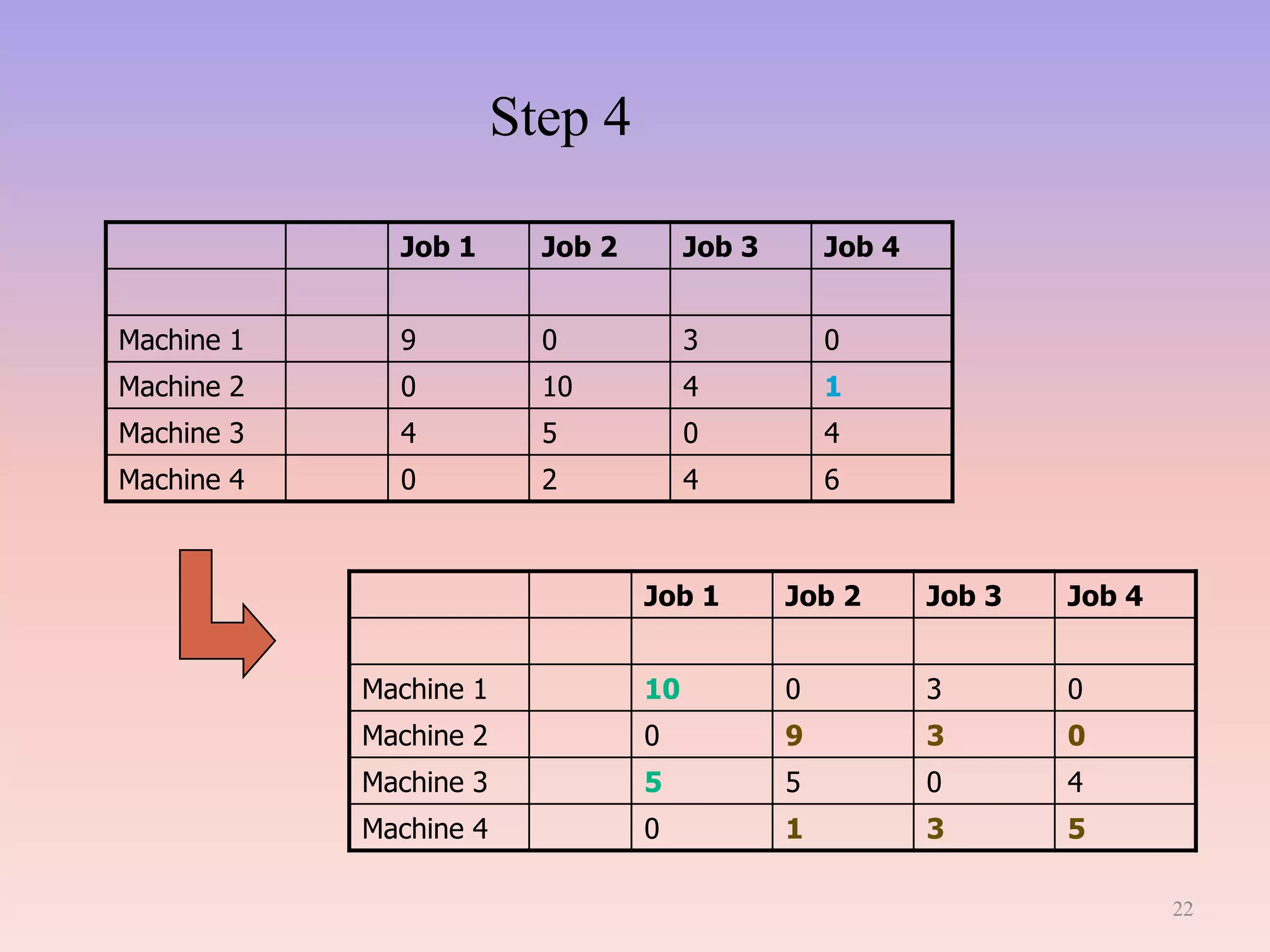
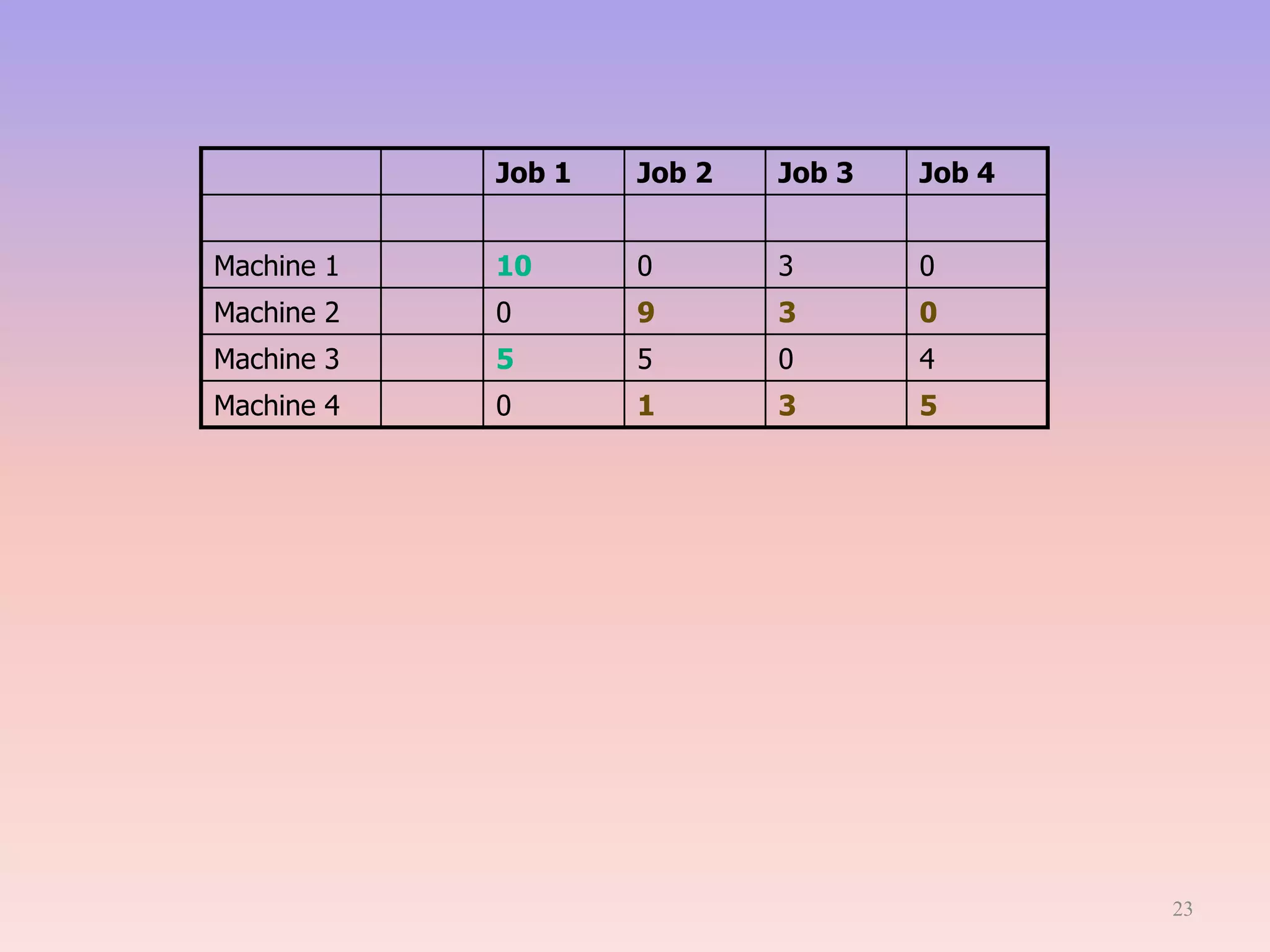
This document provides an overview of linear programming (LP). It begins with a brief introduction defining LP as a technique for determining optimal resource allocation to achieve objectives. The history of LP is then summarized, noting its development in 1947 to solve military planning problems. Key aspects of LP are outlined, including decision variables, constraints, and the objective function. Common applications are listed such as manufacturing, finance, and agriculture. An example diet problem is illustrated to demonstrate solving an LP formulation. The assignment problem as a type of LP is also described. The assumptions, methods, and limitations of LP are discussed. Finally, duality in LP is defined as analyzing a problem and its equivalent dual problem from different perspectives.

1. Presented To:
Dr. Col (Retd) Manjushree Kumar
Presented by:
Dr. Aadil
Krantee
Mrudul
Ratish

2. Contents
•
•
•
•
•
•
•
•
•
Introduction
History
Linear programming model formulation
Applications
Illustration (Diet problem)
Assignment problem
Assumptions of LP
Limitations of LP
Duality
2

3. Introduction
• Linear Programming is a mathematical modeling
technique used to determine a level of operational
activity in order to achieve an objective.
• Mathematical programming is used to find the best or
optimal solution to a problem that requires a decision or
set of decisions about how best to use a set of limited
resources to achieve a state goal of objectives.
3

4. History of linear programming
• It started in 1947 when G. B. Dantzig designed the
“simplex method” for solving linear programming
formulations of U.S. Air Force planning problems.
• It soon became clear that a surprisingly wide range of
apparently
unrelated
problems
in
production
management could be stated in linear programming
terms and solved by the simplex method.
4

5. LP Model Formulation
• Decision variables
– mathematical symbols representing levels of activity of an operation
• Objective function
– a linear relationship reflecting the objective of an operation
– most frequent objective of business firms is to maximize profit
– most frequent objective of individual operational units (such as a
production or packaging department) is to minimize cost
• Constraint
– a linear relationship representing a restriction on decision making
5

6. • Steps involved in mathematical programming
– Conversion of stated problem into a mathematical model that
abstracts all the essential elements of the problem.
– Exploration of different solutions of the problem.
– Find out the most suitable or optimum solution.
• Linear programming requires that all the mathematical
functions in the model be linear functions.
6

7. Applications
The Importance of Linear Programming
•
•
•
•
•
•
•
Hospital management
Diet management
Manufacturing
Finance (investment)
Advertising
Agriculture
Military
7

8. Some applications in Hospital management :
1) Incinerators and Pollution Control. (What is the most
economical way to make the necessary cutbacks? i.e. sulfur
dioxide emissions must be limited to 400,000 units per day
and particulate emissions to 50,000 units per day .)
2) Assignments to Hospitals .(draw up a disaster plan for
assigning casualties to hospitals in the event of a disaster.
How should the victims be assigned to minimize the total
time lost in transporting them?)
3) The Diet Problem. (e.g.. The problem is to supply the
required nutrients at minimum cost.)
4) The Transportation Problem (e.g..The problem is to meet the
hospital or patient requirements at minimum transportation
cost.)
8

9. 5) The Activity Analysis Problem. ( e.g.. The problem is to
choose the intensities which the various activities are to be
operated to maximize the value of the output to the company
subject to the given resources.)
6) The Optimal Assignment Problem. ( e.g.. The problem is to
choose an assignment of persons to jobs to maximize the total
value.)
7) The Product Mix Problem (The company would like to
determine how many units of each product it should produce
so as to maximize overall profit given its limited resources.)
8) Design of radiation therapy. (e.g.. Radiation therapy beams
affects tissues. The goal of the design is to select the
combination of beams to be used and the intensity of each
one.)
9

10. Illustration 1. Diet problem
Question:





A dietician has to develop a special diet using two foods P
and Q.
Each packet (containing 30 g) of food P contains 12 units of
calcium, 4 units of iron, 6 units of cholesterol and 6 units of
vitamin A.
Each packet of the same quantity of food Q contains 3 units
of calcium, 20 units of iron, 4 units of cholesterol and 3 units
of vitamin A.
The diet requires at least 240 units of calcium, at least 460
units of iron and at most 300 units of cholesterol.
How many packets of each food should be used to minimize
the amount of vitamin A in the diet? What is the minimum
amount of vitamin A?
10

11. Solution:
Let x and y be the number of packets of food P and Q respectively.
Obviously x ≥ 0, y ≥ 0. Mathematical formulation of the given problem
is as follows:
Minimize Z = 6x + 3y (vitamin A) subject to the constraints
12x + 3y ≥ 240 (constraint on calcium), i.e. 4x + y ≥ 80
... (1)
4x + 20y ≥ 460 (constraint on iron.), i.e. x + 5y ≥ 115
... (2)
6x + 4y ≤ 300 (constraint on cholestérol), i.e. 3x + 2y ≤ 150
... (3)
x ≥ 0, y ≥ 0
... (4)
11

12. • Let us graph the inequalities (1) to
(4).The feasible region (shaded)
determined by the constraints (1) to (4)
is shown in the figure.
• The coordinates of the corner points L,
M and N are (2, 72), (15, 20) and (40,
15) respectively. Let us evaluate Z at
these points:
• From the table, we find that Z is
minimum at the point (15, 20). Hence,
the amount of vitamin A under the
constraints given in the problem will be
minimum, if 15 packets of food P and
20 packets of food Q are used in the
special diet. The minimum amount of
vitamin A will be 150 units.
12

13. Assignment problem
• The assignment problem refers to the class of
linear programming problems that involve
determining the most efficient assignment of
assignees to perform tasks.
 people to projects
 salespeople to territories
 contracts to bidders
 jobs to machines, etc.
• The objective is most often to minimize total
costs or total time of performing the tasks at hand.
13

14. • To fit the definition of an assignment problem, these
kinds of applications need to be formulated in a way
that satisfies the following assumptions.
1.The number of assignees and the number of tasks are
the same. (This number is denoted by n.)
2.Each assignee is to be assigned to exactly one task.
3.Each task is to be performed by exactly one assignee.
4.There is a cost cij associated with assignee i (i1, 2,...,n)
performing task j (j1, 2, . . . ,n).
5.The objective is to determine how all assignments
should be made to minimize the total cost.
14

15. Assignment problem solving
methods
1.
2.
3.
4.
Hungarian Method
Enumeration method
Simplex method
Transportation
15

16. AP (Hungarian method)
Question:
We must determine how jobs should be assigned to
machines to minimize setup times, which are given below:
Job 1
Job 2
Job 3
Job 4
Machine 1
14
5
8
7
Machine 2
2
12
6
5
Machine 3
7
8
3
9
Machine 4
2
4
6
10
16

17. • Step 1: (a) Find the minimum element in
each row of the cost matrix. Form a new
matrix by subtracting this cost from each
row. (b) Find the minimum cost in each
column of the new matrix, and subtract this
from each column. This is the reduced cost
matrix.
17

18. Step 1(a)
Job 1
Job 2
Job 3
Job 4
Machine 1
14
5
8
7
Machine 2
2
12
6
5
Machine 3
7
8
3
9
Machine 4
2
4
6
10
Job 1
Job 3
Job 4
Machine 1
Row Reduction
Job 2
9
0
3
2
Machine 2
0
10
4
3
Machine 3
4
5
0
6
Machine 4
0
2
4
8
18

19. Step 1(b)
Job 1
Job 2
Job 3
Job 4
Machine 1
9
0
3
2
Machine 2
0
10
4
3
Machine 3
4
5
0
6
Machine 4
0
2
4
8
Job 1
Job 2
Job 3
Job 4
Machine 1
9
0
3
0
Machine 2
0
10
4
1
Machine 3
4
5
0
4
Machine 4
0
2
4
6
Column Reduction
19

20. Step 2
Draw the minimum number of lines that are needed to
cover all the zeros in the reduced cost matrix. If m lines are
required, then an optimal solution is available among the
covered zeros in the matrix. Otherwise, continue to Step 3.
Job 1
Job 2
Job 3
Job 4
Machine 1
9
0
3
0
Machine 2
0
10
4
1
Machine 3
4
5
0
4
Machine 4
0
2
4
6
20

21. Step 3
Find the smallest nonzero element (say, k)
in the reduced cost matrix that is uncovered
by the lines. Subtract k from each
uncovered element, and add k to each
element that is covered by two lines. Return
to Step 2.
21

22. Step 4
Job 1
Job 2
Job 3
Job 4
Machine 1
9
0
3
0
Machine 2
0
10
4
1
Machine 3
4
5
0
4
Machine 4
0
2
4
6
Job 1
Job 2
Job 3
Job 4
Machine 1
10
0
3
0
Machine 2
0
9
3
0
Machine 3
5
5
0
4
Machine 4
0
1
3
5
22

23. Job 1
Job 2
Job 3
Job 4
Machine 1
10
0
3
0
Machine 2
0
9
3
0
Machine 3
5
5
0
4
Machine 4
0
1
3
5
23

24. Assumptions of LP
1. Certainty:

numbers in the objective and constraints are known with
certainty and do not change during the period being
studied
2. Proportionality:


exists in the objective and constraints
constancy between production increases and resource
utilization
3. Additivity:

the total of all activities equals the sum of the individual
activities
24

25. Assumptions of LP cont…
4. Divisibility:


solutions need not be in whole numbers (integers)
solutions are divisible, and may take any fractional
value
5. Non-negativity:


all answers or variables are greater than or equal to (≥)
zero
negative values of physical quantities are impossible
25

26. Limitations of LP
•It treats all relationships among decision variables as linear.
•There is no guarantee that we will get integer value
solutions. e.g. 2.5 machines
•LP does not take into consideration the effect of time &
uncertainty.
•In LP parameters are assumed to be constant ; but in real life
situations majority of the times they are neither known nor
constant.
•LP deals with only single objective whereas in real life
conflicting situations may have to be solved.
26

27. Duality in LP
•In context of LP, duality means each LP problem can be
analyzed in two different ways.
•LP problem can be stated in another equivalent problem based
on the same data and new problem will be called as DUAL.
•The main focus of a dual problem is to find best marginal
value for each resource; also known as Shadow Prize.
•The shadow prize is also defined as change in optimal
objective function value with respect to unit change in
availability of resource.
27

28. 28

29. REFERENCES
•
•
•
•
•
www.math.ucla.edu/~tom/LP.pdf
www.sce.carleton.ca/faculty/chinneck/po/Chapter2.
www.markschulze.net/LinearProgramming.pdf
web.ntpu.edu.tw/~juang/ms/Ch02.
cmp.felk.cvut.cz/~hlavac/Public/.../Linear%20Progra
mming-1.ppt
• www.slideshare.net/
29

30. Questions/
Queries?
30

31. 31