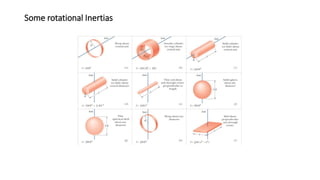
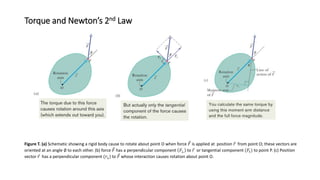
The document discusses rotational kinetic energy and rotational inertia. It defines rotational kinetic energy as 1/2Iω2, where I is the rotational inertia and ω is the angular velocity. Rotational inertia, analogous to mass in linear motion, is a measure of an object's resistance to changes in its rotational motion. It provides an example of calculating the rotational kinetic energy of a uniform disk rotating about a fixed axis, given its moment of inertia, angular acceleration, and time.

1. University of Zululand
Rotational kinetic energy, and rotational inertia
March 20, 2023

2. • Considers the kinetic energy of a rigid body rotating about an axis
• It is composed of other small bodies of mass 𝑚𝑖 and at separation
distance 𝑟𝑖 from axis of rotation and the kinetic energy of a rigid body
is expressed as:
𝐾 = 𝑖=1
𝑁 1
2
𝑚𝑖𝑣𝑖
2
= 𝑖=1
𝑁 1
2
𝑚𝑖 𝑟𝑖𝜔 2
= 𝑖=1
𝑁 1
2
𝐼𝑖𝜔2, (1)
where 𝜔 is the angular velocity for all bodies constituting a rotating
rigid body and 𝐼 = 𝑖=1
𝑁
𝑚𝑖𝑟𝑖
2
is rotational inertia/moment of inertia
which is analogous to mass in linear motion equations. Therefore 𝐼𝑖 can
be thought of as a resistant of a body to undergo rotational motion.
𝐾 = 𝑖=1
𝑁 1
2
𝐼𝑖𝜔2 = 1
2
𝐼𝜔2(radian).
Rotational Kinetic Energy

3. Some rotational Inertias

4. Torque and Newton’s 2nd Law
Figure T. (a) Schematic showing a rigid body cause to rotate about point O when force 𝐹 is applied at position 𝑟 from point O; these vectors are
oriented at an angle ∅ to each other. (b) force 𝐹 has a perpendicular component 𝐹⊥ to 𝑟 or tangential component (𝐹𝑡) to point P. (c) Position
vector 𝑟 has a perpendicular component (𝑟⊥) to 𝐹 whose interaction causes rotation about point O.

5. Torque
• When opening a door you need to apply a force F at an angle close to right-angle and far
enough (separation displacement r ) from hinges, otherwise more force would be
needed if the you pushed close to hinges or at an angle very different from 900.
• As shown for Figure T (b) – (c ) even though 𝐹 and 𝑟 were oriented at angle 𝜙 which was
different from 900
they both have perpendicular components relative to each vector
enabling easy rigid body rotation
• The interaction of 𝐹 and 𝑟 can be visualized using a vector or cross product,
𝜏 = 𝑟 × 𝐹, and this result in another vector known as torque whose direction can be
determined by right-hand rule and the magnitude is,
𝜏 = 𝑟⊥𝐹 = 𝑟𝑠𝑖𝑛𝜙 𝐹 = 𝑟𝐹𝑡 = 𝑟 𝐹𝑠𝑖𝑛𝜙 = 𝑟𝐹𝑠𝑖𝑛𝜙.
• Unit of torque 𝜏 is 𝑁. 𝑚, but do not confused it with Work which has the same SI units

6. Newton’s 2nd Law
• Having previously shown the analogy of linear and rotational motion, we can further
show that Newton’s 2nd law applies to rotational motion
𝐹𝑡 = 𝑚𝑎𝑡 = 𝑚𝛼𝑟 (1)
Multiplying both side of (1) by 𝑟 yields:
𝜏 = 𝑟𝐹𝑡 = 𝑟𝑚𝑎𝑡 = 𝑚𝑟2 𝛼 = 𝐼𝛼 (2)
Therefore Newton’s second law for rotational motion is
𝜏𝑛𝑒𝑡 = 𝐼𝛼

7. Worked Examples
1. Figure Ex1 shows a uniform disk, with mass 𝑀 = 2.5 𝑘𝑔 and radius 𝑅 = 20 𝑐𝑚, mounted on a
fixed horizontal axle. A block with mass 𝑚 = 1.2 𝑘𝑔 hangs from a massless cord that is
wrapped around the rim of the disk. Find the acceleration of the falling block, the angular
acceleration of the disk, and the tension in the cord. The cord does not slip, and there is no
friction at the axle.
Figure Ex1.

8. Worked Problems….
For the block with mass 𝑚 = 1.2 𝑘𝑔:
𝑇 − 𝑚𝑔 = 𝑚(−𝑎) (1)
For a solid disk with mass 𝑀 = 2.5 𝑘𝑔:
Since 𝜏𝑛𝑒𝑡 = 𝐼𝛼
𝐼 =
1
2
𝑀𝑅2
(moment of inertia of solid disk), and
−𝑅𝑇 =
1
2
𝑀𝑅2(−𝛼), and dividing both sides by 𝑅 and solve for 𝑇 would yield:
𝑇 =
1
2
𝑀𝛼 =
1
2
𝑀𝑎𝑡 =
1
2
𝑀𝑎 (2)
𝑎 = 4.8 𝑚/𝑠2 and T can be calculated from (2) and 𝑇 = 6.0 𝑁
𝛼 =
𝑎
𝑅
=
4.8
0.20
= 24 𝑟𝑎𝑑/𝑠2

9. Worked Problems….
2. Let the disk in Figure Ex1 start from rest at time 𝑡 = 0 and also let the tension in the
massless cord be 6.0 𝑁 and the angular acceleration of the disk be −24 𝑟𝑎𝑑/𝑠2. What is
its rotational kinetic energy 𝐾 at 𝑡 = 2.5 𝑠?
Solution:
You already calculated 𝐼 =
1
2
𝑀𝑅2
and the acceleration is a constant (−24 𝑟𝑎𝑑/𝑠2
)
and therefore equations of motion can be used.
𝐾 =
1
2
𝐼𝜔2
, while 𝜔0 = 0 𝑟𝑎𝑑/𝑠 at time 𝑡 = 0 𝑠, what is 𝜔 at time 𝑡 = 2.5 𝑠?
Using equations of motions one can work out 𝜔,
𝜔 = 𝜔0 + 𝛼𝑡,
𝜔 = 0 − 24 2.5 = −60 𝑟𝑎𝑑/𝑠, and 𝐾 =
1
2
𝐼𝜔2
=
1
2
1
2
2.5 0.20 2
−60 2
= 90 J