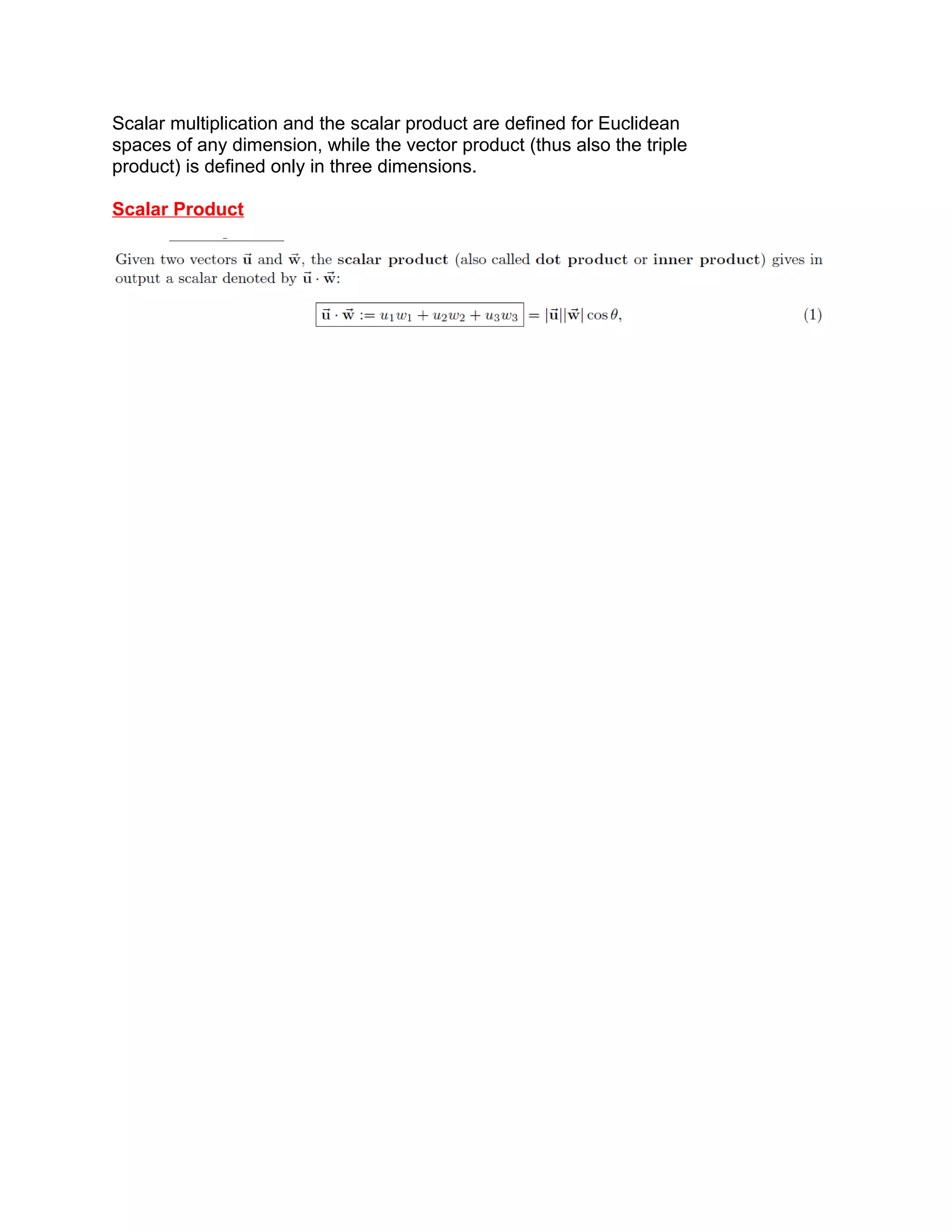
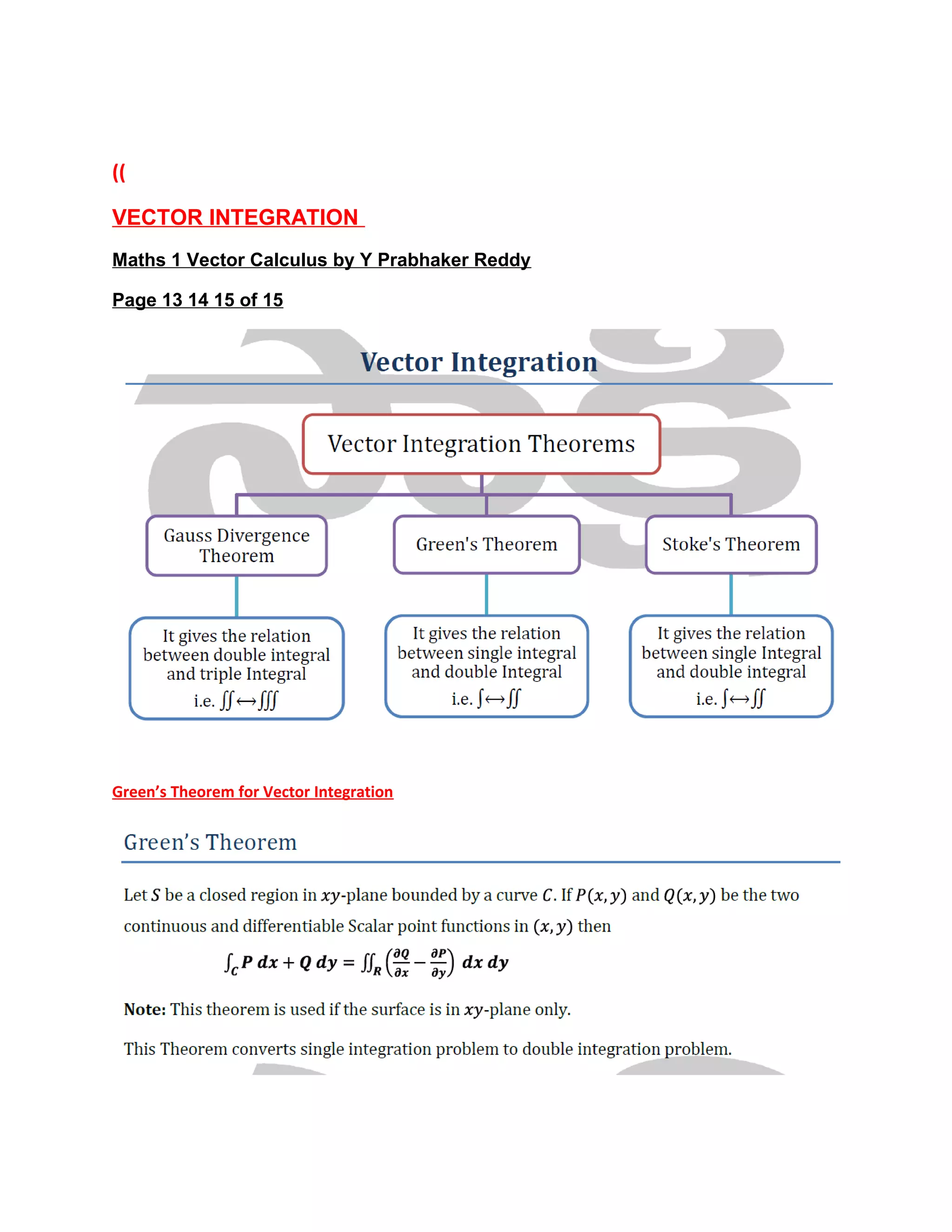
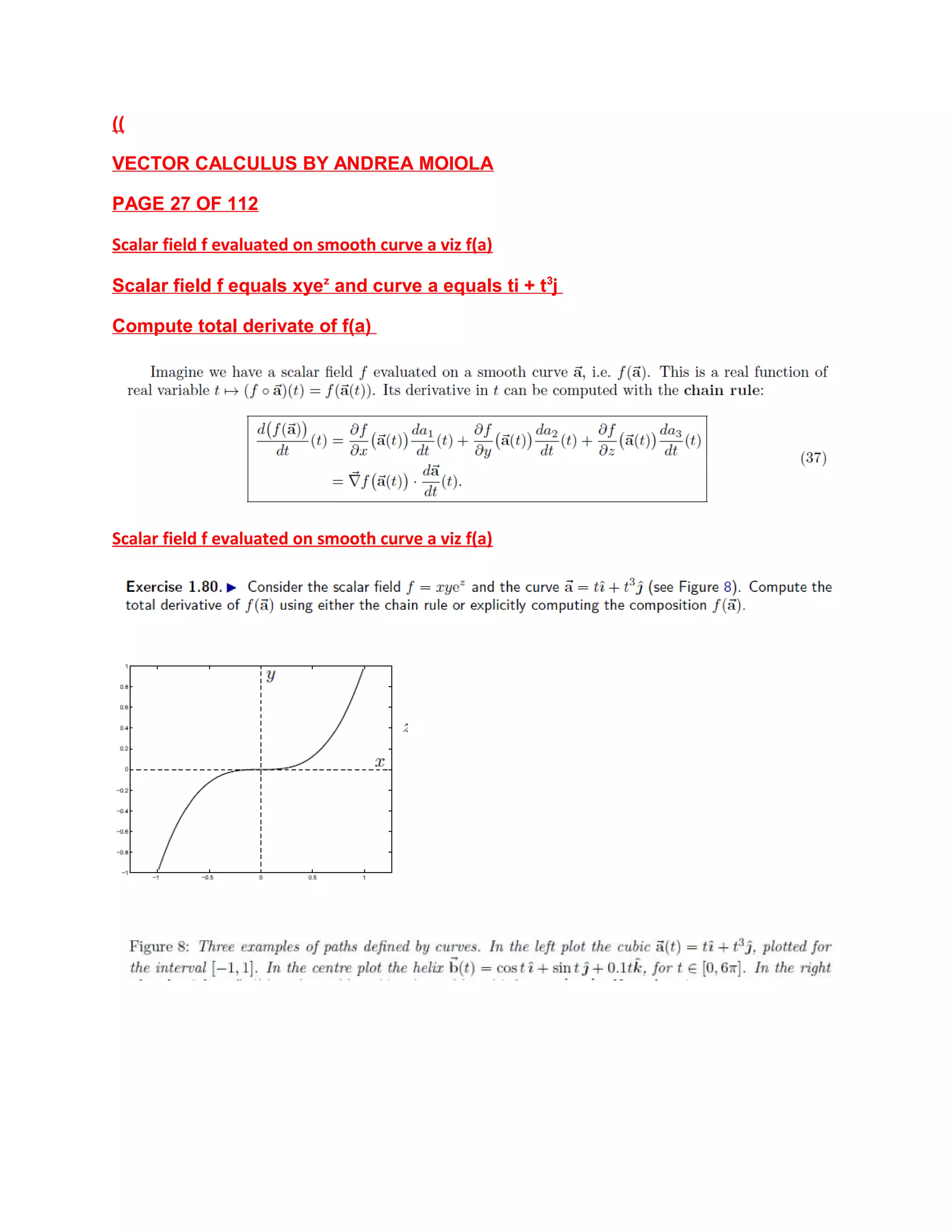
This document provides notes on vector calculus from a lecture by Professor Andrea Moiola of the University of Reading. It covers topics including position vectors, scalar and vector fields defined over subsets of Euclidean space, the gradient and directional derivative of scalar fields, and properties of the vector product. Key concepts discussed include using partial derivatives to analyze scalar and vector fields, and how the gradient and curl operators relate to directional changes in scalar and vector quantities over three-dimensional space.























![Page 7
Scalar functions in particular real functions of a real variable viz rules that
associate to every number t ∈ R a second number f(t) ∈ R.
Scalar functions in particular real functions of a real variable viz
rules that associate to every number Real Number to second Real
number
Vector functions whose domains or codomains or both are three
dimensional Euclidean space viz Real Number cubed as opposed to
real line R
Three different extensions of concept to Vector case viz consider functions
whose domains or codomains or both are three dimensional Euclidean
space as opposed to the real line R.
.
Remark 1.27 we summarise the mapping properties of all these objects.
Scalar fields, vector fields and
vector functions are described in [1] in Sections 12.1, 15.1 and 11.1
respectively.
Scalar Field is function where domain D is an open subset of
Euclidean Space
Scalar field is a function where domain d is an open subset of
Euclidean Space
Scalar field value viz Value of function at the point r may be written
as f(r) or f(x y z)
r is point
Scalar field can equivalently be interpreted as a function of one
vector variable or as a function of three scalar variables](https://image.slidesharecdn.com/notesnotesvectorcalculusmadeathomewecompress-190301174501/75/Notes-notes-vector-calculus-made-at-home-wecompress-com-25-2048.jpg)