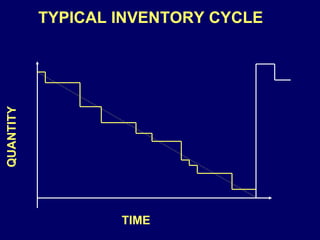
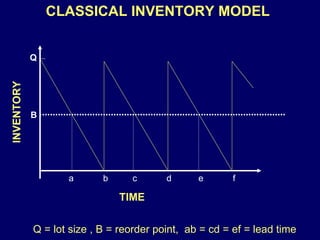
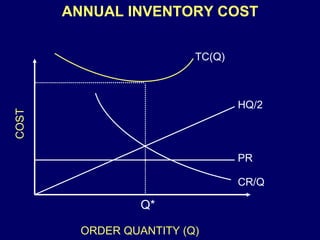
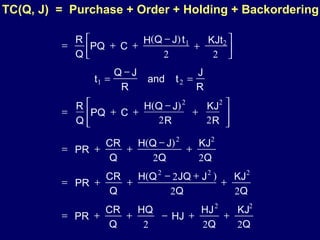
The document discusses inventory management models including the classical inventory model, economic order quantity (EOQ) model, sensitivity analysis of parameters in the EOQ model, backordering inventory model, quantity discounts, and handling known price increases. It provides formulas for determining optimal order quantities and total costs under different assumptions.

1. Stock Available Demand Occurs (units withdrawn) Determine Stock Position (on hand + on order - backorders) Is Stock Position  Reorder Point ? Issue Replenishment Order stock receipt FIXED ORDER SIZE SYSTEM no yes

2. TYPICAL INVENTORY CYCLE TIME QUANTITY

3. CLASSICAL INVENTORY MODEL a b c d e f TIME Q = lot size , B = reorder point, ab = cd = ef = lead time INVENTORY B Q

4. TOTAL ANNUAL COST = PURCHASE + ORDER + HOLDING 2 HQ Q CR PR (Q) = TC + + 0 2 H Q CR dQ ) Q ( dTC 2 = + - = PF CR 2 H CR 2 * Q = = = EOQ

5. ANNUAL INVENTORY COST ORDER QUANTITY (Q) Q* COST TC(Q) HQ/2 PR CR/Q

6. 2 HQ Q CR PR ) Q ( TC    OPTIMUM TOTAL ANNUAL COST 2 * HQ 2 * HQ PR    2 * HQ H / CR 2 * CRQ PR    2 * HQ * Q * Q * CRQ PR    2 * HQ * Q CR PR *) Q ( TC    If Q = Q*, then : * HQ PR   *) Q ( TC

7. INVENTORY STOCK POSITION (B > Q) QUANTITY TIME Q - B - L T stock on-hand stock on-hand + on-order

8. Q SENSITIVITY OF C, R, & H H CR 2 * Q  * Q * Q X X X * Q * Q * Q Q H R C    X X X * Q X X X H CR 2 Q H R C H R C   = order quantity error fraction 1   H R C X X X

9. TVC(Q) SENSITIVITY OF C, R, AND H * HQ PR *) Q ( TC 2 HQ Q CR PR ) Q ( TC      2 *) Q ( TVC 2 * HQ * Q CR   * HQ *) Q ( TVC 2 HQ Q CR ) Q ( TVC    H R C H H R C X X X X * Q X X X H CR 2 Q           H CR 2 * Q 

10. *) Q ( TVC *) Q ( TVC X X X *) Q ( TVC *) Q ( TVC *) Q ( TVC ) Q ( TVC H R C    H R C X X X *) Q ( TVC  H R C X X X 2 * HQ * Q CR         2 HQ Q CR ) Q ( TVC   H H R C H H R C H R C X 2 X X X * Q HX X X X * Q X X CRX   fraction error TVC 1 X X X H R C   

11. TVC(Q) SENSITIVITY OF Q  * HQ *) Q ( TVC                           Q 2 Q Q Q X 1 X 2 *) Q ( TVC X X 1 2 *) Q ( TVC     Q Q 2 X * HQ X * Q CR 2 HQ Q CR ) Q ( TVC   Q factor error EOQ EOQ actual EOQ estimated X   2 *) Q ( TVC 2 * HQ * Q CR

12. *) Q ( TVC *) Q ( TVC X 1 X 2 *) Q ( TVC *) Q ( TVC *) Q ( TVC ) Q ( TVC Q 2 Q             X 2 1 X 2 X Q Q 2 Q    1 X 2 1 X Q 2 Q    fraction error TVC X 2 ) 1 X ( Q 2 Q   

13. EOQ SENSITIVITY Order quantity Q - Q* X C , X R , X H X C X R Q* X H Total variable cost TVC(Q) – TVC(Q*) X C , X R , X H  X C X R X H - 1 TVC(Q*) Total variable cost TVC(Q) – TVC(Q*) X Q (X Q – 1) 2 TVC(Q*) 2 X Q Error Fraction Error Factor Formula - 1

14. BACKORDERING INVENTORY MODEL INVENTORY LEVEL TIME Q t 2 t 3 t 1 J 0

15. TC(Q, J) = Purchase + Order + Holding + Backordering R J t and R J Q t KJt t J Q H C PQ Q R 2 2 ) ( 2 1 2 1               Q KJ Q HJ HJ HQ Q CR PR 2 2 2 2 2       Q KJ Q J JQ Q H Q CR PR 2 2 ) 2 ( 2 2 2       Q KJ Q J Q H Q CR PR 2 2 ) ( 2 2      R KJ R J Q H C PQ Q R 2 2 ) ( 2 2             

16. Q KJ Q HJ H Q CR Q J Q TC        2 2 2 ) , ( 2 2 2 2 2 K H HQ J   * J J Q TC    Q J K H H Q KJ Q HJ H         0 ) ( ) , ( H J K H H CR Q    ) ( 2 * 2 2 J K H CR Q H              0 2 ) ( 1 2 2 2 K K H H CR Q   2 * B = RL - J * Q * - J * = KQ * H + K

17. PROOF: TC(Q*, J*) = PR + KJ* 2 2 2 * * * * * 2 * 2 2 ) ( ) , ( K H KQ J Q K H HQ J K K H H CR Q Q kJ Q J Q H Q CR PR J Q TC             2 2 2 2 ) ( 2 * ) ( 2 * ) ( 2 * K H KQ H K H Q HK K K H H CR CRQ PR        2 2 * * 2 * * 2 * * * *) *, ( K H HQ Q K K H KQ Q H Q Q Q CR PR J Q TC                          

18. TC(Q*, J*) * ) ( 2 ) ( 2 2 2 2 Q K H K H HK K H HK PR             H K 2 * K H HKQ PR    ) ( * ) ( * ) ( 2 2 2 K H Q K H HK PR Q K H HK PR               * ) ( 2 2 2 2 2 2 Q K H K H HK HK K H PR             * KJ PR   TC(Q*, J*) * * K H HQ J  

19. Lower unit cost Higher holding costs Lower ordering costs Larger inventory investment Fewer stockouts Older stock Price increase hedge Slow inventory turnover QUANTITY DISCOUNTS Advantages Disadvantages

20. ALL - UNITS QUANTITY DISCOUNTS j j j j j i P P P U U U where U Q U for P U Q U for P U Q U for P P                         1 0 2 1 1 2 1 1 1 0 0 : breakpoints = unit purchase cost =

21. ORDER QUANTITY (Q) COST INVENTORY COSTS: ALL-UNITS QUANTITY DISCOUNTS U 1 U 2 TC(Q) PFQ 2 PR CR Q

22. ALL-UNITS QUANTITY DISCOUNTS CASE 1 CASE 2 CASE 3 U 1 U 1 U 1 QUANTITY TOTAL COST Decision Rule : Order the quantity with the lowest cost. Case 1: Order > U 1 Case 2: Order = U 1 Case 3: Order < U 1

23. ALL-UNITS QUANTITY DISCOUNT LOGIC Calculate the EOQ for the lowest unit cost Is the EOQ valid ? Calculate the total cost for the valid EOQ and all larger price-break quantities Calculate the EOQ for the next higher unit cost Is the EOQ valid ? Select the EOQ as the order quantity Select the order quantity with the lowest total cost Start No No Yes Yes

24. KNOWN PRICE INCREASE q Q ^ Q* Q* t a t 1 t 2 t 3 TIME QUANTITY a Special Order No Special Order

25. KNOWN PRICE INCREASE l . SPECIAL ORDER OF Q FOR TIME PERIOD (Q+q) / R Total Cost = Purchase + Holding + Order ˆ ˆ C R 2 PFq R 2 Q ˆ PF R Q ˆ PFq Q ˆ P TC 2 2 s      C R q PF 2 q R Q ˆ PF 2 Q ˆ R q PF Q ˆ Q ˆ P TC s      holding cost of Q from t 2 to t 3 holding cost of q from t 1 to t 2 holding cost of Q from t 1 to t 2 ˆ ˆ

26. II. NO SPECIAL ORDER     R PFq R Q ˆ * FQ k P Q ˆ k P TC 2 a n          * Q Q ˆ C R q PF 2 q R Q ˆ F k P 2 * Q Q ˆ k P TC a a n           * Q Q ˆ C R 2 PFq R 2 Q ˆ * FQ k P Q ˆ k P a 2 a Q       holding cost of q from t 1 to t 2 holding cost of Q* from t 2 to t 3 a C       R 2 Q ˆ a * FQ k P F k P CR / 2 a * Q Q ˆ 2 a * Q a * Q ˆ C a * Q Q ˆ C     

27. KNOWN PRICE INCREASE    Savings Cost TC TC g s n *       0 ˆ ) ( ˆ R Q PF R PFq R FQ k P k Q d dg a             2 ˆ ˆ * ) ( 2 C R Q PF Q R PFq R FQ k P k g a    2 2 ˆ 2 2 C R PFq R Q PF ˆ        ˆ ˆ 2 * ) ( ˆ ) ( 2 R Q PFq Q P R PFq R Q FQ k P Q k P a     * ) ( * ˆ q P Q k P PF kR Q a = optimum special order quantity 1               * * ˆ * 2 Q Q C g     = optimum cost savings of special order

28. KNOWN PRICE INCREASE: DERIVATION OF g* C R Q PF Q R PFq R FQ k P k g R Q PF R PFq R FQ k P k q P Q k P PF kR Q a a a                       2 ˆ ˆ ) ( * ˆ ) ( ) ( * ˆ 2 * * *  *) ( 2 2 Q C R PF                   1 * * ˆ * 2 Q Q C g   *) ( *) ˆ ( 2 2 C Q Q C C R Q PF R Q PF g    2 *) ˆ ( *) ˆ ( * 2 2 C R Q PF   2 *) ˆ ( 2

29.                                 1 * * ˆ 1 * * ˆ * ) ( ) ( ) ( * ˆ 2 2 * * Q Q C Q Q C g B q P Q k P PF kR P Q k P PF kR Q a a KNOWN PRICE INCREASE OPTIMIZATION During Regular Replenishment Before Regular Replenishment

30. PRODUCTION ORDER QUANTITY Q 1 Q B 0 t p L t 1 TIME QUANTITY (Q) - r p p - r

31. EPQ - SINGLE ITEM p r p Q r p t p ) ( ) (     MAX. INV. t p = Q/p p r p Q CR dQ Q dTC 0 2 ) H ( ) ( 2      p H r p Q Q CR PR 2 ) (     HOLDING SETUP PRODUCTION Q TC ) (    r p H CRp Q ) ( 2 *   = EPQ p HQ r p PR Q TC * ) ( *) (   

32. EPQ WITH BACKORDERING ) ( 2 * K K H r p H CRp Q    * J N RL B   ) ( ) ( * * p K H r p HQ J    ) ( ) ( * *) *, ( p K H r p K HQ PR J Q TC     * KJ PR  

33. MAKE / BUY INFLUENCING FACTORS Idle plant capacity In-house capabilities Personnel Equipment Future capabilities Economic Advantage Incremental cost Allocation of overhead Reliability of Supply Trade Relations (reciprocity) Employment stabilization Alternative resource uses

34. EPQ - MULTIPLE ITEMS Q i = R i /m* = lot size for item i R i = annual demand for item i m* = optimum number of runs (cycles) per year N = operating days per year n = number of products or items Q i / p i = run time in days per cycle for item i p i = production rate for item i in units per day N/m* = run (cycle) time in days N m* 1 2 3 4 5 1 Q 1 p 1 Q 2 p 2 Q 3 Q 4 Q 5 p 3 p 4 p 5 slack time slack time  0  n   i i i p Q 1 /

35. EPQ - MULTIPLE ITEMS m / R i t pi p i m p i / R i t pi = = = Q i Holding Setup oduction Pr ) m ( TC + + = m p i ) r i ( R i ) r i p i ( t pi - = - = MAX INV for item i p i   = = = - = n 1 i n 1 i year per runs of . no optimal C i 2 p i ) r i p i ( R i H i m * p i ) r i p i ( R i H i m 2 1 C i m R i P i n 1 i n 1 i n 1 i - + + =    = = = 0 p i ) r i p i ( R i H i m 2 2 1 C i dm ) m ( dTC n 1 i n 1 i = - - =   = =

36.  i i * m / R Q *     n 1 i i i p / Q * m N Cycle / Time Slack     n 1 i i i p R N Time Demand Time Supply       n 1 i i n 1 i i i C * m 2 R P *) m ( TC

37. FIXED ORDER INTERVAL SYSTEM Backorder/Lost Sale Issue Replenishment Order Determine Stock Position (on hand + on order - backorders) Compute Order Quantity (max. stock - stock position) Stock Available Demand Occurs Has Review Period Arrived ? Is Stock > Demand? no yes yes no no

38. FIXED ORDER INTERVAL SYSTEM QUANTITY TIME E 0 T L T L T L L

39. EOI - SINGLE ITEM TOTAL ANNUAL COST = PURCHASE + ORDER + HOLDING ) ( L T R E  = 2 ) ( RFPT T C PR T TC   = 2 ) ( 2 RFP T C dT T dTC   = = 0 2 * RFP C T = Q * = RT * = R 2C PFR = 2CR PF TC(T * ) = PR + HRT *

40. ANNUAL INVENTORY COSTS ORDER INTERVAL (T) T* COST TC(T) PFRT PR C 2 T

41. EOI - MULTIPLE ITEMS TOTAL ANNUAL COST = PURCHASE + ORDER + HOLDING ) ( L T R E i i   0 2 ) ( ) ( 1 2 P R F T nc C dT T dTC n i i i        2 ) ( ) ( 1 1 P R TF T nc C P R T TC n i i i n i i i          = n 1 i i i R P TC(T*) = ( 1 + FT*) ) ( 2 * 1 P R F nc C T n i i i     = EOI