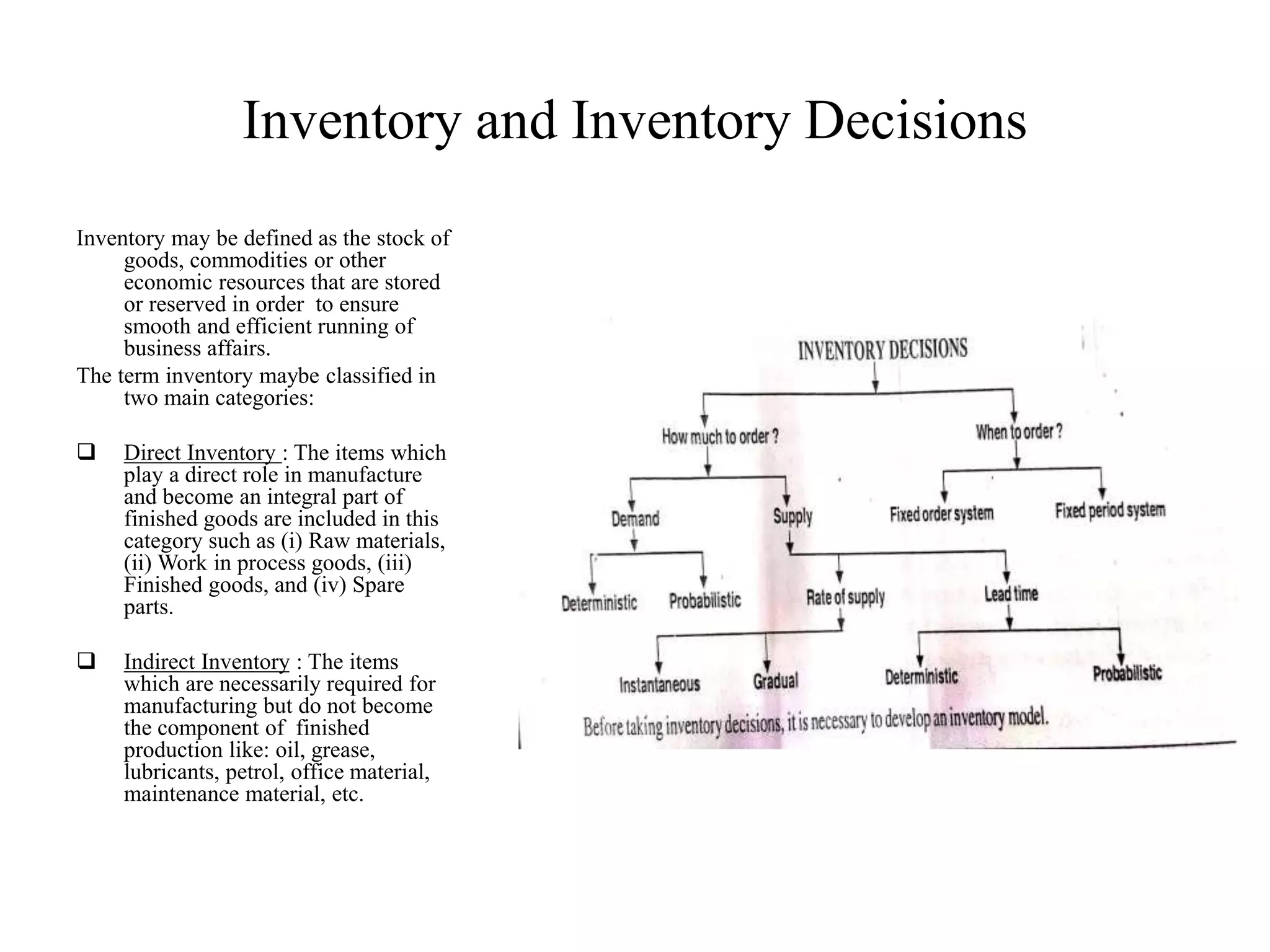
This document provides an overview of inventory management and queueing theory models. It defines key inventory terms like direct inventory, indirect inventory, holding costs, shortage costs, and setup costs. It then summarizes several deterministic inventory models that make assumptions about demand rates and allow or disallow shortages. These include the EOQ model without shortages and models that incorporate shortages. The document also introduces concepts in queueing theory, such as different states a queueing system can be in and symbols used. It provides examples of M/M/S queueing models that assume Poisson arrivals and exponential service times.



![THE EOQ MODEL WITHOUT SHORTAGE
Model I (a) : The Economic Lot Size System with Uniform Demand
Assumptions :
1) Demand is uniform at the rate of R quantity units per unit time.
2) Lead time is zero (or known exactly).
3) Production rate is infinite, i.e. production is instantaneous.
4) Shortages are not allowed.
5) Holding cost is rupees C1 per quantity per unit time.
6) Set-up cost is rupees C3 per set-up.
Derivation:
Average inventory = ½ [maximum level + minimum level] = ½ [ q + 0] = q/2.
Total inventory carrying cost per unit =average no. of units in inventory X cost of one unit X inventory carrying cost percentage
= ½ qCI = ½ qC1
Cost Equation
Total inventory costs = Total inventory carrying cost + total annual ordering costs
C(q) = ½ qC1 + (R/q) C3
Optimal EOQ
½ qC1 = (R/q) C3 => qC1 = (2R/q) C3 => q2 = 2RC3/ C1
q= (2C3R/C1)
Optimal q* (EOQ) = (2 X set-up cost X demand rate / carrying cost)](https://image.slidesharecdn.com/or1-201112134806/75/Operations-research-Inventory-Production-Managemet-and-Queueing-Theory-5-2048.jpg)

![Optimal EOQ
(q/ 2) C1T = (D/ q) C3 => q2 = 2DC3/ C1T
q= (2C3D/C1T)
Optimal q* (EOQ) = (2 X set-up cost X demand rate / carrying cost X time period)
Optimum inventory cost
Cmin = (2C1C3D/ T)
Optimum inventory cost Cmin = (2 X carrying cost X set-up cost X demand rate / time period)
Model I (c) : The Economic Lot Size System with different rates of demand in different cycles
Assumptions :
C2 = infinity, R= no. Of items required per unit time, K= no. Of items produced per unit time, t= interval between production
cycles.
Derivation :
Ordering cost = Number of orders X C3 = (R/ q) C3
Carrying cost = Average inventory X C1 X T = ½ [q/ K] (K - R) C1
Cost Equation
C(q) = ½ [q/ K] (K – R) C1 + (R/ q) C3
Optimal EOQ
½ [q/ K] (K - R )C1 = (R/ q) C3 => q2 = 2RC3/ C1(1- R/ K)
q*= (2RC3/C1(1 – R/ K))
Optimum time interval
t*= (2C3/C1R(1 – R/ K))
Optimum inventory cost
Cmin = (2C1C3R ( 1- R/ K))](https://image.slidesharecdn.com/or1-201112134806/75/Operations-research-Inventory-Production-Managemet-and-Queueing-Theory-7-2048.jpg)

![Model II (b) : The EOQ with Constant rate of Demand, Scheduling Time Variable
Assumptions :
1) t is the scheduling time period which is variable.
2) q = Rt is the order quantity per run.
Derivation :
Cost Equation C(t, z) = 1/t [ (C1z2 / 2R) + ½ (C2 / R) ( Rt – z )2 + C3 ]
Reorder time t= (2C3 (C1 + C2) / RC1C2)
Optimal EOQ q*= Rt* = (2RC3 (C1 + C2) / C1C2)
Optimum inventory cost Cmin = (2C1C3R (C2 / (C1 + C2) )
Model II (c) : The Production Lot Size with Shortages
Assumptions :
1) R units per unit time is the uniform demand rate.
2) Production rate K units per unit time is finite, K > R.
3) Shortages are allowed and backlogged.
Derivation :
Cost Equation C(t2, t3) = ½ [ (C1t22 + C2t32 ) RK + ½ (C2 / R) ( Rt – z )2 + C3 ]
Optimal EOQ q*= (2RC3 (C1 + C2) / C1C2) (1/ (1 – R/ K)) = (2RC1C3 (1-R/ K) / (C1 + C2) C2)
Optimum inventory cost Cmin = (2RC1 C2 C3 (1-R / K) / (C1 + C2) )](https://image.slidesharecdn.com/or1-201112134806/75/Operations-research-Inventory-Production-Managemet-and-Queueing-Theory-9-2048.jpg)




![Model IV (A) : (M|M|S) : (|FCFS )
The overall service rate when there are n units in the system may be obtained in the following two situations :
i. If n ≤ s, all the customers may be served simultaneously. There will be no queue, ( s – n ) number of servers
may remain idle, and then n = n, n = 0, 1, 2, …. , s.
ii. If n ≥ s, all the servers are busy, maximum number of customers waiting in the queue will be ( n – s ), then
n = s.
To obtain the system of steady state equations:
0 = -P0 + P1 for n = 0 ….. (1)
0 = - ( + n ) Pn + Pn-1 + ( n+1 ) Pn+1 for 0<n<s ….(2)
0 = - ( + s ) Pn + Pn-1 + s Pn+1 for n > s ……(3)
To solve the system of difference equations (1) , (2) , and (3) :
P0 = P0 [initially],
P1 = ( / ) P0 [from (1)],
P2 = ( / 2) P1 = ( 2 / 2! 2 ) P1 [from (2)],
P3 = ( / 3) P1 = ( 3 / 3! 3 ) P2 [from (2)],
………………………………………………..
In general, Pn = ( / n) Pn-1 = ( n / n! n ) Pn-1 { for 1 ≤ n ≤ s } [from (2)].
...............................................................................
Ps = (1/ s!) ( / )s P0
Ps+1 = (1/ s) (1/ s!) ( / )s+1 P0
Ps+2 = (1/ s2) (1/ s!) ( / )s+2 P0
In general, Pn = (1/ sn-s) (1/ s!) ( / )n P0 , [ for n ≥ s ].](https://image.slidesharecdn.com/or1-201112134806/75/Operations-research-Inventory-Production-Managemet-and-Queueing-Theory-14-2048.jpg)
![We know that, Ss-1
n=0 (Pn) + S
n=s (Pn)
P0 = S s-1
n=0 ((s)n / n!) + ( ss / s! ) (s / 1 - )
Measures :
Lq = S
n=s (n – s) Pn = Ps ( / (1 - )2 )
Ls = Lq + s + Ss-1
n=0 [(n – s) (s)n P0 / n!]
Wq = Lq / = Ps ( 1 / s(1 - )2 )
Ws = Ls / = Wq + 1 /
( L | L > 0) = [ S
n=s+1 (n – s) Pn S
n=s+1 Pn ] = 1 / (1 - )
( W | W > 0) = 1 / (s - )](https://image.slidesharecdn.com/or1-201112134806/75/Operations-research-Inventory-Production-Managemet-and-Queueing-Theory-15-2048.jpg)