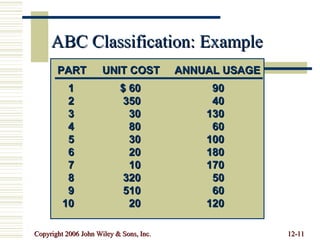
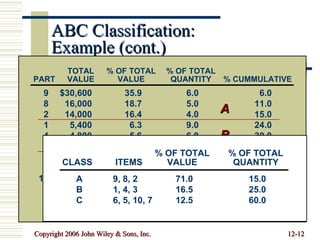
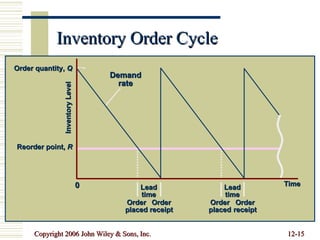
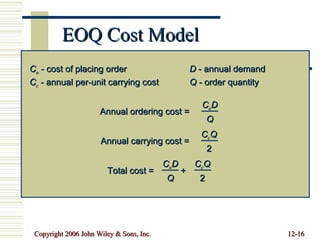
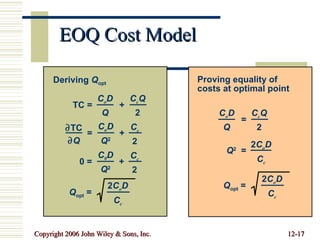
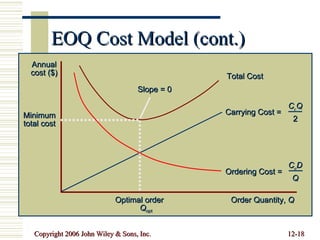
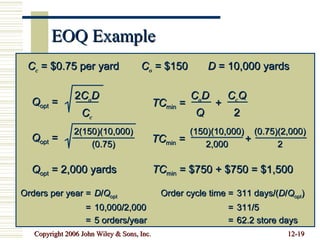
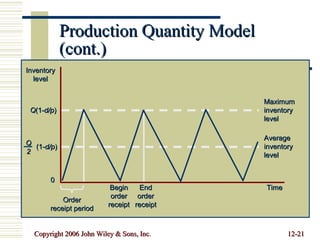
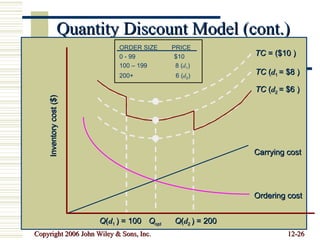
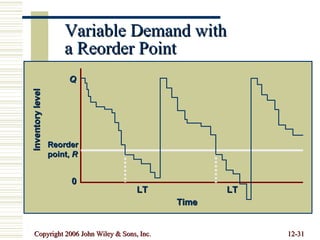
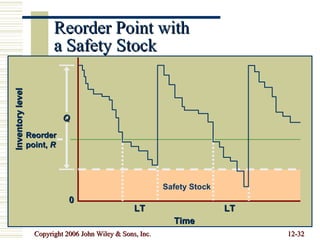
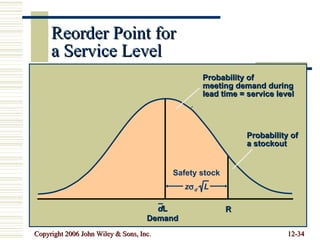
This document summarizes key concepts in inventory management including inventory control systems, economic order quantity models, reorder points, safety stocks, and periodic inventory systems. It discusses the costs of inventory like carrying costs and ordering costs. It also covers topics like ABC classification, quantity discounts, and order quantities for systems with variable demand.

1. Beni Asllani University of Tennessee at Chattanooga Inventory Management Operations Management - 5 th Edition Chapter 12 Roberta Russell & Bernard W. Taylor, III

2. Lecture Outline Elements of Inventory Management Inventory Control Systems Economic Order Quantity Models Quantity Discounts Reorder Point Order Quantity for a Periodic Inventory System

3. What Is Inventory? Stock of items kept to meet future demand Purpose of inventory management how many units to order when to order

4. Types of Inventory Raw materials Purchased parts and supplies Work-in-process (partially completed) products (WIP) Items being transported Tools and equipment

5. Inventory and Supply Chain Management Bullwhip effect demand information is distorted as it moves away from the end-use customer higher safety stock inventories to are stored to compensate Seasonal or cyclical demand Inventory provides independence from vendors Take advantage of price discounts Inventory provides independence between stages and avoids work stop-pages

6. Two Forms of Demand Dependent Demand for items used to produce final products Tires stored at a Goodyear plant are an example of a dependent demand item Independent Demand for items used by external customers Cars, appliances, computers, and houses are examples of independent demand inventory

7. Inventory and Quality Management Customers usually perceive quality service as availability of goods they want when they want them Inventory must be sufficient to provide high-quality customer service in TQM

8. Inventory Costs Carrying cost cost of holding an item in inventory Ordering cost cost of replenishing inventory Shortage cost temporary or permanent loss of sales when demand cannot be met

9. Inventory Control Systems Continuous system (fixed-order-quantity) constant amount ordered when inventory declines to predetermined level Periodic system (fixed-time-period) order placed for variable amount after fixed passage of time

10. ABC Classification Class A 5 – 15 % of units 70 – 80 % of value Class B 30 % of units 15 % of value Class C 50 – 60 % of units 5 – 10 % of value

11. ABC Classification: Example 1 $ 60 90 2 350 40 3 30 130 4 80 60 5 30 100 6 20 180 7 10 170 8 320 50 9 510 60 10 20 120 PART UNIT COST ANNUAL USAGE

12. ABC Classification: Example (cont.) Example 10.1 1 $ 60 90 2 350 40 3 30 130 4 80 60 5 30 100 6 20 180 7 10 170 8 320 50 9 510 60 10 20 120 PART UNIT COST ANNUAL USAGE TOTAL % OF TOTAL % OF TOTAL PART VALUE VALUE QUANTITY % CUMMULATIVE 9 $30,600 35.9 6.0 6.0 8 16,000 18.7 5.0 11.0 2 14,000 16.4 4.0 15.0 1 5,400 6.3 9.0 24.0 4 4,800 5.6 6.0 30.0 3 3,900 4.6 10.0 40.0 6 3,600 4.2 18.0 58.0 5 3,000 3.5 13.0 71.0 10 2,400 2.8 12.0 83.0 7 1,700 2.0 17.0 100.0 $85,400 A B C % OF TOTAL % OF TOTAL CLASS ITEMS VALUE QUANTITY A 9, 8, 2 71.0 15.0 B 1, 4, 3 16.5 25.0 C 6, 5, 10, 7 12.5 60.0

13. Economic Order Quantity (EOQ) Models EOQ optimal order quantity that will minimize total inventory costs Basic EOQ model Production quantity model

14. Assumptions of Basic EOQ Model Demand is known with certainty and is constant over time No shortages are allowed Lead time for the receipt of orders is constant Order quantity is received all at once

15. Inventory Order Cycle Demand rate Time Lead time Lead time Order placed Order placed Order receipt Order receipt Inventory Level Reorder point, R Order quantity, Q 0

16. EOQ Cost Model C o - cost of placing order D - annual demand C c - annual per-unit carrying cost Q - order quantity Annual ordering cost = C o D Q Annual carrying cost = C c Q 2 Total cost = + C o D Q C c Q 2

17. EOQ Cost Model TC = + C o D Q C c Q 2 = + C o D Q 2 C c 2  TC  Q 0 = + C 0 D Q 2 C c 2 Q opt = 2 C o D C c Deriving Q opt Proving equality of costs at optimal point = C o D Q C c Q 2 Q 2 = 2 C o D C c Q opt = 2 C o D C c

18. EOQ Cost Model (cont.) Order Quantity, Q Annual cost ($) Total Cost Carrying Cost = C c Q 2 Slope = 0 Minimum total cost Optimal order Q opt Ordering Cost = C o D Q

19. EOQ Example Orders per year = D / Q opt = 10,000/2,000 = 5 orders/year Order cycle time = 311 days/( D / Q opt ) = 311/5 = 62.2 store days C c = $0.75 per yard C o = $150 D = 10,000 yards Q opt = 2 C o D C c Q opt = 2(150)(10,000) (0.75) Q opt = 2,000 yards TC min = + C o D Q C c Q 2 TC min = + (150)(10,000) 2,000 (0.75)(2,000) 2 TC min = $750 + $750 = $1,500

20. Production Quantity Model An inventory system in which an order is received gradually, as inventory is simultaneously being depleted AKA non-instantaneous receipt model assumption that Q is received all at once is relaxed p - daily rate at which an order is received over time, a.k.a. production rate d - daily rate at which inventory is demanded

21. Production Quantity Model (cont.) Q (1- d/p ) Inventory level (1- d/p ) Q 2 Time 0 Order receipt period Begin order receipt End order receipt Maximum inventory level Average inventory level

22. Production Quantity Model (cont.) p = production rate d = demand rate Maximum inventory level = Q - d = Q 1 - Q p d p Average inventory level = 1 - Q 2 d p TC = + 1 - d p C o D Q C c Q 2 Q opt = 2 C o D C c 1 - d p

23. Production Quantity Model: Example C c = $0.75 per yard C o = $150 D = 10,000 yards d = 10,000/311 = 32.2 yards per day p = 150 yards per day Q opt = = = 2,256.8 yards 2 C o D C c 1 - d p 2(150)(10,000) 0.75 1 - 32.2 150 TC = + 1 - = $1,329 d p C o D Q C c Q 2 Production run = = = 15.05 days per order Q p 2,256.8 150

24. Production Quantity Model: Example (cont.) Number of production runs = = = 4.43 runs/year D Q 10,000 2,256.8 Maximum inventory level = Q 1 - = 2,256.8 1 - = 1,772 yards d p 32.2 150

25. Quantity Discounts Price per unit decreases as order quantity increases TC = + + PD C o D Q C c Q 2 where P = per unit price of the item D = annual demand

26. Quantity Discount Model (cont.) Q opt Carrying cost Ordering cost Inventory cost ($) Q ( d 1 ) = 100 Q ( d 2 ) = 200 TC ( d 2 = $6 ) TC ( d 1 = $8 ) TC = ($10 ) ORDER SIZE PRICE 0 - 99 $10 100 – 199 8 ( d 1 ) 200+ 6 ( d 2 )

27. Quantity Discount: Example C o = $2,500 C c = $190 per computer D = 200 QUANTITY PRICE 1 - 49 $1,400 50 - 89 1,100 90+ 900 Q opt = = = 72.5 PCs 2 C o D C c 2(2500)(200) 190 TC = + + PD = $233,784 C o D Q opt C c Q opt 2 For Q = 72.5 TC = + + PD = $194,105 C o D Q C c Q 2 For Q = 90

28. Reorder Point Level of inventory at which a new order is placed R = dL where d = demand rate per period L = lead time

29. Reorder Point: Example Demand = 10,000 yards/year Store open 311 days/year Daily demand = 10,000 / 311 = 32.154 yards/day Lead time = L = 10 days R = dL = (32.154)(10) = 321.54 yards

30. Safety Stocks Safety stock buffer added to on hand inventory during lead time Stockout an inventory shortage Service level probability that the inventory available during lead time will meet demand

31. Variable Demand with a Reorder Point Reorder point, R Q LT Time LT Inventory level 0

32. Reorder Point with a Safety Stock Reorder point, R Q LT Time LT Inventory level 0 Safety Stock

33. Reorder Point With Variable Demand R = dL + z  d L where d = average daily demand L = lead time  d = the standard deviation of daily demand z = number of standard deviations corresponding to the service level probability z  d L = safety stock

34. Reorder Point for a Service Level Probability of meeting demand during lead time = service level Probability of a stockout R Safety stock d L Demand z  d L

35. Reorder Point for Variable Demand The carpet store wants a reorder point with a 95% service level and a 5% stockout probability For a 95% service level, z = 1.65 d = 30 yards per day L = 10 days  d = 5 yards per day R = dL + z  d L = 30(10) + (1.65)(5)( 10) = 326.1 yards Safety stock = z  d L = (1.65)(5)( 10) = 26.1 yards

36. Order Quantity for a Periodic Inventory System Q = d ( t b + L ) + z  d t b + L - I where d = average demand rate t b = the fixed time between orders L = lead time  d = standard deviation of demand z  d t b + L = safety stock I = inventory level

37. Fixed-Period Model with Variable Demand d = 6 bottles per day  d = 1.2 bottles t b = 60 days L = 5 days I = 8 bottles z = 1.65 (for a 95% service level) Q = d ( t b + L ) + z  d t b + L - I = (6)(60 + 5) + (1.65)(1.2) 60 + 5 - 8 = 397.96 bottles

38. Copyright 2006 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in section 117 of the 1976 United States Copyright Act without express permission of the copyright owner is unlawful. Request for further information should be addressed to the Permission Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages caused by the use of these programs or from the use of the information herein.