Dokumen ini membahas gerak harmonik sederhana (GHS) dan aplikasinya, termasuk jenis gerakan linier dan angular, serta konsep pegas dan hukum Hooke. Selain itu, dijelaskan tentang periode, frekuensi, dan gaya pemulih pada pegas dan ayunan bandul, serta contoh soal menghitung periode dan energi kinetik. Konsep gerak harmonik dijelaskan dengan persamaan matematis untuk simpangan, kecepatan, dan energi.

1. A. Khalil Gibran Basir
Irwan Budiansyah
Sukmawati

2. Pengertian GHS
 Gerak harmonik sederhana adalah gerak bolak -
balik benda melalui suatu titik keseimbangan tertentu
dengan banyaknya getaran benda dalam setiap sekon
selalu konstan.

3. Jenis Gerak Harmonik Sederhana
Gerak Harmonik Sederhana dapat dibedakan menjadi
2 bagian, yaitu :
1. Gerak Harmonik Sederhana (GHS) Linier, misalnya
penghisap dalam silinder gas, gerak osilasi air raksa /
air dalam pipa U, gerak horizontal / vertikal dari
pegas, dan sebagainya.
2. Gerak Harmonik Sederhana (GHS) Angular, misalnya
gerak bandul/ bandul fisis, osilasi ayunan torsi, dan
sebagainya.

4. Gerak Harmonik pada Bandul
Ketika beban digantungkan
pada ayunan dan tidak
diberikan gaya, maka benda
akan dian di titik
keseimbangan B. Jika beban
ditarik ke titik A dan
dilepaskan, maka beban akan
bergerak ke B, C, lalu kembali
lagi ke A. Gerakan beban
akan terjadi berulang secara
periodik, dengan kata lain
beban pada ayunan di atas
melakukan gerak harmonik
sederhana.

5. GERAK HARMONIK PADA PEGAS
 Pegas merupakan suatu benda yang
sering kita jumpai dalam berbagai
aplikasi, dari saklar hingga sistem
suspensi kendaraan.
 Pegas amat berguna karena memiliki
kemampuan untuk direntang dan
ditekan

6. A mass is oscillating on a spring
Position in
equal time intervals:

7. Gerak vertikal pada pegas
Semua pegas memiliki
panjang alami sebagaimana
tampak pada gambar. Ketika
sebuah benda dihubungkan
ke ujung sebuah pegas,
maka pegas akan meregang
(bertambah panjang) sejauh
y. Pegas akan mencapai titik
kesetimbangan jika tidak
diberikan gaya luar (ditarik
atau digoyang)

8. Susunan Pegas
Konstanta pegas dapat berubah nilainya, apabila pegas
- pegas tersebut disusun menjadi rangkaian. Besar
konstanta total rangkaian pegas bergantung pada jenis
rangkaian pegas, yaitu rangkaian pegas seri atau
paralel

9. Seri / Deret
Gaya yang bekerja pada setiap pegas adalah sebesar F,
sehingga pegas akan mengalami pertambahan
panjang sebesar dan . Secara umum,
konstanta total pegas yang disusun seri dinyatakan
dengan persamaan :
dengan kn = konstanta
pegas ke - n.

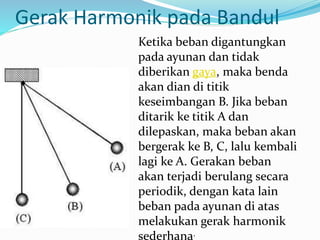
10. Paralel
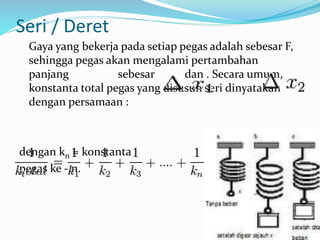
Jika rangkaian pegas ditarik dengan gaya sebesar F,
setiap pegas akan mengalami gaya tarik sebesar F1 dan
F2 , pertambahan panjang sebesar dan
. Secara umum, konstanta total pegas yang dirangkai
paralel dinyatakan dengan persamaan[5] :
ktotal = k1 + k2 + k3 +....+ kn, dengan kn = konstanta
pegas ke - n.

12. Contoh Soal
 Dua buah pegas identik dengan kostanta masing-masing
sebesar 200 N/m disusun seri seperti terlihat pada gambar
berikut.
Beban m sebesar 2 kg digantungkan
pada ujung bawah pegas. Tentukan
periode sistem pegas tersebut!
 Pembahasan
Gabungkan konstanta kedua pegas dengan susunan seri:

13. Contoh Soal
Dua buah pegas dengan
kostanta sama besar
masing-masing sebesar
150 N/m disusun secara
paralel seperti terlihat
pada gambar berikut.
Tentukan besar periode
dan frekuensi susunan
tersebut, jika massa beban
m adalah 3 kilogram!
Pembahasan
Periode susunan pegas
paralel, cari konstanta
gabungan terlebih dahulu:

14. Gaya Pemulih
Gaya pemulih dimiliki oleh setiap benda elastis yang
terkena gaya sehingga benda elastis tersebut berubah
bentuk. Gaya yang timbul pada benda elastis untuk
menarik kembali benda yang melekat padanya di sebut
gaya pemulih.
 Gaya Pemulih pada Pegas
Pegas adalah salah satu contoh benda elastis. Oleh sifat
elastisnya ini, suatu pegas yang diberi gaya tekan atau gaya
regang akan kembali pada keadaan setimbangnya mula-
mula apabila gaya yang bekerja padanya dihilangkan. Gaya
pemulih pada pegas banyak dimanfaatkan dalam bidang
teknik dan kehidupan sehari- hari. Misalnya di dalam
shockbreaker dan springbed. Sebuah pegas berfungsi
meredam getaran saat roda kendaraan melewati jalan yang
tidak rata. Pegas - pegas yang tersusun di dalam springbed
akan memberikan kenyamanan saat orang tidur

15. Hukum Hooke
Jika gaya yang bekerja pada sebuah pegas dihilangkan,
pegas tersebut akan kembali pada keadaan semula.
Robert Hooke, ilmuwan berkebangsaan Inggris
menyimpulkan bahwa sifat elastis pegas tersebut ada
batasnya dan besar gaya pegas sebanding dengan
pertambahan panjang pegas. Dari penelitian yang
dilakukan, didapatkan bahwa besar gaya pegas
pemulih sebanding dengan pertambahan panjang
pegas. Secara matematis, dapat dituliskan sebagai:
, dengan k = tetapan pegas (N /
m)
Tanda (-) diberikan karena arah gaya pemulih pada
pegas berlawanan dengan arah gerak pegas tersebut.

16. Gaya Pemulih pada Gerak
Harmonik Sederhana
Gaya Pemulih pada Pegas
k = konstanta pegas (N/m)
y = simpangan (m)
Gaya Pemulih pada Ayunan Bandul Sederhana
m = massa benda (kg)
g = percepatan gravitasi (m/s2)

17. Periode dan Frekuensi
Periode adalah waktu yg diperlukan untuk melakukan
satu kali gerak bolak-balik.
Frekuensi adalah banyaknya getaran yang dilakukan
dalam waktu 1 detik.
Untuk pegas yg memiliki konstanta gaya k yg bergetar
karena adanya beban bermassa m, periode getarnya
adalah

18. Vertical position versus time:
Period T
Period T

19. Sedangkan pada ayunan bandul sederhana, jika
panjang tali adalah l, maka periodenya adalah
 Keterangan :
 f = frekuensi pegas (Hz)
 T = periode pegas (sekon)
 k = konstanta pegas (N/m)
 m = massa (kg)

20. Contoh Soal
 Sebuah bandul matematis memiliki panjang tali 64 cm dan
beban massa sebesar 200 gram. Tentukan periode getaran
bandul matematis tersebut, gunakan percepatan gravitasi
bumi g = 10 m/s2
Pembahasan
Periode ayunan sederhana:
Dari rumus periode getaran ayunan sederhana:
Sehingga:
Catatan:
Massa beban tidak mempengaruhi periode atau frekuensi
dari ayunan sederhana (bandul matematis, conis).

21. Sebuah beban bermassa 250 gram digantung dengan
sebuah pegas yang memiliki kontanta 100 N/m
kemudian disimpangkan hingga terjadi getaran
selaras. Tentukan periode getarannya!
Pembahasan
Diketahui:
k = 100 N/m
m = 250 g = 0,25 kg
T = .....
Contoh Soal

22. Sehingga:
Dari rumus periode getaran sistem pegas:

23. Simpangan Gerak Harmonik Sederhana
y = simpangan (m)
A = amplitudo (m)
ω = kecepatan sudut (rad/s)
f = frekuensi (Hz)
t = waktu tempuh (s)
Jika pada saat awal benda pada posisi θ0, maka
Besar sudut (ωt+θ0) disebut sudut fase (θ), sehingga
φ disebut fase getaran dan
Δφ disebut beda fase.

24. Contoh Soal
Sebuah benda bergetar hingga membentuk suatu
gerak harmonis dengan persamaan
y = 0,04 sin 20π t
dengan y adalah simpangan dalam satuan meter, t
adalah waktu dalam satuan sekon. Tentukan beberapa
besaran dari persamaan getaran harmonis tersebut:
a) amplitudo
b) frekuensi
c) periode
d) simpangan maksimum
e) simpangan saat t = 1/60 sekon
f) simpangan saat sudut fasenya 45°
g) sudut fase saat simpangannya 0,02 meter

25. Pembahasan
Pola persamaan simpangan
gerak harmonik diatas adalah
y = A sin ωt
ω = 2π f atau
2π
ω = _____
T
a) amplitudo atau A
y = 0,04 sin 20π t
↓
A = 0,04 meter
b) frekuensi atau f
y = 0,04 sin 20π t
↓
ω = 20π
2πf = 20π
c) periode atau T
T = 1/f
T = 1/10 = 0,1 s
d) simpangan maksimum atau
ymaks
y = A sin ωt
y = ymaks sin ωt
y = 0,04 sin 20π t
↓
y = ymaks sin ωt
ymaks = 0,04 m
(Simpangan maksimum tidak
lain adalah amplitudo)

26. e) simpangan saat t = 1/60 sekon
y = 0,04 sin 20π t
y = 0,04 sin 20π (1/60)
y = 0,04 sin 1/3 π
y = 0,04 sin 60° = 0,04 × 1/2√3 = 0,02 √3 m
f) simpangan saat sudut fasenya 45°
y = A sin ωt
y = A sin θ
dimana θ adalah sudut fase, θ = ωt
y = 0,04 sin θ
y = 0,04 sin 45° = 0,04 (0,5√2) = 0,02√2 m
g) sudut fase saat simpangannya 0,02 meter
y = 0,04 sin 20π t
y = 0,04 sin θ
0,02 = 0,04 sin θ
sin θ = 1/2
θ = 30°

27. Contoh Soal 2
 Diberikan sebuah persamaan simpangan gerak
harmonik
y = 0,04 sin 100 t
Tentukan:
a) persamaan kecepatan
b) kecepatan maksimum
c) persamaan percepatan
Pembahasan
a) persamaan kecepatan
Berikut berurutan rumus simpangan, kecepatan dan
percepatan:

28. Pembahasan
a) persamaan kecepatan
Berikut berurutan rumus
simpangan, kecepatan dan
percepatan:
 y = A sin ωt
 ν = ωA cos ω t
 a = − ω2 A sin ω t
Ket:
y = simpangan (m)
ν = kecepatan (m/s)
a = percepatan (m/s2)
Dari y = 0,04 sin 100 t
ω = 100 rad/s
A = 0,04 m
 sehingga:
ν = ωA cos ω t
ν = (100)(0,04) cos 100 t
ν = 4 cos 100 t
b) kecepatan maksimum
 ν = ωA cos ω t
 ν = νmaks cos ω t
 νmaks = ω A
ν = 4 cos 100 t
↓
νmaks = 4 m/s
c) persamaan percepatan
a = − ω2 A sin ω t
a = − (100)2 (0,04) sin 100 t
a = − 400 sin 100 t

29. KECEPATAN (v)
Jika simpangan menunjukkan posisi suatu
benda, maka kecepatan merupakan turunan
pertama dari posisi.
Hubungan kecepatan dengan simpangan
harmonik

30. Contoh Soal
 Sebuah balok bermassa 0,5
kg dihubungkan dengan
sebuah pegas ringan dengan
konstanta 200 N/m.
Kemudian sistem tersebut
berosilasi harmonis. Jika
diketahui simpangan
maksimumnya adalah 3 cm,
maka kecepatan maksimum
adalah....
A. 0,1 m/s
B. 0,6 m/s
C. 1 m/s
D. 1,5 m/s
E. 2 m/s
Pembahasan
Data :
m = 0,5 kg
k = 200 N/m
ymaks = A = 3 cm = 0,03 m
vmaks = ......
 Periode getaran pegas :
T = 2π √(m/k)
T = 2π √(0,5/200) = 2π√(1/400)
= 2π (1/20) = 0,1 π sekon
vmaks = ω A
2π
vmaks= ____ x A
T
2π
vmaks = ______ x (0,03) = 0,6
m/s
0,1 π

31. PERCEPATAN (a)
 Jika simpangan menunjukkan posisi suatu
benda, maka kecepatan merupakan turunan
pertama dari kecepatan terhadap waktu.
 Hubungan percepatan dengan simpangan
harmonik
Ket:
ω : kecepatan sudut (rad/s)
A : amplitudo (m)
a : percepatan

32. Energi pada Gerak Harmonik
SederhanaEnergi kinetik benda yg melakukan gerak harmonik
sederhana, misalnya pegas, adalah
Karena k = mω2, diperoleh
Energi potensial elastis yg tersimpan di dalam pegas
untuk setiap perpanjanganya adalah

33. Jika gesekan diabaikan, energi total atau energi
mekanik pada getaran pegas adalah
Keterangan:
Em : Energi Mekanik
Ep : Energi Potensial
Ek : Energi Kinetik
A : Ampitudo
m : Massa
ω : kecepatan sudut (rad/s)

34. Contoh Soal
 Sebuah benda yang massanya 200 gram bergetar
harmonik dengan periode 0,2 sekon dan
amplitudo 2 cm. Tentukan :
a) besar energi kinetik saat simpangannya 1 cm
b) besar energi potensial saat simpangannya 1 cm
c) besar energi total
 Pembahasan

35. Data dari soal:
m = 200 g = 0,2 kg
T = 0,2 s → f = 5 Hz
A = 2 cm = 0,02 m = 2 x 10-2 m
a) besar energi kinetik saat simpangannya 1 cm
y = 1 cm = 0,01 m = 10-2 m
Ek = ....
b) besar energi potensial saat simpangannya 1 cm
c) besar energi total

36. Contoh Soal
 Tentukan besarnya sudut fase saat :
a) energi kinetik benda yang bergetar sama dengan energi
potensialnya
b) energi kinetik benda yang bergetar sama dengan
sepertiga energi potensialnya
Pembahasan
a) energi kinetik benda yang bergetar sama dengan energi
potensialnya
Ek = Ep
1/2 mν2 = 1/2 ky2
1/2 m (ω A cos ω t)2 = 1/2 mω2 (A sin ω t)2
1/2 m ω2 A2 cos2 ω t = 1/2 mω2 A2 sin2 ω t
cos2 ω t = sin2 ω t
cos ω t = sin ω t
tan ω t = 1
ωt = 45°

37.  Energi kinetik benda yang bergetar sama dengan
energi potensialnya saat sudut fasenya 45°
b) energi kinetik benda yang bergetar sama
dengan sepertiga energi potensialnya
Ek = 1/3 Ep
1/2 mν2 =1/3 x 1/2 ky2
1/2 m (ω A cos ω t)2 = 1/3 x 1/2 mω2 (A sin ω t)2
1/2 m ω2 A2 cos2 ω t = 1/3 x 1/2 mω2 A2 sin2 ω t
cos2 ω t = 1/3 sin2 ω t
cos ω t = 1/√3 sin ω t
sin ω t / cos ω t = √3
tan ω t = √3
ω t = 60°
Energi kinetik benda yang bergetar sama dengan
sepertiga energi potensialnya saat sudut fasenya
60°