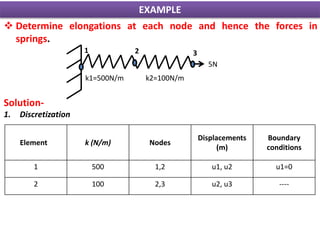
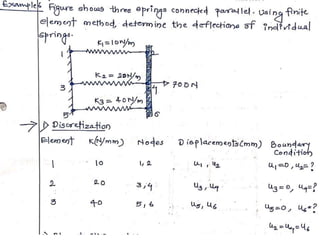
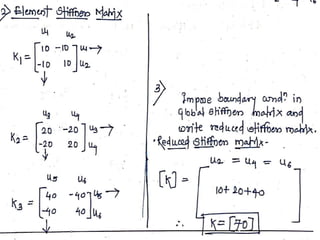
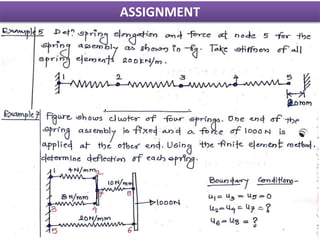
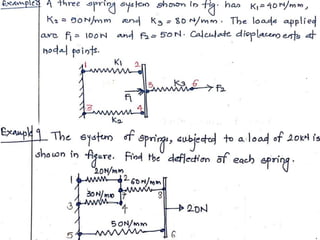
This document presents a finite element analysis of a spring assembly. It contains the following key points: 1) It describes a finite element model of a two-spring assembly, where each spring is modeled as a 1D element with one degree of freedom (axial displacement) at each node. 2) It presents the stiffness matrix formulation for a two-node spring element and shows how the element stiffness matrices are assembled into a global stiffness matrix. 3) It shows an example problem where the displacements and forces in each spring are determined when a 5N force is applied to the free end of the assembly. The analysis involves forming the stiffness matrix, applying boundary conditions, solving the equilibrium equations, and calculating the

1. FINITE ELEMENT ANALYSIS OF
SPRING ASSEMBLY
BY-
Ms. JAPE ANUJA S.
ASSISTANT PROFESSOR,
CIVIL ENGINEERING DEPARTMENT,
SRES, SANJIVANI COLLEGE OF ENGINEERING,
KOPARGAON-423603.
MAID ID: anujajape@gmail.com
japeanujacivil@sanjivani.org.in

2. FINITE ELEMENT ANALYSIS OF SPRING ASSEMBLY
• Springs are 1D structures subjected to axial force only.
• The degree of freedom at each node is one i.e. axial displacement.
• Stiffness matrix for spring element having stiffness constant k is given below which can be
obtained by giving unit displacement one by one at each node.
• Let consider a two noded spring element with ui and uj displacements at each nodes.
• Let unit displacement at node i
k11=k
k21=-k
• Let unit displacement at node j
k12=k
k22=-k
11 12
21 22
1 1
1 1
k k
K
k k
K k
 
  
 
 
   

3. FINITE ELEMENT ANALYSIS OF SPRING ASSEMBLY
    K f 
 f

4. EXAMPLE
 Determine elongations at each node and hence the forces in
springs.
Solution-
1. Discretization
5N
k1=500N/m k2=100N/m
1 2 3
Element k (N/m) Nodes
Displacements
(m)
Boundary
conditions
1 500 1,2 u1, u2 u1=0
2 100 2,3 u2, u3 ----

5. 2. Element stiffness matrices
u1 u2 u2 u3
3. Global stiffness matrix
u1 u2 u3
4. Reduced stiffness matrix
Imposing the boundary condition u1=0, i.e. eliminate first row and first column
Therefore reduced stiffness matrix is
 1 1
1 1 500 500 1
1 1 500 500 2
u
K k
u
    
        
 2 2
1 1 100 100 2
1 1 100 100 3
u
K k
u
    
        
 
500 500 0 1
500 600 100 2
0 100 100 3
u
K u
u
 
    
  
 
600 100
100 100
K
 
   

6. 5. Determine unknown joint displacements
Applying Equation of Equilibrium
6. Calculation of spring force
For Spring 1
(u1=0 and u2=0.01)
For Spring 2, and
    
600 100 2 0
100 100 3 5
K f
u
u
 
     
         
     
 
 
1 11
1
2
1
2
500 500 1
500 500 2
5
5
K f
fu
fu
f N T
f N T
 
     
         
 

 2 5f N T  3 5f N T
 
 
2 0.01
3 0.06
u m
u m
  
 
5N5N
5N5N

10. ASSIGNMENT

11. ASSIGNMENT