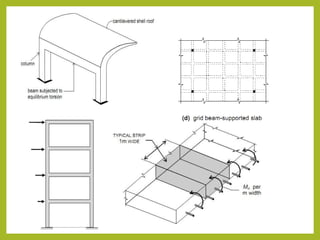
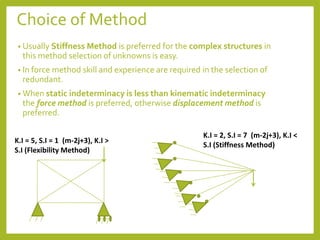
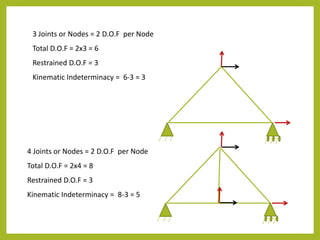
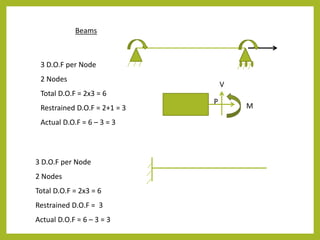
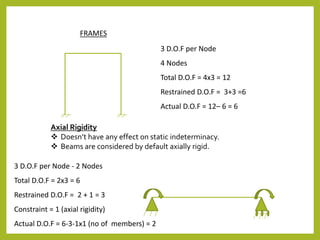
The document discusses the matrix method of structural analysis. Key points include: - The matrix method uses stiffness or flexibility matrices to relate forces and displacements in a structure. - Structures can be classified based on their dimensions and how they carry loads. Common types include beams, trusses, frames, arches, cables and plates. - Degree of freedom, boundary conditions, and compatibility must be considered. The stiffness method is commonly used for complex structures. - Beam element stiffness matrices are developed relating the forces and moments to the displacements and rotations at nodes. - Properties of stiffness matrices are discussed along with developing the load matrix and solving for displacements.

1. PPT
ADVANCED STRUCTURAL
ANALYSIS
CE(PE)704B
ContinuousAssessment 1
(CA1):
Responsible Teacher
Mr. Arindam Ghosh
COLLEGE / INSTITUTION: HEMNALINI
MEMORIAL COLLEGE OF ENGINEERING
AFFILIATED BY MAKAUT
NAME : BIJOY SARKAR
ROLL NO : 34301319001
REGISTRATION NO : 025319 OF 2019-
20
PROGRAM: BACHELOR OF TECHNOLOGY
IN CIVIL ENGINEERING

2. MATRIX METHOD OF
STRUCTURAL ANALYSIS
THE MATRIX METHOD IS A STRUCTURAL ANALYSIS METHOD USED AS A
FUNDAMENTAL PRINCIPLE IN MANY APPLICATIONS IN CIVIL ENGINEERING. THE
METHOD IS CARRIED OUT, USING EITHER A STIFFNESS MATRIX OR A
FLEXIBILITY MATRIX.

3. Classification of Structures..
• The primary function of structure is to safely transfer the external
loads acting on it to the foundation.
• Structures can be classified in many different ways
• Dimension :
1 – D –>one dimension say length is very large when compared
with other two. Ex: Beams,Trusses…
2- D or Surface Structure-> Here length & Breadth are large compared to
thickness.
Ex: slabs, Deep Beams, Shells, walls, plates…
3-D or Solid Structure-> here all the three Dimensions L,b,d are prominent
Ex: Dams, foundation , retaining walls etc..

4. • Structures can be classified based on the way they carry loads:
• Beam - carry their loads by developing B.M & S.F
• Truss – Carry loads developing axial forces like tension and
compression.
• Frames - carry loads by axial force, B.M & S.F.
• Arches – carry load by compression & bending
• Cables – carry loads by developing axial tension
• Two way Grids – are subjected to both bending and twisting.
• Thin Plates – are subjected to bending and twisting.
• Thin Shells –Transfer stress as membrane stresses.
• Analysis of any structure involves finding out the displacements &
internal forces

6. • Any method is SA should satisfy –
• 1. Equilibrium
• 2. Compatibility - --- these condition refer to the continuity of
displacement throughout the structure and are some times referred
as geometrical conditions.
Displacements should be compactable with support conditions for
example there can be no translation and rotaion at a fixed support.
Compatibility condition should be satisfied at all point in a structure.
• 3. Stress – Strain Law --- Stress ∞(Strain )n
• 4. Boundary condition

7. Kinematic Indeterminacy (Degree of Freedom)
Minimum independent quantities (displacement quantities like
deflection and rotation ) - required to define the displaced geometry of
the structure.
No points can go anywhere so kinematic indeterminacy = 0
Or Kinematically Determinate

8. 3 Joints or Nodes = 2 D.O.F per Node
Total D.O.F = 2x3 = 6
Restrained D.O.F = 3
Kinematic Indeterminacy = 6-3 = 3
4 Joints or Nodes = 2 D.O.F per Node
Total D.O.F = 2x4 = 8
Restrained D.O.F = 3
Kinematic Indeterminacy = 8-3 = 5

9. 3 D.O.F per Node
2 Nodes
Total D.O.F = 2x3 = 6
Restrained D.O.F = 2+1 = 3
Actual D.O.F = 6 – 3 = 3
Beams
V
M
P
3 D.O.F per Node
2 Nodes
Total D.O.F = 2x3 = 6
Restrained D.O.F = 3
Actual D.O.F = 6 – 3 = 3

10. FRAMES
3 D.O.F per Node
4 Nodes
Total D.O.F = 4x3 = 12
Restrained D.O.F = 3+3 =6
Actual D.O.F = 12– 6 = 6
Axial Rigidity
 Doesn’t have any effect on static indeterminacy.
 Beams are considered by default axially rigid.
3 D.O.F per Node - 2 Nodes
Total D.O.F = 2x3 = 6
Restrained D.O.F = 2 + 1 = 3
Constraint = 1 (axial rigidity)
Actual D.O.F = 6-3-1x1 (no of members) = 2

11. Frames
3 D.O.F per Node - 2 Nodes
Total D.O.F = 4x3 = 12
Restrained D.O.F = 6
Constraint = 1 (axial rigidity)
Actual D.O.F = 12-6-1x3 (no of members) = 3
The supports are rigid vertical deflection = 0
Horizontal Deflection != 0 it’s a constant
So D.O.F = 2 Rotation + 1 Hor. Deflection
= 3
=0 =0

12. Matrix method of SA
• In an elastic structure, there are 2 set of interrelated quantities –
forces (incl. moments, stresses, reaction etc..) & displacements
(incl. rotations, strains, twist etc..).
• The behavior of a structure can largely be defined by defining
the force – displacement relationship in the form of matrix.
Two Methods :
Flexibility Method Stiffness Method
1. Force Method Displacement Method
2. Basic Unknowns are the redundant
forces
Basic unknowns are
displacement of joints
3. [Δ] = [F][P]
[Disp Matrix] = [Flexibility Matrix] x
[Load Matrix]
[K] [Δ] = [P]
[Stiffness Matrix] x[Disp. Matrix]
= [Load Matrix]

13. Choice of Method
• Usually Stiffness Method is preferred for the complex structures in
this method selection of unknowns is easy.
• In force method skill and experience are required in the selection of
redundant.
• When static indeterminacy is less than kinematic indeterminacy
the force method is preferred, otherwise displacement method is
preferred.
K.I = 5, S.I = 1 (m-2j+3), K.I >
S.I (Flexibility Method)
K.I = 2, S.I = 7 (m-2j+3), K.I <
S.I (Stiffness Method)

14. Advantages of Matrix Method…
• The flexibility and stiffness method provides a systematic method for
analysis of large structures with high degree of static and kinematic
indeterminacy.
• The matrix approach can be easily converted to a computer
programs which can be used for obtaining results.
• Matrix method is a generalized method takes into account of all he
parameters that may influence a structural system.
Disadvantage:
Large number of simultaneous equation makes the analysis tedious
or manual computations. So we require computing power.
Further the analyst doesn't get an adequate feel for the flow of
forces & structural behavior as in classical methods

15. Stiffness Method of Analysis For Beam
• In order to apply stiffness method to beams, we must first determine
how to sub - divide the beam into its component .
• In general each element must be free from load and have prismatic
cross-section.
• For this reason the nodes of each element are located at a support or
at points where the c/s area suddenly changes, or where the the
vertical or rotational displacement at a point is to determined.
• Beam Element Stiffness Matrix
• Consider a beam element of uniform c/s area.The longitudinal
axis of the element lies along the x-axis , the element has constant I ,
modulus of elasticity E and Length L.

16. M1 , Θ1
M2, Θ2
2
1
F1 , δ1
F2 , δ2
L, EI
4
2
1
3
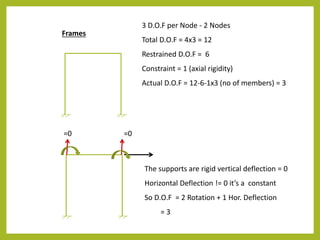
D.O.F
[K] [Δ] = [P]
Stiffness matrix K is a 4x4 matrix with stiffness coefficients.
Stiffness coefficient Kij means the force developed at ith D.O.F due to unit
displacement at jth D.O.F such that other D.O.Fs are arrested or fixed.

17. 4
2
1 D.O.F
6EI/L2 1
6EI/L2
12EI/L3
12EI/L3
K11 = force in 1 due to 1 = + 12EI/L3 (
)
K21 = - 6EI/L2
K31 = -12EI/L3
K41 = - 6EI/L2
2EI/L
6EI/L2
6EI/L2
4EI/L
1
MAB = MFAB + 2EI/L(2θA+ θB ) = 4EI/L
MBA = MFBA + 2EI/L(θA+ 2θB ) = 2EI/L
θA = 1
K12 = -6EI/L2
K22 = 4EI/L
K32 = +6EI/L2
K42 = 2EI/L
3

18. K13 = force in 1 due to 3 = -12EI/L3
K23 = + 6EI/L2
K33 = +12EI/L3
K43 = + 6EI/L2
6EI/L2
4EI/L
1
2EI/L
K14 = -6EI/L2
K24 = 2EI/L
K34 = +6EI/L2
K44 = 4EI/L

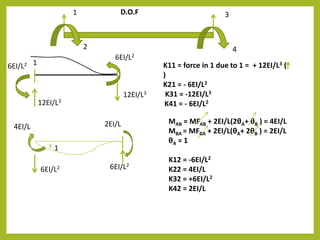
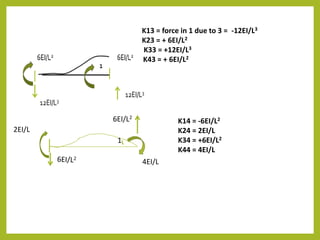
19. 1 2 3 4
K11 K12 K13 K14 1
K21 K22 K23 K24 2
K31 K32 K33 K34 3
K41 K42 K43 K44 4
[
Stiffness Matrix [K]
For a simple beam
element =
F1 = K11. δ1 + K12 . Θ1 + K13. δ2 + K14. Θ2
M1 = K21. δ1 + K22 . Θ1 + K23. δ2 + K24. Θ2
F2 = K31. δ1 + K32 . Θ1 + K33. δ2 + K34. Θ2
M2 = K41. δ1 + K42 . Θ1 + K43. δ2 + K44. Θ2
F1
M1
F2 =
M2
[ K11 K12 K13 K14
K21 K22 K23 K24
K31 K32 K33 K34
K41 K42 K43 K44
[
δ1
Θ1
δ2
Θ2
[
Load Matrix
Displacement Matrix
12EI/L3 -6EI/L2 -12EI/L3 -6EI/L2
-6EI/L2 4EI/L 6EI/L2 2EI/L
-12EI/L3 6EI/L2 12EI/L3 6EI/L2
-6EI/L3 2EI/L 6EI/L2 4EI/L
[
=

20. Properties of stiffness matrix
• Symmetric Square Matrix of order n , n is number of coordinates
chosen for solution of problem
• The diagonal elements are +ve
• The element stiffness matrix is singular i.e determinant = 0 , hence
inverse cannot be obtained.
• The third row is of same magnitudes of first row but opposite in sign i.e
F1 = -F2
Load matrix [P]
The loads applied are transformed to equivalent joint loads [EJL] or
nodal loads.
It can be obtained = Joint load matrix – Support Reaction Matrix
[P] = [Pj] – [PL]

21. C
P P
A
B
+PL/8
MBC
MCB
PL/2
P
-PL/8 -PL/8
+ PL/8
PL/2 + PL/2
PL/2
2
3
1 5
6
0 1
0 2
[Pj] = -P 3
0 4
0 5
0 6
+PL/2
-PL/8
[PL] = PL/2 +PL/2
PL/8 + -PL/8
PL/2
+PL/8
[P] = [Pj] – [PL]
LOAD MATRIX
[ [
4

22. Stiffness of a beam subjected to 2 Clockwise moments at
the two ends
A
M A
φA
B
1
D.O.F
2
2EI/L
4EI/L
1
MAB = MFAB + 2EI/L(2θA+ θB ) = 4EI/L
MBA = MFBA + 2EI/L(θA+ 2θB ) = 2EI/L
θA = 1
K11 = 4EI/L
K12 = 2EI/L
M B
2 – D.O.F
K Matrix = 2x2

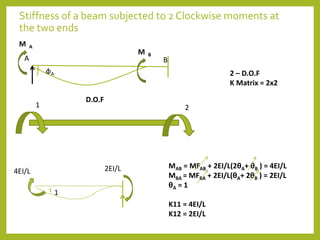
23. 4EI/L
1
2EI/L K21 = 2EI/L
K22 = 4EI/L
Stiffness Matrix [K] = K11 K12 = 4EI/L 2EI/L
K21 K22 2EI/L 4EI/L
[ [
RELATION BETWEEN STIFFNESS AND FLEXIBILITY MATRIX
[Δ] = [F][P]  [Disp Matrix] = [Flexibility Matrix] x [Load Matrix] ----- > 1
[K] [Δ] = [P]  [Stiffness Matrix] x[Disp. Matrix] = [Load` Matrix] ---------- >2
Eq 1 x [F]
-1
[F]
-1
[Δ] = [F]
-1
[F][P]
[F]
-1
[Δ] = [P]
So , [F]
-1
= [K]