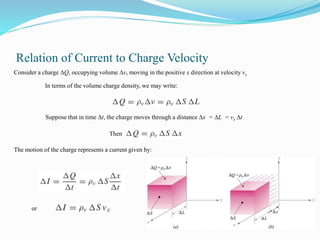
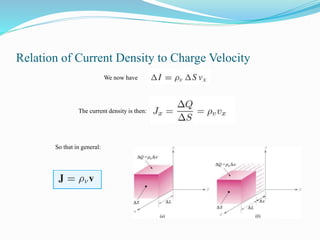
1. The document discusses conductors, dielectrics, current density, polarization, and electric susceptibility. It defines key concepts like current, current density, polarization field, dielectric constant, and boundary conditions for electric fields. 2. Conductors allow free electron flow while insulators have a large band gap; semiconductors have a small gap allowing electron excitation. Current density relates to charge velocity and conductivity. 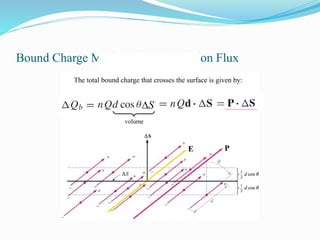3. Dielectrics have bound electric dipoles that contribute to polarization. The polarization field depends on dipole density and alignment with the electric field. Boundary conditions require continuous tangential E and normal D fields.

1. Chapter 5:
Conductors and Dielectrics

2. Current and Current Density
Current is a flux quantity and is defined as:
Current density, J, measured in Amps/m2 , yields current in Amps when
it is integrated over a cross-sectional area. The assumption would be
that the direction of J is normal to the surface, and so we would write:

3. Current Density as a Vector Field
n
In reality, the direction of current flow may not be normal to the surface in question, so we treat
current density as a vector, and write the incremental flux through the small surface in the usual way:
where S = n da
Then, the current through a large surface
is found through the flux integral:

4. Relation of Current to Charge Velocity
Consider a charge Q, occupying volume v, moving in the positive x direction at velocity vx
In terms of the volume charge density, we may write:
Suppose that in time t, the charge moves through a distance x = L = vx t
Then
or
The motion of the charge represents a current given by:

5. Relation of Current Density to Charge Velocity
We now have
The current density is then:
So that in general:

6. Continuity of Current
Qi(t)
Suppose that charge Qi is escaping from a volume through
closed surface S, to form current density J. Then the total
current is:
where the minus sign is needed to produce positive outward
flux, while the interior charge is decreasing with time.
We now apply the divergence theorem:
so that
or
The integrands of the last expression
must be equal, leading to the
Equation of Continuity

7. Energy Band Structure in Three Material Types
a) Conductors exhibit no energy gap between valence and conduction bands so electrons move freely
b) Insulators show large energy gaps, requiring large amounts of energy to lift electrons into the conduction band
When this occurs, the dielectric breaks down.
c) Semiconductors have a relatively small energy gap, so modest amounts of energy (applied through heat, light,
or an electric field) may lift electrons from valence to conduction bands.

8. Electron Flow in Conductors
Free electrons move under the influence of an electric field. The applied force on an electron
of charge Q = -e will be
When forced, the electron accelerates to an equilibrium velocity, known as the drift velocity:
where e (positive value)is the electron mobility, expressed in units of m2/V-s. The drift velocity is
used to find the current density through:
From which we identify the conductivity=>
for the case of electron flow :
The expression:
is Ohm’s Law in point form
S/m
In a semiconductor, we have hole current as well, and
where ρe is the free-electron charge density, a negative value

9. Resistance
Consider the cylindrical conductor shown here, with voltage V applied across the ends. Current flows
down the length, and is assumed to be uniformly distributed over the cross-section, S.
First, we can write the voltage and current in the cylinder in terms of field quantities:
Using Ohm’s Law:
We find the resistance of the cylinder:
a b
Non uniform field

10. Electrostatic Properties of Conductors
1. Charge can exist only on the surface as a surface charge density, s -- not in the interior.
2. Electric field cannot exist in the interior, nor can it possess a tangential component at the surface
(as will be shown next slide).
3. It follows from condition 2 that the surface of a conductor is an equipotential.
s
+
+
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+ +
+
+
+
E
solid conductor
Electric field at the surface
points in the normal direction
E = 0 inside
Consider a conductor, on
which excess charge has been placed

11. Tangential Electric Field Boundary Condition
conductor
Free space
n
Over the rectangular integration path, we use
To find:
or
These become negligible as h approaches zero.
Therefore
More formally:

12. Boundary Condition for the Normal Component of D
n
Free space
conductor
s
Gauss’ Law is applied to the cylindrical surface shown below:
This reduces to: as h approaches zero
Therefore
More formally:

13. Summary
At the surface:
Tangential E is zero
Normal D is equal to the surface charge density
• Taking the cross product or the dot product of either field quantity with n gives the tangential or
the normal component of the field, respectively.
Using these three principles, there are a number of quantities that may be calculated at a conductor
boundary, given a knowledge of the potential field

14. Method of Images
The Theorem of Uniqueness states that if we are given a configuration of charges and boundary conditions,
there will exist only one potential and electric field solution.
In the electric dipole, the surface along the plane of symmetry is an equipotential with V = 0.
The same is true if a grounded conducting plane is located there.
So the boundary conditions and charges are identical in the upper half spaces of both configurations
(not in the lower half).
In effect, the positive point charge images across the conducting plane, allowing the conductor to be
replaced by the image. The field and potential distribution in the upper half space is now found much
more easily!

15. Forms of Image Charges
Each charge in a given configuration will have its own image

16. Example
let us find the surface charge density at P(2, 5, 0) on the conducting plane z = 0 if there is a line charge of
30 nC/m located at x = 0, z = 3, as shown in Figure 5.8a. We remove the plane and install an image line
charge of −30 nC/m at x = 0, z = −3

17. Electric Dipole and Dipole Moment
Q
d p = Qd ax
In dielectric, charges are held in position (bound), and ideally there are no free charges that can move
and form a current. Atoms and molecules may be polar (having separated positive and negative charges),
or may be polarized by the application of an electric field.
Consider such a polarized atom or molecule, which possesses a dipole moment, p, defined as the charge
magnitude present, Q, times the positive and negative charge separation, d. Dipole moment is a vector
that points from the negative to the positive charge.

18. Model of a Dielectric
A dielectric can be modeled as an ensemble of bound charges in free space, associated with
the atoms and molecules that make up the material. Some of these may have intrinsic dipole moments,
others not. In some materials (such as liquids), dipole moments are in random directions.

19. Polarization Field
[dipole moment/vol]
or
[C/m2]
v

The number of dipoles is
expressed as a density, n
dipoles per unit volume.
The Polarization Field of the
medium is defined as:

20. Polarization Field (with Electric Field Applied)
E
Introducing an electric field may increase the charge separation in each dipole, and possibly re-orient dipoles so that
there is some aggregate alignment, as shown here. The effect is small, and is greatly exaggerated here!
The effect is to increase P.
= np
if all dipoles are identical

21. Migration of Bound Charge
E
Consider an electric field applied at an angle  to a surface normal as shown. The resulting
separation of bound charges (or re-orientation) leads to positive bound charge crossing upward
through surface of area S, while negative bound charge crosses downward through the surface.
Dipole centers (red dots) that lie within the range (1/2) d cos above or below
the surface will transfer charge across the surface.

22. Bound Charge Motion as a Polarization Flux
E
The total bound charge that crosses the surface is given by:
S
volume
P

23. Polarization Flux Through a Closed Surface
The accumulation of positive bound charge within a closed
surface means that the polarization vector must be pointing
inward. Therefore:
S
P
+
+
+ +
-
-
-
-
qb

24. Bound and Free Charge
Now consider the charge within the closed surface
consisting of bound charges, qb , and free charges, q.
The total charge will be the sum of all bound and free
charges. We write Gauss’ Law in terms of the total
charge, QT as:
where
QT = Qb + Q
bound charge
free charge
S
P
+
+
+ +
qb
+
+
+
+
E
q
QT

25. Gauss Law for Free Charge
QT = Qb + Q
We now have:
and
where
combining these, we write:
we thus identify: which we use in the familiar form
of Gauss’ Law:

26. Charge Densities
Taking the previous results and using the divergence theorem, we find the point form expressions:
Bound Charge:
Total Charge:
Free Charge:

27. Electric Susceptibility and the Dielectric Constant
A stronger electric field results in a larger polarization in the medium. In a linear medium, the relation
between P and E is linear, and is given by:
where e is the electric susceptibility of the medium.
We may now write:
where the dielectric constant, or relative permittivity is defined as:
Leading to the overall permittivity of the medium: where

28. Isotropic vs. Anisotropic Media
In an isotropic medium, the dielectric constant is invariant with direction of the applied electric field.
This is not the case in an anisotropic medium (usually a crystal) in which the dielectric constant will vary
as the electric field is rotated in certain directions. In this case, the electric flux density vector components
must be evaluated separately through the dielectric tensor. The relation can be expressed in the form:

29. Boundary Condition for Tangential Electric Field
Region 1
Region 2
n
2
1
We use the fact that E is conservative:
So therefore:
Leading to:
More formally:

30. Boundary Condition for Normal Electric Flux Density
n
Region 1
1
Region 2
2
We apply Gauss’ Law to the cylindrical volume shown here,
in which cylinder height is allowed to approach zero, and there
is charge density s on the surface:
The electric flux enters and exits only through the bottom and top surfaces, respectively.
s
From which:
and if the charge density is zero:
More formally: