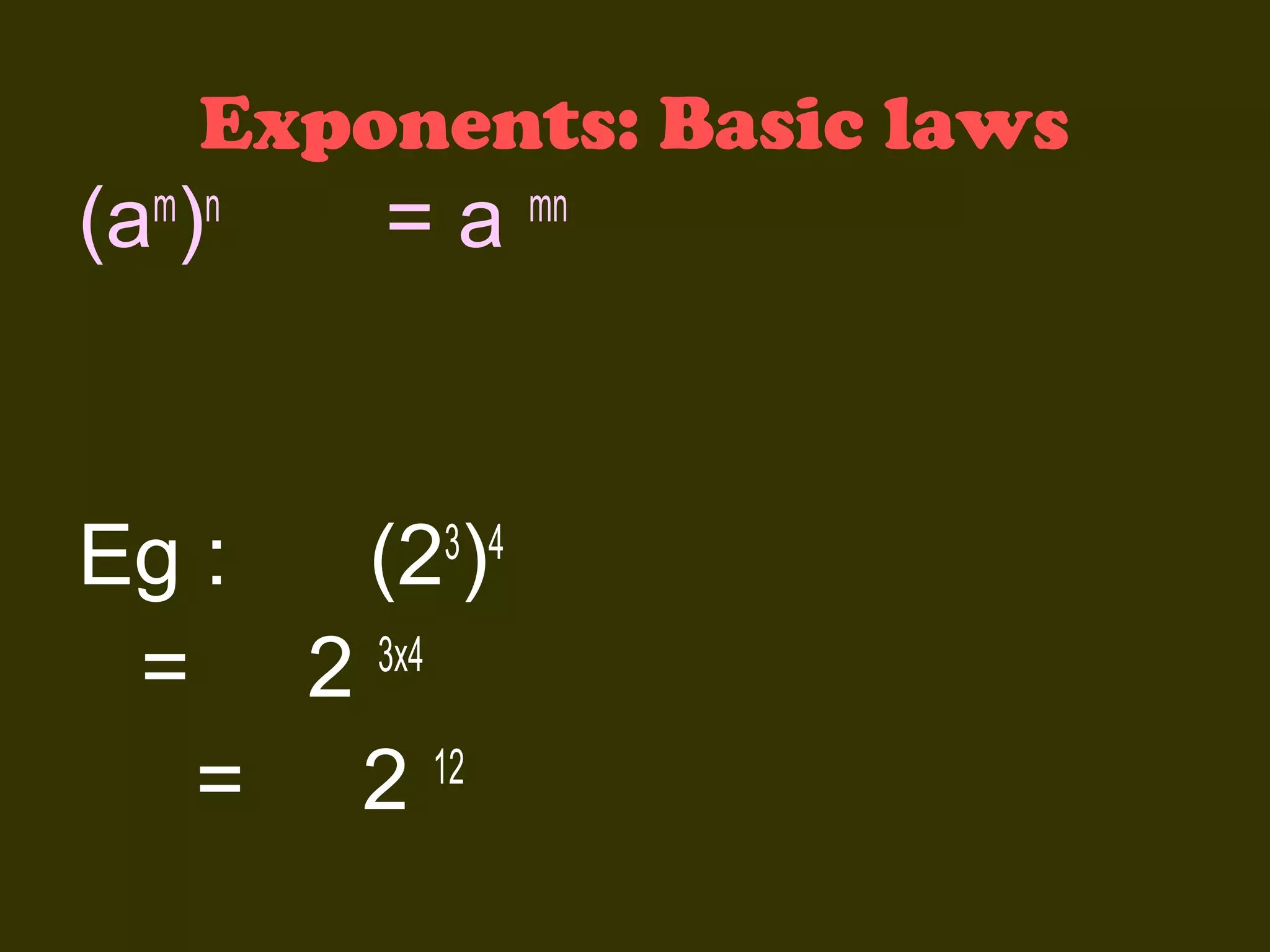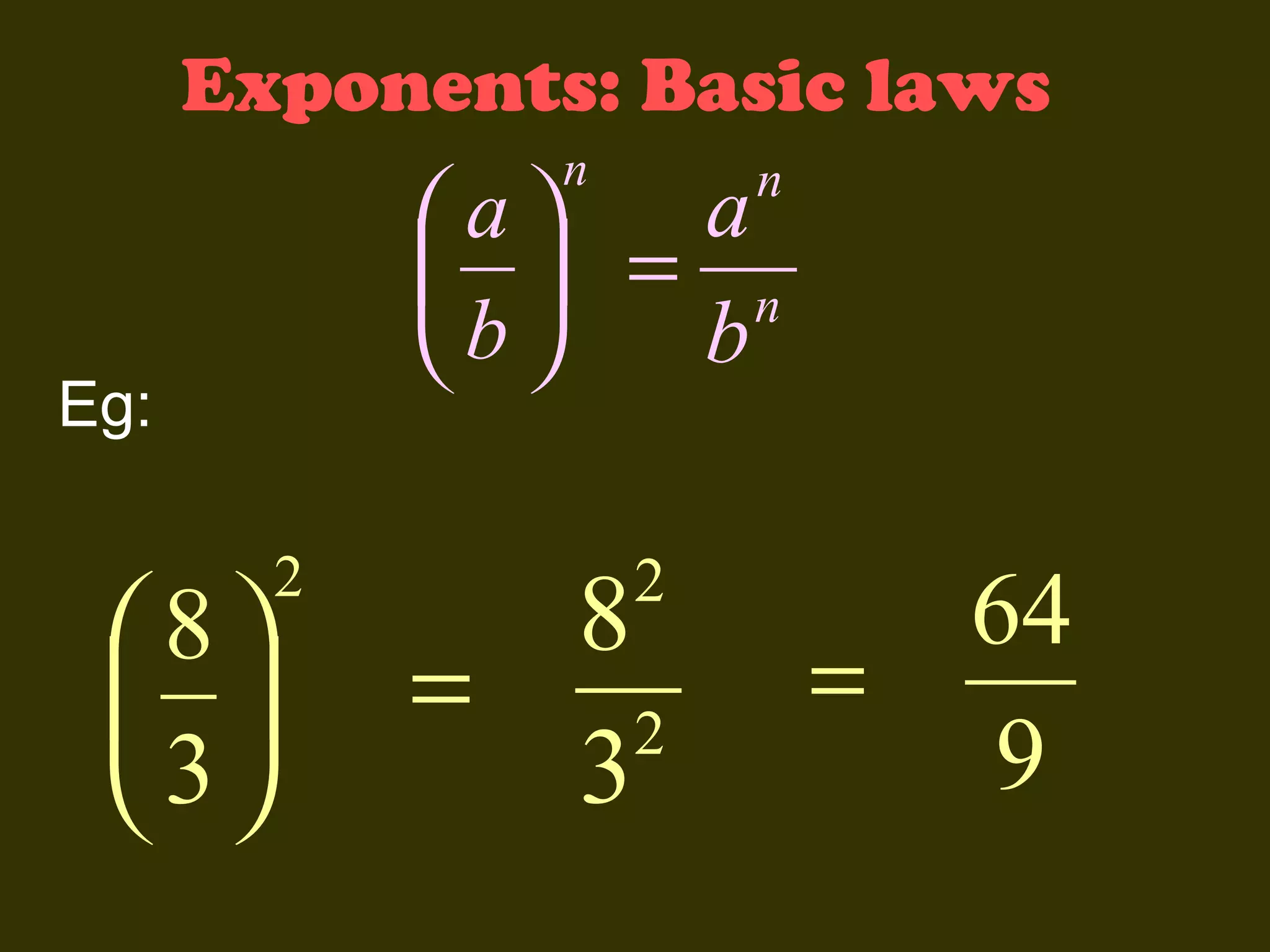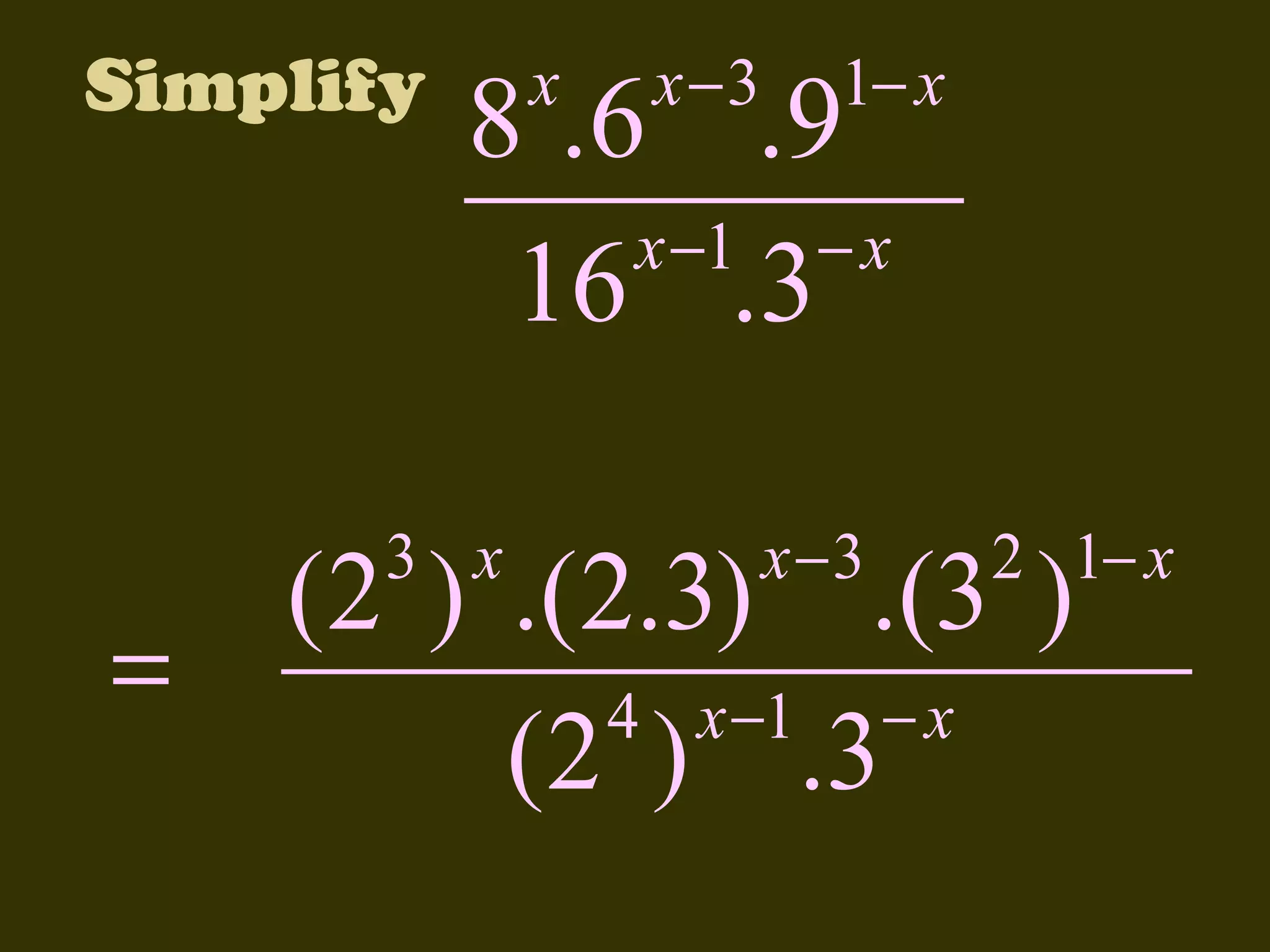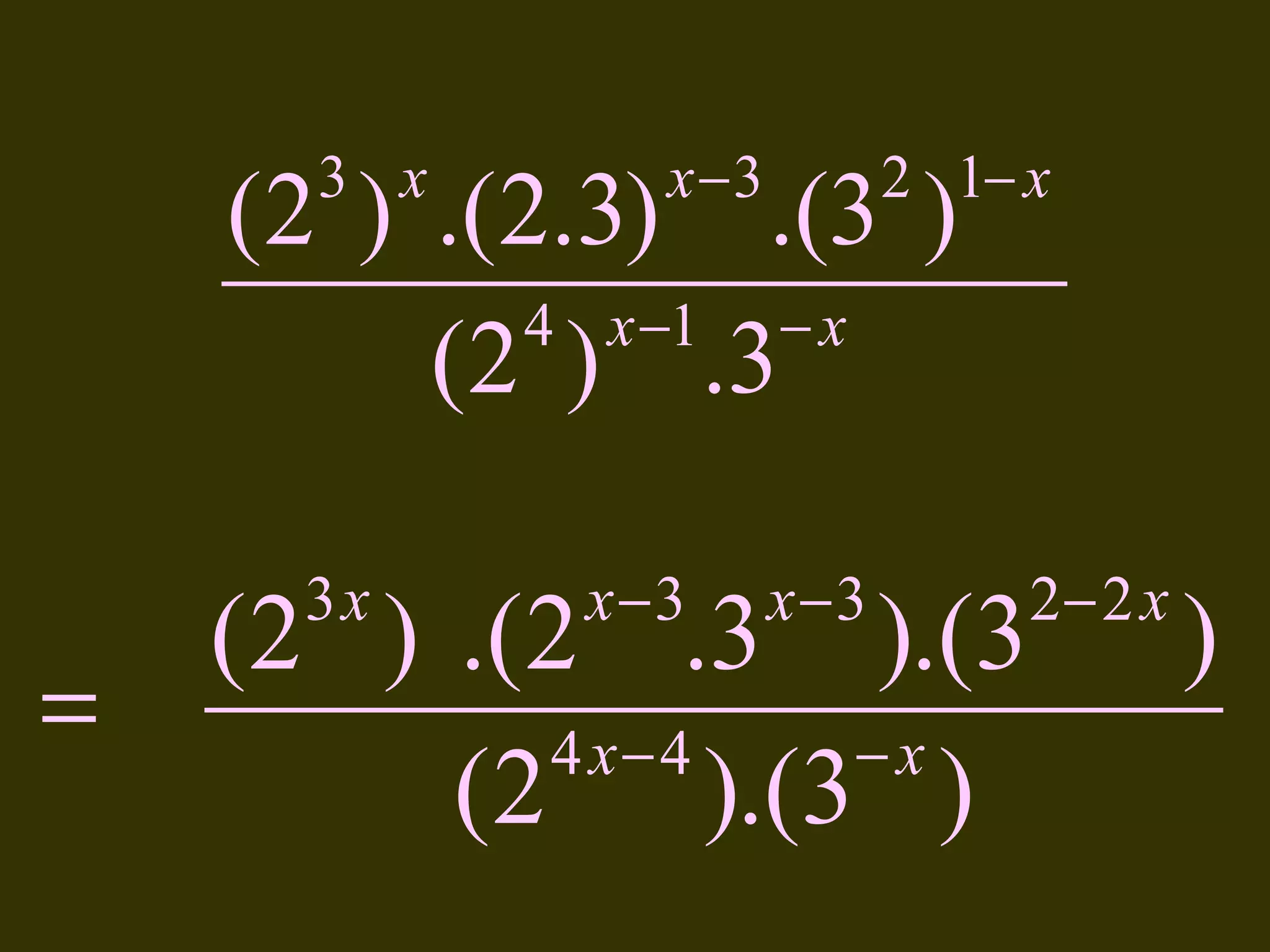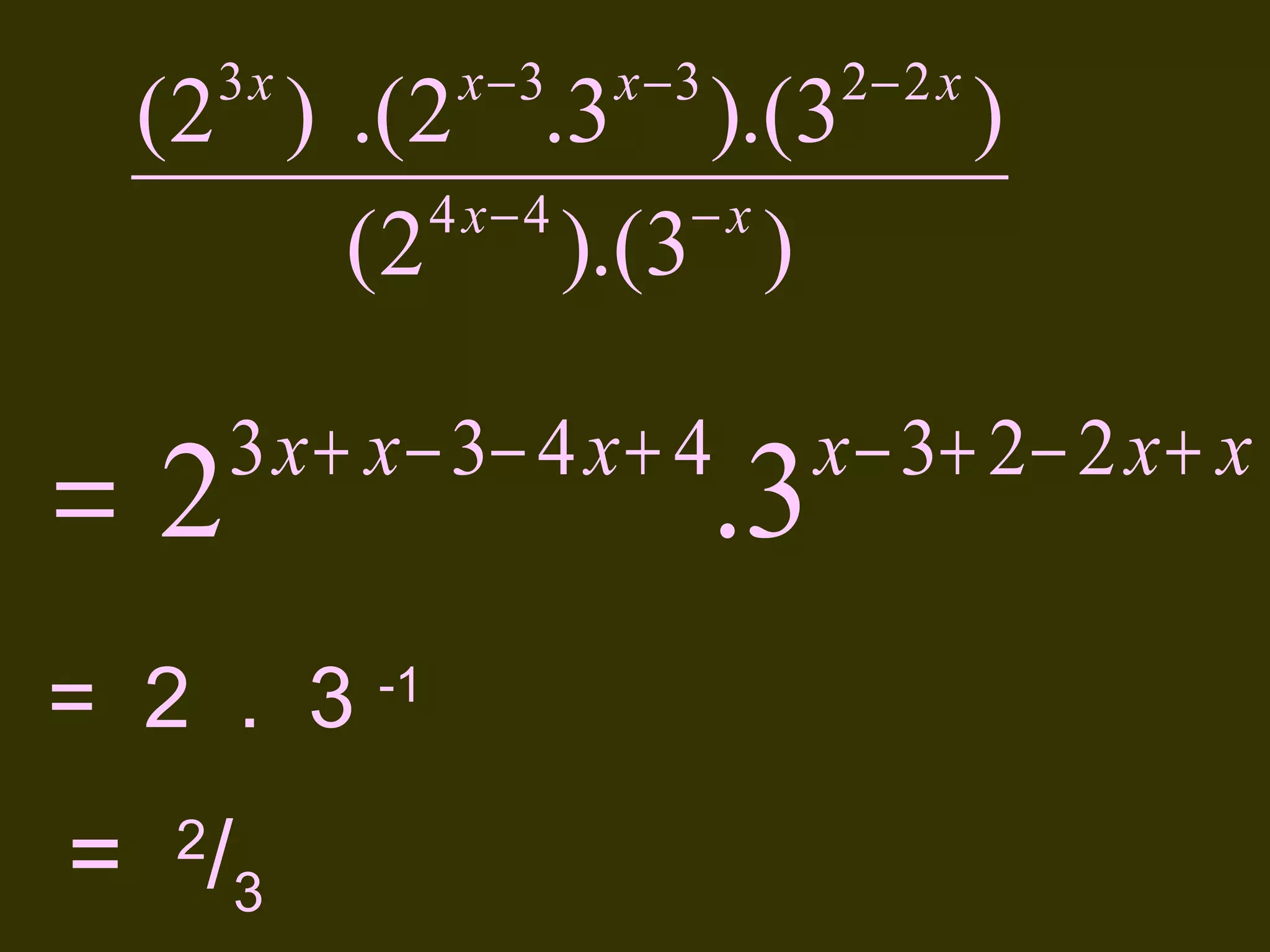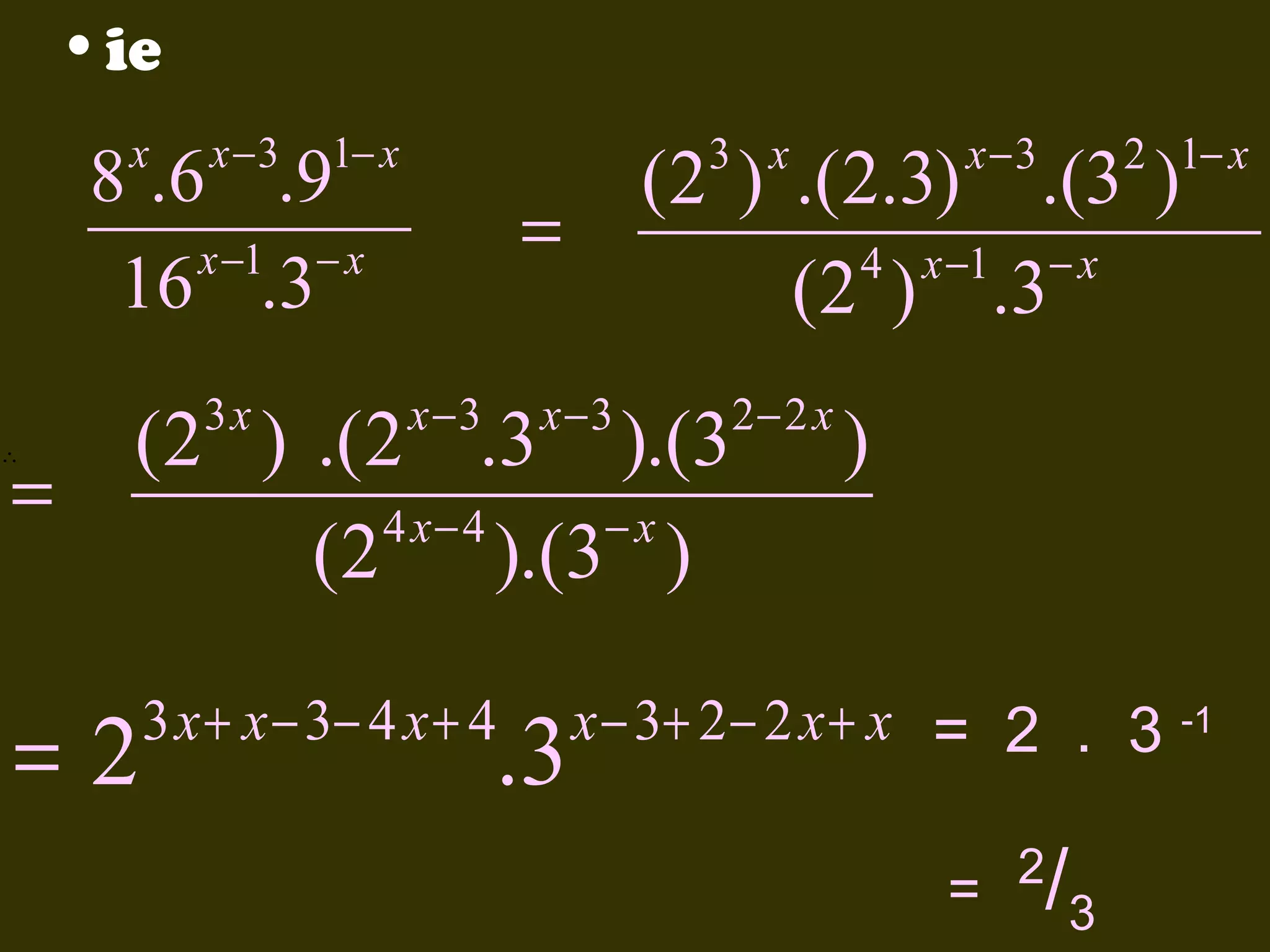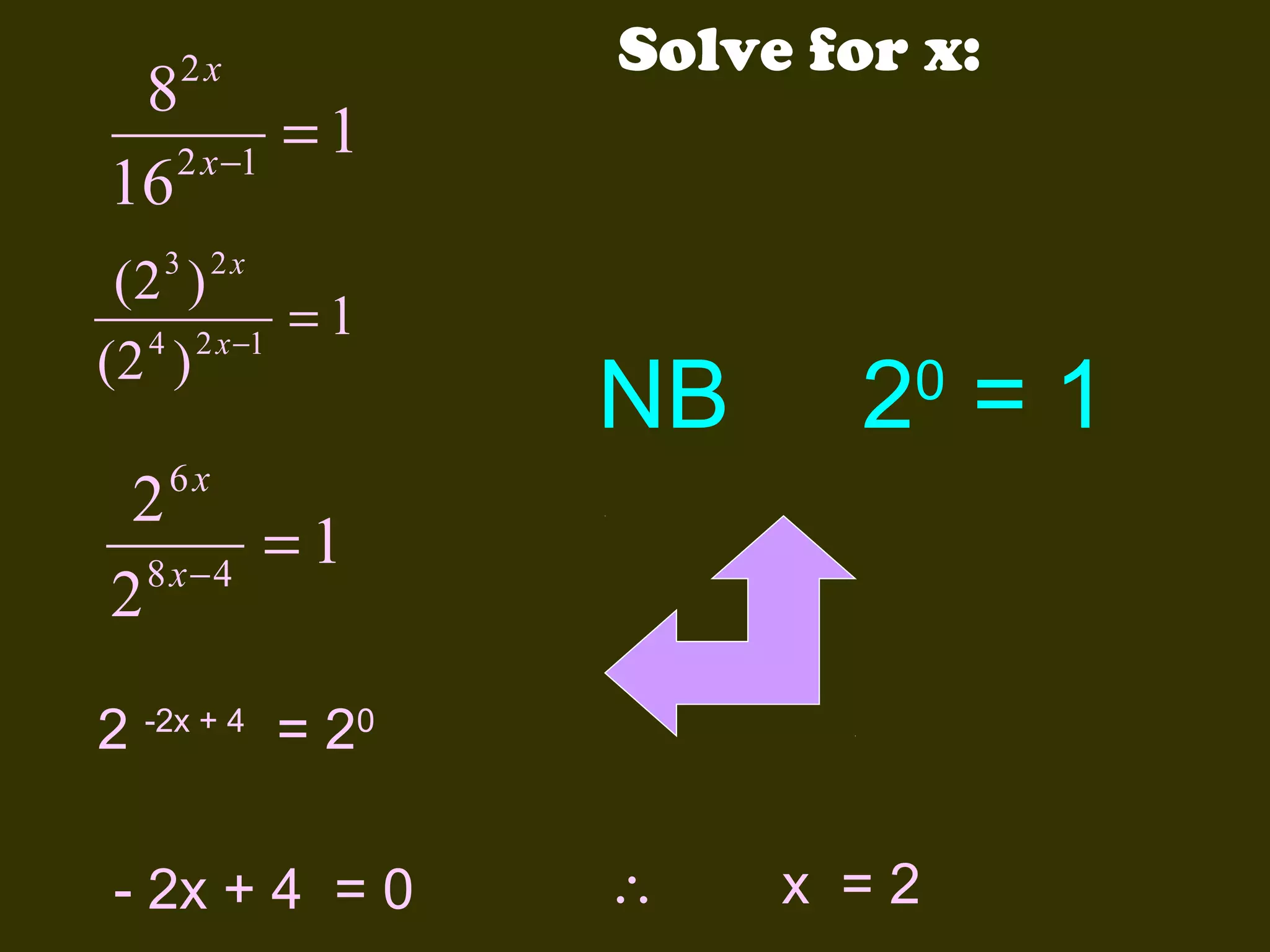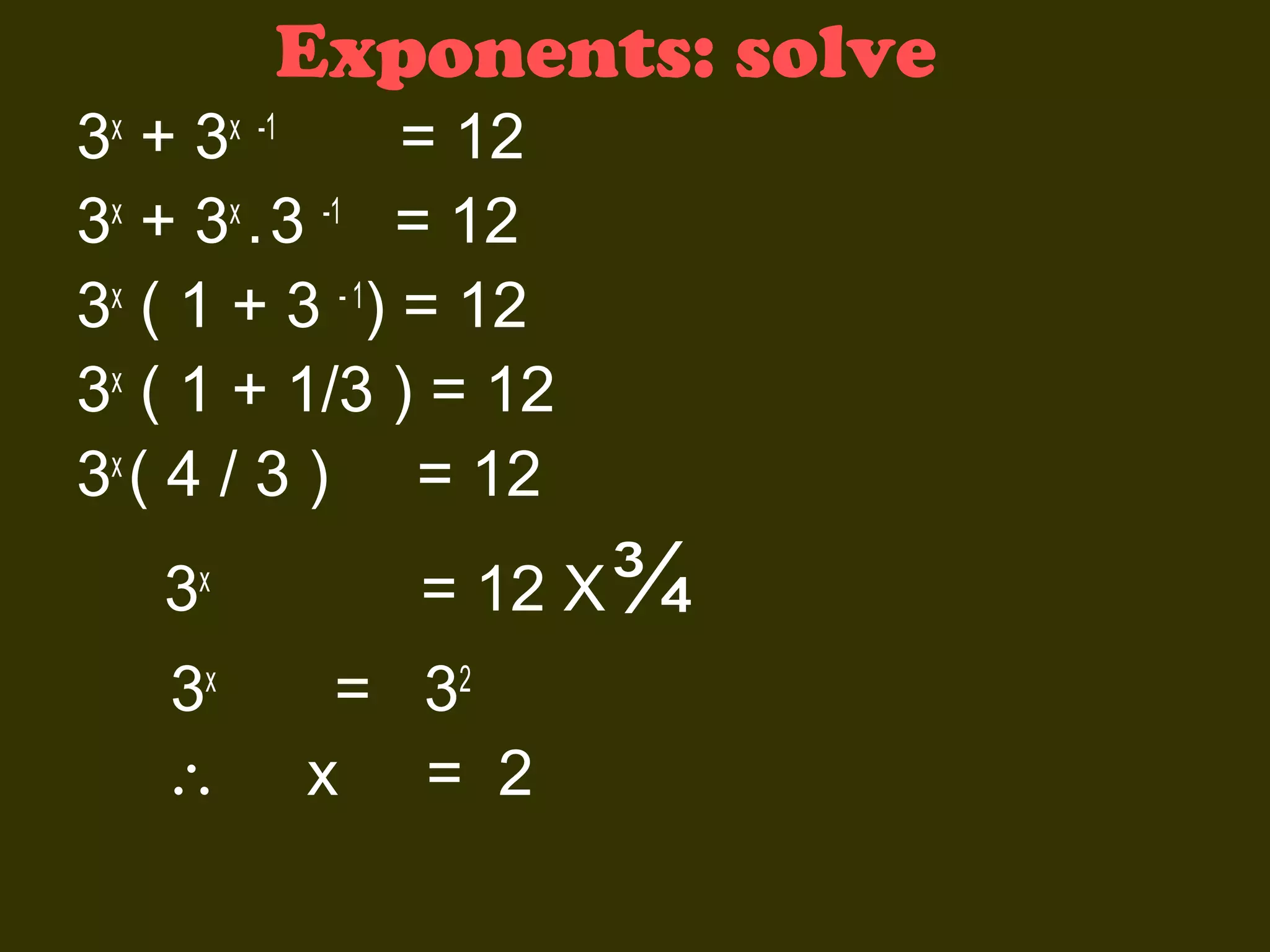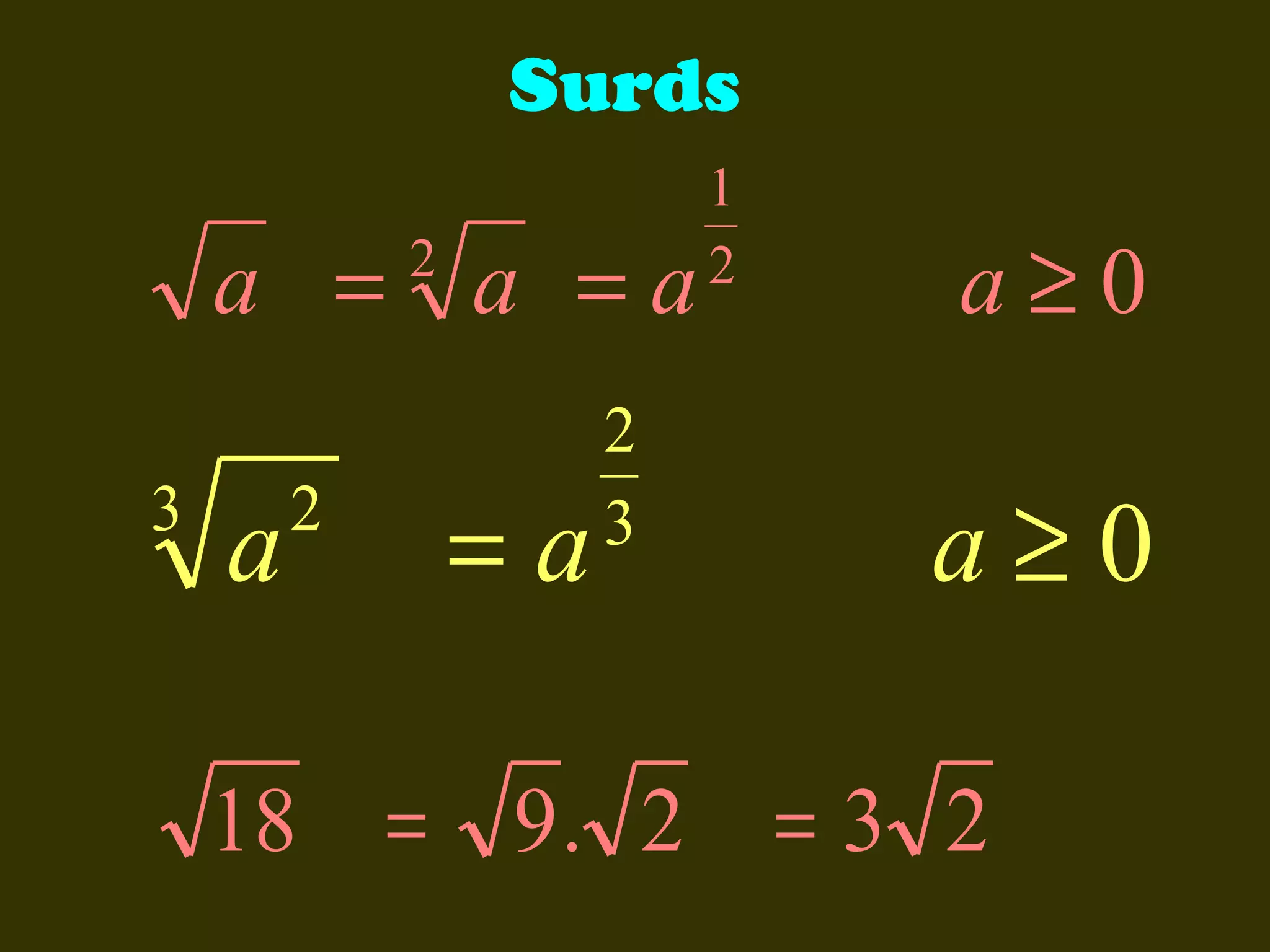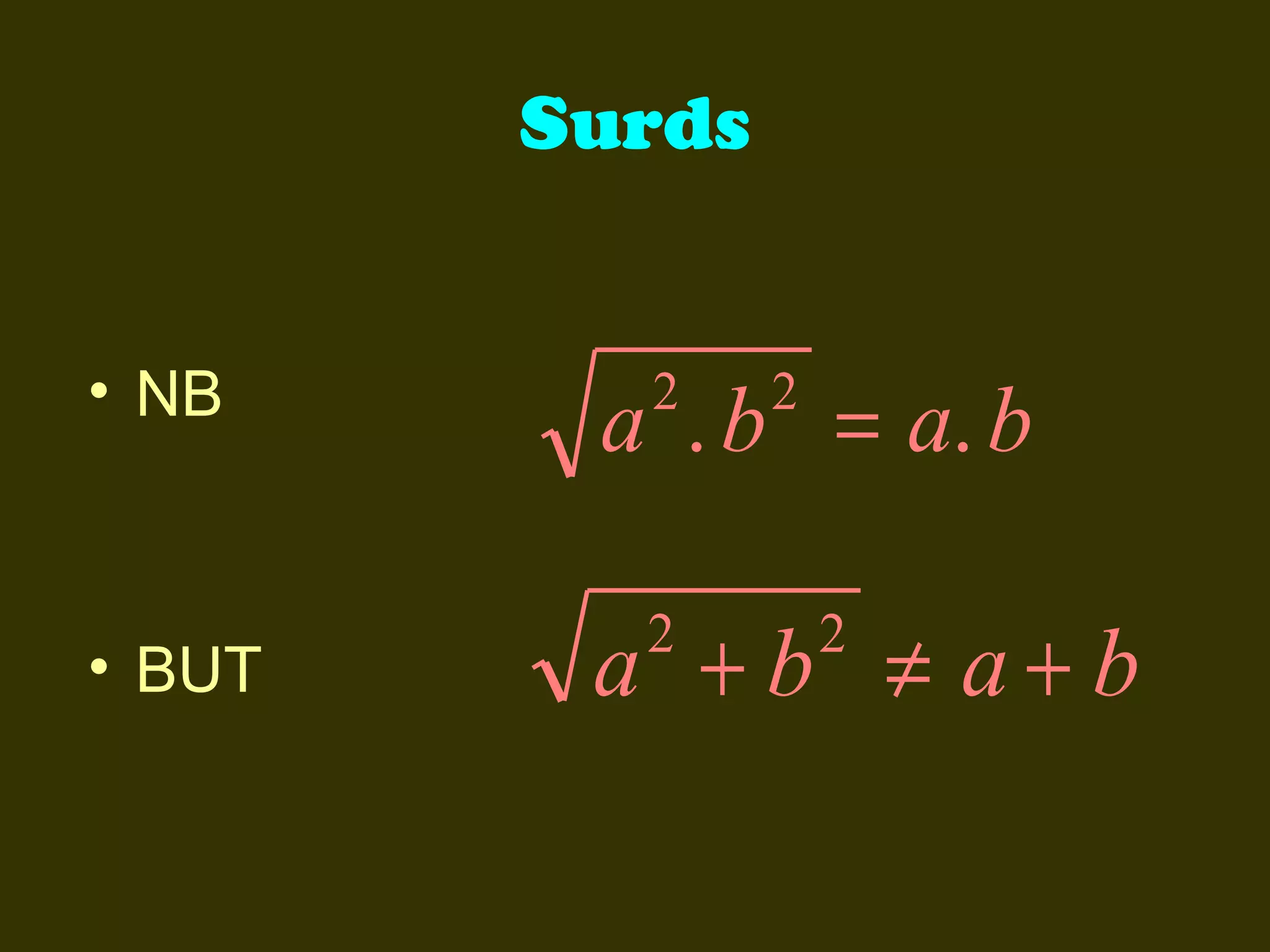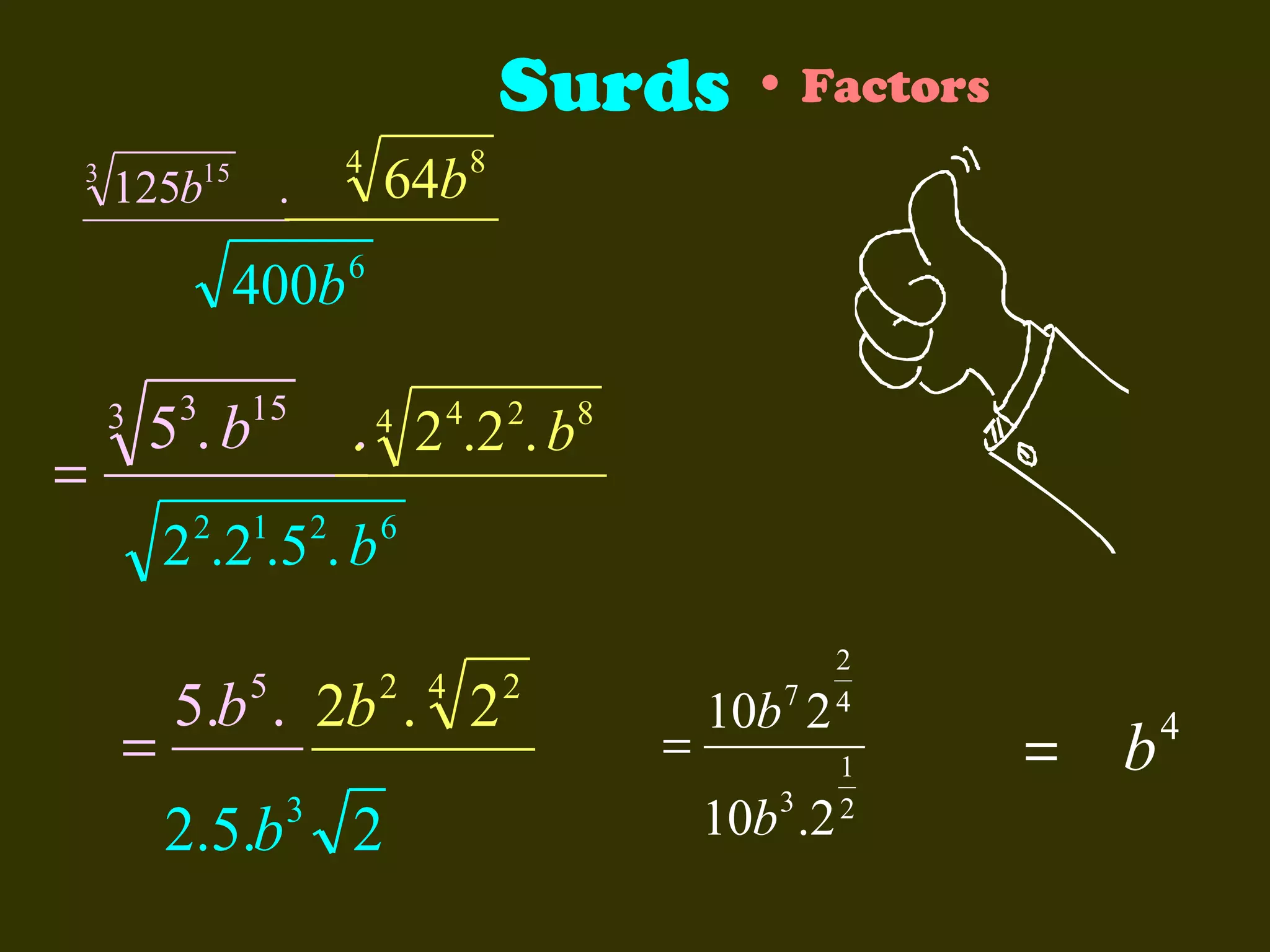This document discusses basic laws and properties of exponents and surds. It begins by defining exponential notation and discussing general cases and special cases of exponents. It then lists several basic laws of exponents, such as am+n = am × an, am/an = am-n, and an-n = a0 = 1. Similar laws are provided for operations involving surds. Examples are provided to illustrate each law. The document also covers simplifying expressions using exponents and surds through factorizing, splitting, and combining like terms. Acknowledgments are provided citing several sources the content was compiled from.

1. Exponents&
Surds
SIBUSISOTHETHWAYO
201219516
BASIC LAWS OF
EXPONENTS

2. Exponential notation

represent as
Base
(real number)
to the th power .
Exponent
Exponent
(integers)
(integers)

3. General case
(n is any positive integers)
Special cases

4. Exponents: Basic laws
a .a
n
= a
m
2 .2
3+2
=2
5
=2
= 32
Eg:
3
m+n
2

5. Exponents: Basic laws
a ÷a
n
Eg :
m
= a
n–m
3 ÷3
= 3 5–3
2
= 3
= 9
5
3

6. Exponents: Basic laws
a
n–n
Eg
=a
4
2
4
2
= 24-4
= 20
=1
0
=1

7. Exponents: Basic laws
(ab)
Eg:
=a .b
n
n
n
62
=( 2.3)
2
= 22. 32
= 4.9
∴ 6 = 36
2

8. Exponents: Basic laws
(a )
m n
=a
Eg :
(23)4
= 2 3x4
= 2 12
mn

9. Exponents: Basic laws
n
a
a
  = n
b
b
Eg:
8
 
3
n
2
2
8
=
2
3
=
64
9

10. Exponents: Basic
NB
• 2a = a + a = 2 x a
• a2 = a . a
• ( a + b)2 = a2 + 2ab + b2 ≠ (a2 +b2)

11. Exponents
an = a . a . a . a ... to n factors
a > 0 and a ≠ 1, n ε N
a n . a m = a m+n
a n ÷ a m = a n–m
an – n
= a0 = 1
(ab)n
= a n . bn
(am)n
= a mn
a
 
b
n
n
a
= n
b

12. Simplify
=
x
x −3
1− x
8 .6 .9
x −1 − x
16 .3
3 x
x−3
2 1− x
(2 ) .(2.3) .(3 )
4 x −1 − x
(2 ) .3

13. 3 x
x−3
2 1− x
(2 ) .(2.3) .(3 )
4 x −1 − x
(2 ) .3
=
3x
x−3
x−3
(2 ) .(2 .3 ).(3
4 x− 4
−x
(2 ).(3 )
2− 2 x
)

14. x −3
3x
x−3
(2 ) .(2 .3 ).(3
4 x− 4
−x
(2 ).(3 )
=2
3 x + x − 3− 4 x + 4
= 2 . 3
= /3
2
.3
-1
2− 2 x
)
x − 3+ 2 − 2 x + x

15. • ie
x
x −3
1− x
8 .6 .9
x −1 − x
16 .3
=
∴
3x
x−3
(2 ) .(2 .3 ).(3
4 x− 4
−x
(2 ).(3 )
=2
3 x + x − 3− 4 x + 4
.3
2 1− x
(2 ) .(2.3) .(3 )
4 x −1 − x
( 2 ) .3
=
x −3
x−3
3 x
2− 2 x
)
x − 3+ 2 − 2 x + x = 2 . 3
= 2 /3
-1

16. 2x
8
=1
2 x −1
16
Solve for x:
3 2x
(2 )
=1
4 2 x −1
(2 )
NB
2 =1
0
6x
2
=1
8 x−4
2
2 -2x + 4 = 20
- 2x + 4 = 0
∴
x =2

17. Exponents: solve
3x + 3x -1
= 12
3x + 3x . 3 -1 = 12
3x ( 1 + 3 - 1) = 12
3x ( 1 + 1/3 ) = 12
3x ( 4 / 3 ) = 12
3x
3x
∴
= 12 X ¾
= 32
x = 2

18. Surds & Exponents
example
Basic Laws

19. Surds
a = a =a
2
3
a
2
=a
2
3
1
2
a≥0
a≥0
18 = 9 . 2 = 3 2

20. Surds
• NB
a . b = a. b
• BUT
a +b ≠ a+b
2
2
2
2

21. Surds • Factors
3
15
125b
4
.
400b
=
3
3
15
5 .b
2
1
6
. 4 2 4.2 2. b8
2
2 .2 . 5 . b
=
5
64b
8
6
2 4
5.b . 2b . 2
2.5.b
3
2
2
=
7
10b 2
10b 3 .2
2
4
1
2
= b
4

22. Surds
Simplify: Terms
Pure surds
Factorise into
perfect
squares
Split
Simplify
50 −
18
= 25.2 − 9.2
= 25. 2 − 9 . 2
=5 2 − 3 2
=2 2

23. REFERENCE-LIST
• This power point presentation is the
combination of five power piont
presentations, which I gathered on
my slide share. However, here below
on the next slide are the auther’s I
used on my presentation.

24. Thank you Guys
Acknowledgments
to
 Nurul Atiyah binti Ripin
 Irma Naziela binti Rosli
 Stephen Corcoran
 Genny Simpson
 http://www.slideshare.net/sibusisot
/savedfiles?s_title=exponent-rules-