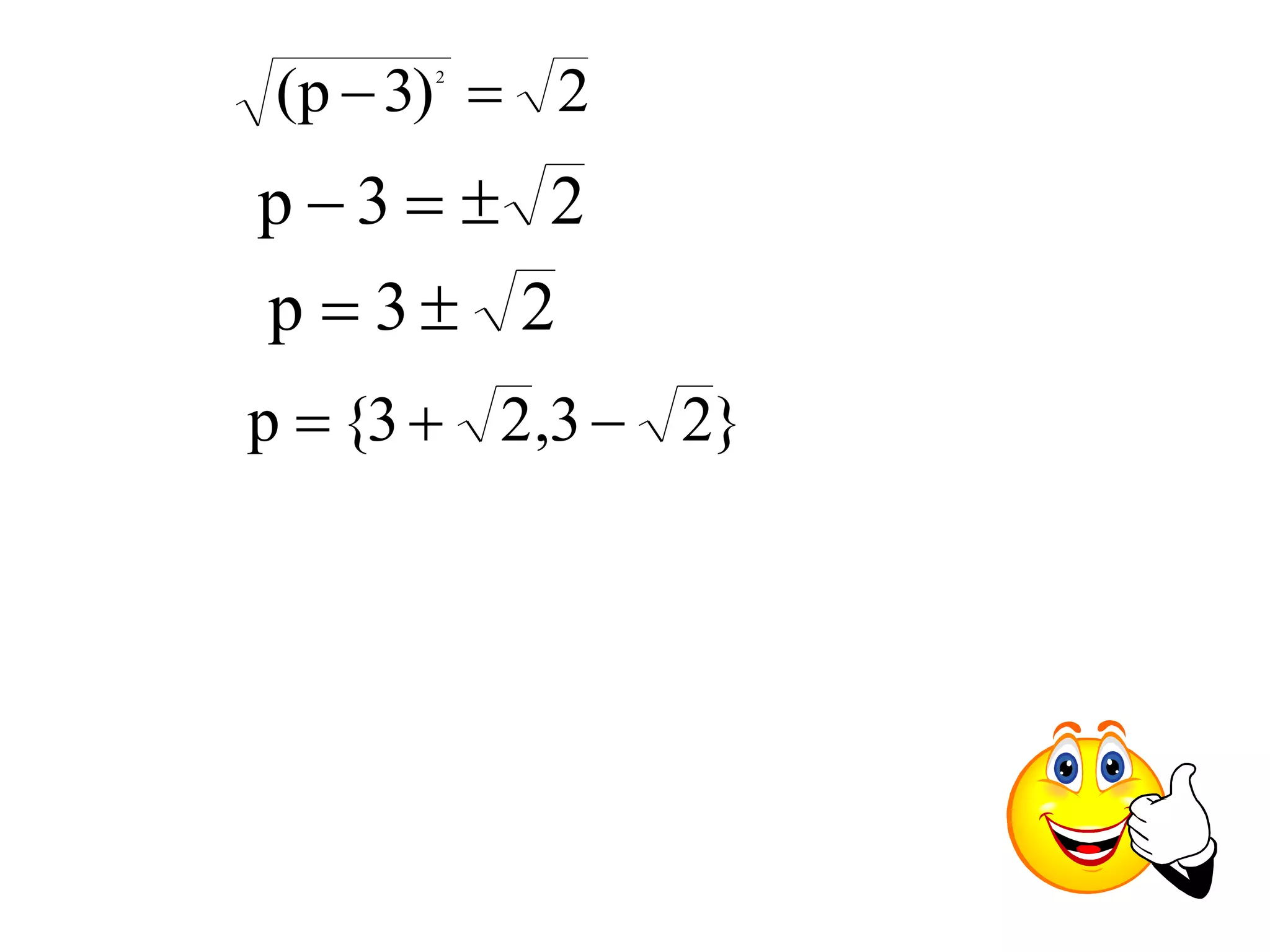This document provides an overview of solving quadratic equations through various methods, including factoring, using the zero product property, completing the square, and using the quadratic formula. Key points covered include: - A quadratic equation is of the form ax2 + bx + c = 0. - Quadratic equations can be solved by factoring the left side into two binomial factors and setting each equal to 0. - The quadratic formula, x = (-b ± √(b2 - 4ac))/2a, can be derived from completing the square and used to solve any quadratic equation. - Examples are provided to demonstrate solving quadratic equations through factoring, completing the square, and using the quadratic formula.

1. QUADRATIC
EQUATIONS
MSJC ~ San Jacinto Campus
Math Center Workshop Series
Janice Levasseur

2. Basics
• A quadratic equation is an equation
equivalent to an equation of the type
ax2 + bx + c = 0, where a is nonzero
• We can solve a quadratic equation by
factoring and using The Principle of Zero
Products
If ab = 0, then either a = 0, b = 0, or both a
and b = 0.

3. Ex: Solve (4t + 1)(3t – 5) = 0
Notice the equation as given is of the form ab = 0
 set each factor equal to 0 and solve
4t + 1 = 0 Subtract 1
4t = – 1 Divide by 4
t = – ¼
3t – 5 = 0 Add 5
3t = 5 Divide by 3
t = 5/3
Solution: t = - ¼ and 5/3  t = {- ¼, 5/3}

4. Ex: Solve x2 + 7x + 6 = 0
Quadratic equation  factor the left hand side (LHS)
x2 + 7x + 6 = (x + 6 )(x + 1 )
 x2 + 7x + 6 = (x + 6)(x + 1) = 0
Now the equation as given is of the form ab = 0
 set each factor equal to 0 and solve
x + 6 = 0
x = – 6
x + 1 = 0
x = – 1
Solution: x = - 6 and – 1  x = {-6, -1}

5. Ex: Solve x2 + 10x = – 25
Quadratic equation but not of the form ax2 + bx + c = 0
Add 25  x2 + 10x + 25 = 0
Quadratic equation  factor the left hand side (LHS)
x2 + 10x + 25 = (x + 5 )(x + 5 )
 x2 + 10x + 25 = (x + 5)(x + 5) = 0
Now the equation as given is of the form ab = 0
 set each factor equal to 0 and solve
x + 5 = 0
x = – 5
x + 5 = 0
x = – 5
Solution: x = - 5  x = {- 5}  repeated root

6. Ex: Solve 12y2 – 5y = 2
Quadratic equation but not of the form ax2 + bx + c = 0
Subtract 2  12y2 – 5y – 2 = 0
Quadratic equation  factor the left hand side (LHS)
ac method  a = 12 and c = – 2
ac = (12)(-2) = - 24  factors of – 24 that sum to - 5
1&-24, 2&-12, 3&-8, . . . 
 12y2 – 5y – 2 = 12y2 + 3y – 8y – 2
= 3y(4y + 1) – 2(4y + 1)
= (3y – 2)(4y + 1)

7.  12y2 – 5y – 2 = 0
 12y2 – 5y – 2 = (3y - 2)(4y + 1) = 0
Now the equation as given is of the form ab = 0
 set each factor equal to 0 and solve
3y – 2 = 0
3y = 2
4y + 1 = 0
4y = – 1
y = 2/3 y = – ¼
Solution: y = 2/3 and – ¼  y = {2/3, - ¼ }

8. Ex: Solve 5x2 = 6x
Quadratic equation but not of the form ax2 + bx + c = 0
Subtract 6x  5x2 – 6x = 0
Quadratic equation  factor the left hand side (LHS)
5x2 – 6x = x( 5 x – 6 )
 5x2 – 6x = x(5x – 6) = 0
Now the equation as given is of the form ab = 0
 set each factor equal to 0 and solve
x = 0
5x – 6 = 0
5x = 6
x = 6/5
Solution: x = 0 and 6/5  x = {0, 6/5}

9. Solving by taking square roots
• An alternate method of solving a quadratic
equation is using the Principle of Taking
the Square Root of Each Side of an
Equation
If x2 = a, then x = + a

10. Ex: Solve by taking square roots 3x2 – 36 = 0
First, isolate x2: 3x2 – 36 = 0
3x2 = 36
x2 = 12
Now take the square root of both sides:
x 12 2 
x   12
x   2  2  3
x   2 3

11. Ex: Solve by taking square roots 4(z – 3)2 = 100
First, isolate the squared factor:
4(z – 3)2 = 100
(z – 3)2 = 25
Now take the square root of both sides:
(z 3) 25 2  
z  3   25
z – 3 = + 5
z = 3 + 5
 z = 3 + 5 = 8 and z = 3 – 5 = – 2

12. Ex: Solve by taking square roots 5(x + 5)2 – 75 = 0
First, isolate the squared factor:
5(x + 5)2 = 75
(x + 5)2 = 15
Now take the square root of both sides:
( x  5 )2  15
x  5   15
x  5  15
x  5  15 , x  5  15

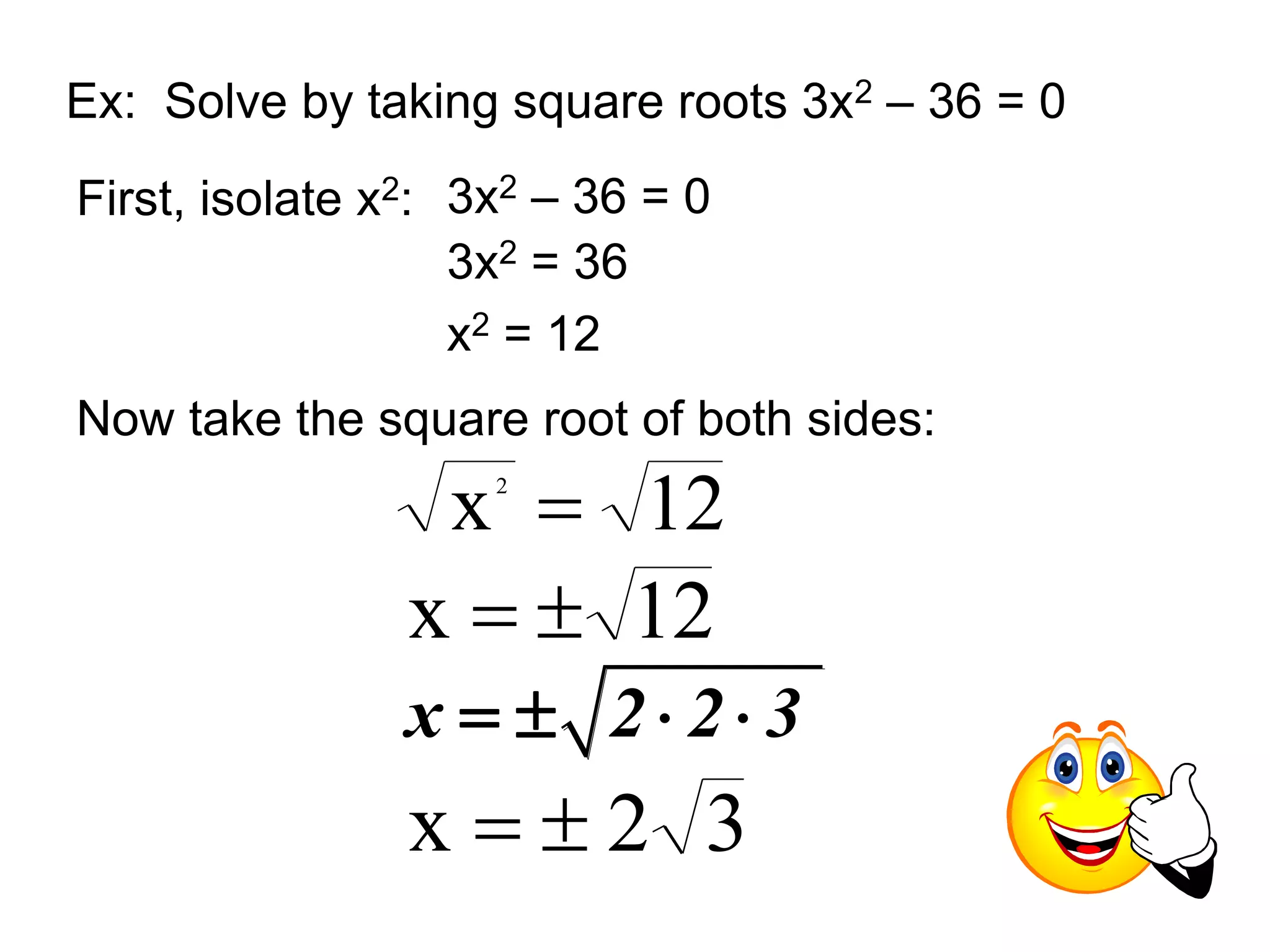
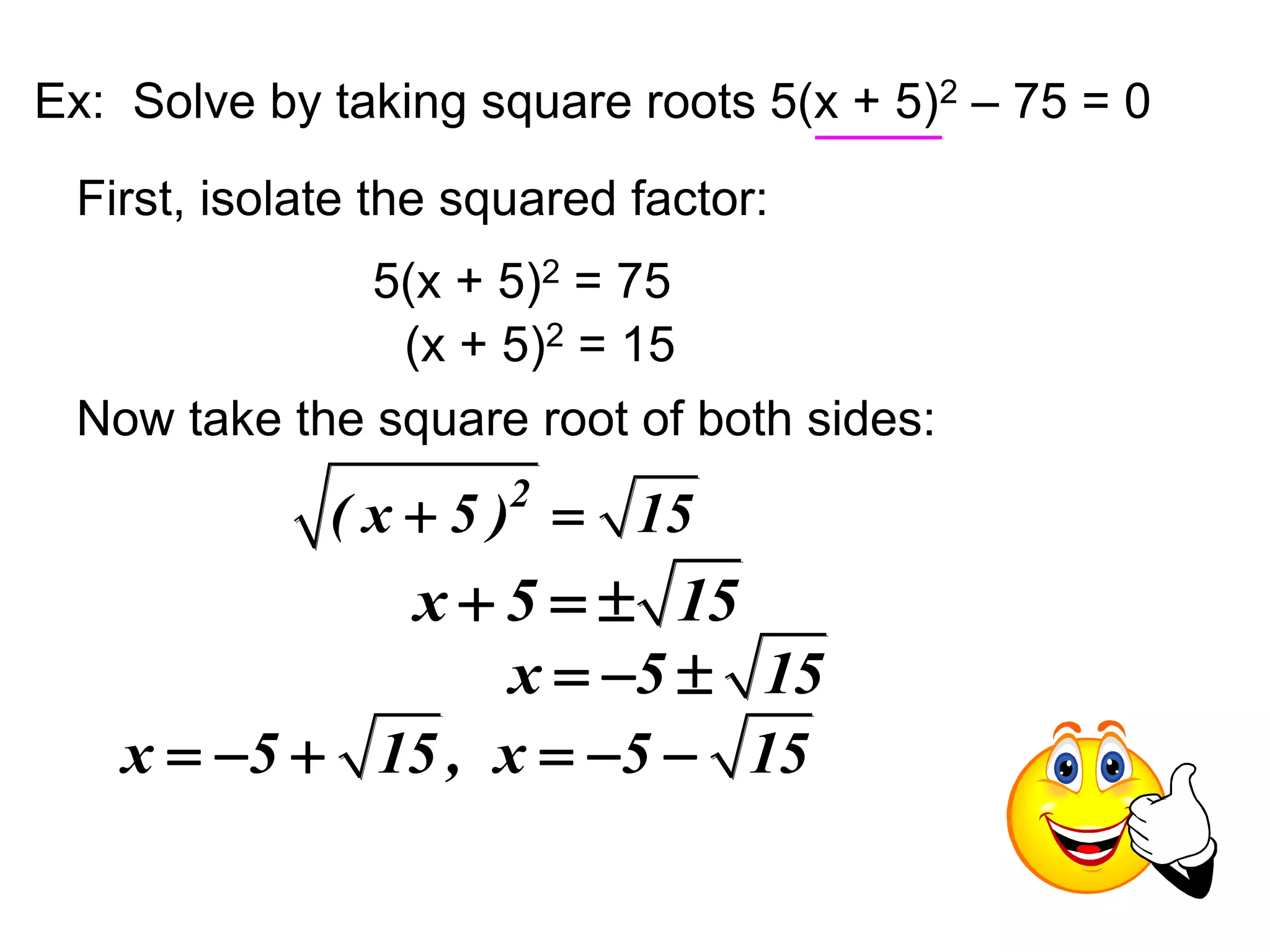
13. Completing the Square
• Recall from factoring that a Perfect-Square
Trinomial is the square of a binomial:
Perfect square Trinomial Binomial Square
x2 + 8x + 16 (x + 4)2
x2 – 6x + 9 (x – 3)2
• The square of half of the coefficient of x
equals the constant term:
( ½ * 8 )2 = 16
[½ (-6)]2 = 9

14. Completing the Square
• Write the equation in the form x2 + bx = c
• Add to each side of the equation [½(b)]2
• Factor the perfect-square trinomial
x2 + bx + [½(b)] 2 = c + [½(b)]2
• Take the square root of both sides of the
equation
• Solve for x

15. Ex: Solve w2 + 6w + 4 = 0 by completing the square
First, rewrite the equation with the constant on one
side of the equals and a lead coefficient of 1.
w2 + 6
6w = – 4
Add [½(b)]2 to both sides: b =
6  [½(6)]2 = 32 = 9
w2 + 6w + 9 = – 4 + 9
w2 + 6w + 9 = 5
(w + 3)2 = 5
Now take the square root of both sides

16. 5 ) 3 w ( 2  
w  3   5
w  3 5
w  {3  5,3  5}

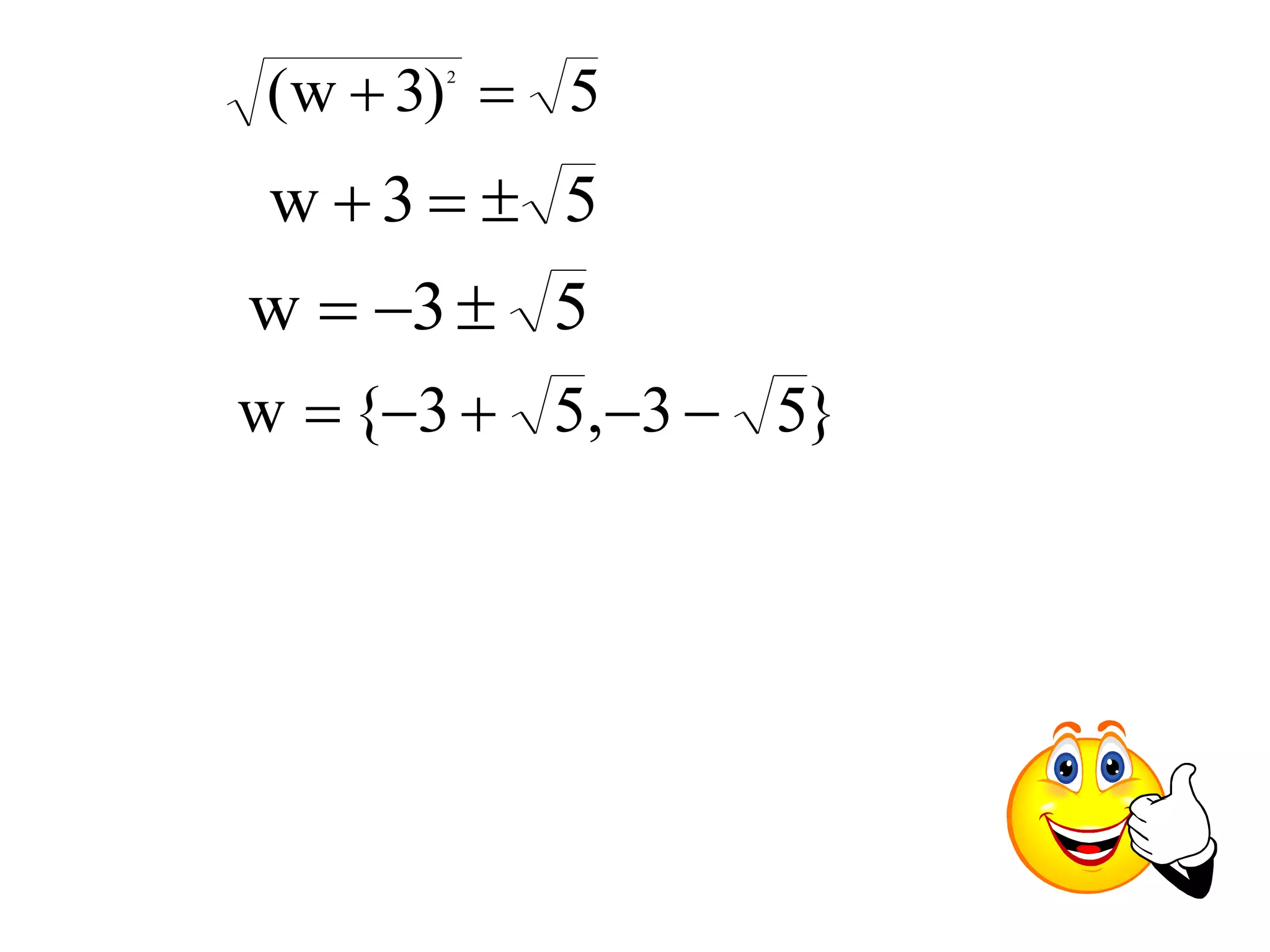
17. Ex: Solve 2r2 = 3 – 5r by completing the square
First, rewrite the equation with the constant on one
side of the equals and a lead coefficient of 1.
2r2 + 5r = 3
 r2 + (5/2)
r = (3/2)
Add [½(b)]2 to both sides: b =
5/2 [½(5/2)]2 = (5/4)2
= 25/16
r2 + (5/2)r + 25/16 = (3/2) + 25/16
r2 + (5/2)r + 25/16 = 24/16 + 25/16
(r + 5/4)2 = 49/16
Now take the square root of both sides

18. (r 5/ 4) 49/16 2  
r  5/ 4  (7/ 4)
r  (5/ 4)  (7/ 4)
r = - (5/4) + (7/4) = 2/4 = ½
and r = - (5/4) - (7/4) = -12/4 = - 3
r = { ½ , - 3}

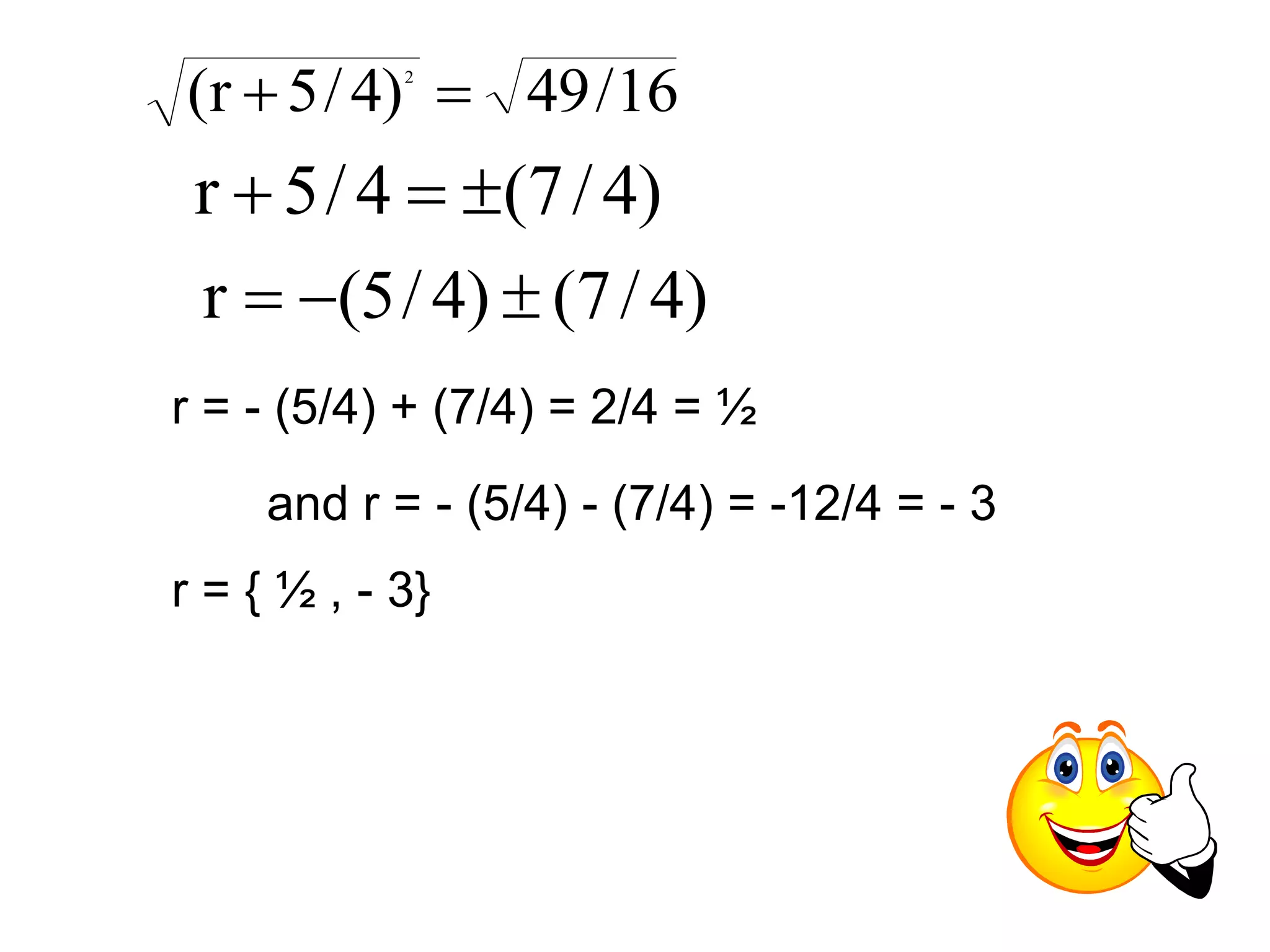
19. Ex: Solve 3p – 5 = (p – 1)(p – 2)
Is this a quadratic equation? FOIL the RHS
3p – 5 = p2 – 2p – p + 2
3p – 5 = p2 – 3p + 2
p2 – 6p + 7 = 0
Collect all terms
A-ha . . .
Quadratic Equation  complete the square
p2 – 6p = – 7  [½(-6)]2 = (-3)2 = 9
p2 – 6p + 9 = – 7 + 9
(p – 3)2 = 2

20. 2 ) 3 p( 2  
p  3   2
p  3  2
p  {3  2,3  2}

21. The Quadratic Formula
• Consider a quadratic equation of the form
ax2 + bx + c = 0 for a nonzero
• Completing the square
ax2  bx   c

b c
x 2  x

a a
b b c b
2 2
2
    
2 2
x x
a 4a a 4a

22. The Quadratic Formula
b b 4ac b
2 2
    
2
  
   
 
b b 2
4ac
2
x
2a 4a
Solutions to ax2 + bx + c = 0 for a nonzero
are
  

2 b b 4ac
x
2a
2
2 2 2
x x
a 4a 4a 4a

23. Ex: Use the Quadratic Formula to solve x2 + 7x + 6
= 0
Recall: For quadratic equation ax2 + bx + c = 0,
the solutions to a quadratic equation are given by
b b 4ac
2a
x
2   

Identify a, b, and c in ax2 + bx + c = 0:
a = 1 b = c =
1
7
7
6
Now evaluate the quadratic formula at the identified
values of a, b, and c

24. 7 7 4(1)(6)
2(1)
x
2   

7 49 24
2
x
  

7 25
2
x
 

7 5
2
x
 

x = ( - 7 + 5)/2 = - 1 and x = (-7 – 5)/2 = - 6
x = { - 1, - 6 }

25. Ex: Use the Quadratic Formula to solve
1
2m2 + m = 0
2
Recall: For quadratic equation ax2 + bx + c = 0,
the solutions to a quadratic equation are given by
4 2   

b b ac
a
m
2
Identify a, b, and c in am2 + bm + c = 0:
a = 2 b = 1
c =
- 10
– 10
Now evaluate the quadratic formula at the identified
values of a, b, and c

26. 1 1 4(2)( 10)
2(2)
m
2    

1 1 80
4
m
  

1 81
4
m
 

1 9
4
m
 

m = ( - 1 + 9)/4 = 2 and m = (-1 – 9)/4 = - 5/2
m = { 2, - 5/2 }

27. Any questions . . .