Exponents and powers are perhaps the most fundamental concepts found in mathematics, which has made it easy to get the same number multiplied times over again. An exponent is how many times that number, known as a base, is multiplied to itself. For instance, in (2^3), the number 2 is the base, and the exponent (power) being 3 shows that this number, 2 is multiplied by itself three times (same base) i.e. (2 times 2 times 2 =8). The result obtained from such multiplication is power. The result obtained from such multiplication is referred to as the power. These concepts are vital in understanding the difference between exponential and power functions and their applications in mathematics, from basic arithmetic to advanced algebra and scientific calculations. Mastering the rules of exponents and powers is crucial for solving equations, simplifying expressions, and efficiently addressing real-world problems. This ensures that calculations are devised and executed streamlined and simplified. Exponents and powers are mathematical tools that make writing and calculating repeated multiplication of the same number easy. Let's break it down step by step to better understand powers and exponents with important rules An exponent is the number written above and to the right of another number. It tells us how many times the base number is multiplied by itself. The exponent tells how many times a number is multiplied by its power. For example, (2^3) (read as two raised to the power of 3) means (2 times 2 times 2 = 8). Here, 3 is the exponent of a number. 2 is the base (the number being multiplied). 3 is the exponent (the number of times 2 is multiplied by itself).

1. What are Exponents and
Powers? Definitions, Rules, and
Examples
Exponents and powers are perhaps the most fundamental concepts found
in mathematics, which has made it easy to get the same number multiplied
times over again. An exponent is how many times that number, known as a
base, is multiplied to itself. For instance, in (2^3), the number 2 is the base,
and the exponent (power) being 3 shows that this number, 2 is multiplied
by itself three times (same base) i.e. (2 times 2 times 2 =8). The result
obtained from such multiplication is power. The result obtained from such
multiplication is referred to as the power. These concepts are vital in
understanding the difference between exponential and power functions
and their applications in mathematics, from basic arithmetic to advanced

2. algebra and scientific calculations. Mastering the rules of exponents and
powers is crucial for solving equations, simplifying expressions, and
efficiently addressing real-world problems. This ensures that calculations
are devised and executed streamlined and simplified.
Exponents and powers are mathematical tools that make writing and
calculating repeated multiplication of the same number easy.
Let's break it down step by step to better understand powers and
exponents with important rules.
What is an Exponent and Power?

4. An exponent is the number written above and to the right of another
number. It tells us how many times the base number is multiplied by itself.
The exponent tells how many times a number is multiplied by its power.
For example, (2^3) (read as two raised to the power of 3) means (2 times 2
times 2 = 8).​
Here, 3 is the exponent of a number.
●​ 2 is the base (the number being multiplied).
●​ 3 is the exponent (the number of times 2 is multiplied by itself).
A power is defined as the result of using an exponent.
For example, In (2^3 = 8), the number 8 is the power. The power rule is the
base number raised to the power 3.

5. So, when we write (3^4), it means 3 times 3 times 3 times 3 equal 81
Here, 81 is the power. Therefore, it represents repeated multiplication.
Rules of Exponents

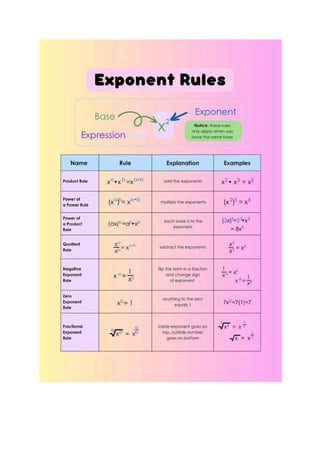
7. Understanding the rules of exponents enables us to work with them easily.
Here are some of the most important ones:
1.​ Multiplying Powers with the Same Base: When multiplying numbers
with the same base, add the exponents. a^m times a^n = a^{m+n}​
Example: (2^3 times 2^2 = 2^{3+2} = 2^5 = 32).
2.​ Dividing Powers with the Same Base: When dividing numbers with
the same base, subtract the exponents. a^m div a^n = a^{m-n}​
Example: (5^4 div 5^2 = 5^{4-2} = 5^2 = 25).
3.​ Power of a Power Rule:​
When raising a power to another power, multiply the exponents.​
[​
(a^m)^n = a^{m times n}​
]​
Example: ((3^2)^3 = 3^{2 times 3} = 3^6 = 729).
4.​ Zero Exponent Rule:​
Any number raised to the power of 0 is always 1 (except 0 itself).​
[a^0 = 1]​
Example: (4^0 = 1).
5.​ Negative Exponent Rule: The negative exponent means the
reciprocal (or the "flipped" version) of the base raised to the positive
exponent.​

8. [ a^{-n} = frac{1}{a^n}]​
Example: (2^{-3} =frac{1}{2^3} = frac{1}{8}).
Why Are Exponents and Powers Useful?
Exponents and powers help us compactly express large or small numbers.
For example:​
- The large number 1,000,000 can be written as (10^6).​
- The tiny number 0.00001 can be written as (10^{-5}).
Exponents and powers are also used in sciences to calculate growth, in
computing to measure speed or storage, and in geometry to calculate area
and volume.
What Is an Exponent and Power?

9. An exponent of a number shows how many times a number, called the
base, is multiplied by itself. When we use exponents, we write a small given
number above and to the right of the base. This small positive number is
called the exponent.
Example:​
2^3 = 2 · 2 ·2 = 8 (mathematical expression)
2 is the base.
3 is the exponent- it tells us how many times to multiply the base by itself.
(third power)
8 is the value-the result of multiplication. (number expressed after the
second power of rule)

10. Real-Life Examples
Following are the real-life situations which involve exponents and power
exponents exponent.
Doubling Bacteria Growth
Imagine one bacterium doubles every hour. By the end of 3 hours, the
cumulative total number of bacteria is:
Expression: [2^3 = 2 times 2 times 2 = 8]​
Such exponents make the multiple growths easily computable.
It can also be used to ascertain the pH scale.

11. Square Area
In finding the area of a square with a side length of 4, we multiply the side
by itself:
[4^2 = 4 times 4 = 16]
Large Numbers in Science
In astronomy, the distance from Earth to the Sun is roughly (1.5 times 10^8)
kilometres. That's a lot more concise than 150,000,000 kilometres.
Why Does It Matter To Know Exponents and Powers?

12. Exponents and powers make calculating easier because you don't have to
write the number down multiple times, especially with big or repeated
numbers. You can use a shorthand. It makes working with significant
numbers in science, engineering, or even simple applications like
calculating interest or energy usage is much easier.

13. For instance:​
- Instead of multiplying 10 x 10 x 10 x 10 to get 10,000, you write 10^4,
which stands for 10,000.
Now with exponents and powers under your belt, you are going to solve
problems fast and be innovative and discover patterns in math.
Difference Between Exponent and Power Functions

14. Exponents and powers are two closely related mathematical functions
often used in the same context, yet with different meanings and purposes
of application. Each term must be defined and considered in its application
to understand their differences.
An exponent rule is called a small number placed above and to the right of
a base number to indicate how many times to multiply the base by itself.
Exponents important rules are meant to be practised timely.

15. A power is called as the result of that multiplication. In other words, the
exponent is the instruction, and the power is the result. It can also be
regarded as a superscript number. It is mentioned up right the number.
For instance, in (3^4 = 81), 4 is the positive exponent part, 3 is the base, and
81 is the power. Exponents focus on the repeated multiplication process. It
is repeated multiplication with the same factor. Hence, the correct answer
is 81.
They tell us how often the base number is used as a factor. For example, in
(2^5), the exponent 5 instructs us to multiply (2 times 2 times 2
times 2 times 2 = 32). This process of repeatedly multiplying is the
key to understanding how exponents work.
Exponents are, therefore, an operation, such as addition or multiplication,
that indicates "how many times." They do not generate the final number but
rather form the means of obtaining it. Powers, on the other hand, are the

16. product of applying the exponent to a base number. If exponents are the
instructions, powers are the final answers.
For example, in (5^3), the exponent 3 tells us to multiply (5 times 5 times 5),
and the power is the resulting number, 125. Powers are the quantities we
interpret or use in further calculations. While exponents define the
operation, powers encapsulate the completed result of that operation,
making them the output of the mathematical process.
The relationship between exponents and powers is interdependent but
distinct. The exponents provide a rule or structure, but the powers are the
values you get from using it. It is similar to baking; an exponent offers a
recipe with the number of ingredients to take (base) and the number of
times to mix (exponent), but the power will be the final baked goods.
This distinction (main the difference between exponent and) is crucial in
advanced mathematics, where powers often serve as the basis for further
operations, such as solving equations, plotting graphs, or analyzing data

17. trends. Understanding the distinction between exponents and powers helps
students grasp the broader applications of both. Exponents simplify writing
and calculating large or small numbers efficiently. Powers, being the
outcomes, allow us to represent results compactly and use them in
practical scenarios. For instance, calculating the rate of growth of
investments, scientific measurements, or engineering problems often
require the use of exponents and powers to interpret.
Although the terms are used interchangeably in more casual contexts,
understanding both their distinct roles will always enrich understanding
and strengthen mathematics problem-solving skills.
Exponent Vs Power
Exponents and powers are probably some of the most familiar and closely
related yet unique mathematical concepts regarding their definitions,
representations, and applications. An exponent is a small number that is
placed above and to the right of a base number indicating how many times

18. the base needs to be multiplied by itself, whereas a power is the outcome
of that process. These may be minor, but these differences helpus
understand how they are utilized in mathematical calculations and
applications. There can be two exponents as well.
Definitions
An exponent is a mathematical notation that signifies repeated
multiplication of a base number. For example, in the equation (2^3), the
exponent is 3, directing us to multiply the base (2) three times: (2 times 2
times 2). The power, however, refers to the result of the operation. Using
the same example, the power is 8, which is the outcome of the calculation.
Essentially, exponents represent the process, while powers represent the
final result.
Representation The representation of exponents and powers is another
way to distinguish between them.

19. The general format for an exponent is (a^n), where (a) is the base, and
(n) is the exponent.​
On the other hand, Powers refer to the value produced upon performing the
operation that the exponent indicates. In (3^4 = 81), the expression
(3^4) is the base with an exponent, while 81 is the power. It is a subtle
distinction in that powers are the quantities that are generated as the result
of applying exponents.
Exponents make it easier to express big or repeated multiplications. We do
not have to write (10 times 10 times 10 times 10) but instead use
the expression as (10^4). Since powers are the result, they are usually
used in further mathematical operations. Suppose that (10^4 = 10,000).
Then we can use the power 10,000 in subsequent calculations, like
calculating the total cost or measuring distance.
Definition

20. An exponent is a mathematical notation that signifies repeated
multiplication of a base number. For example, in 232^323, the exponent is
3, which directs us to multiply the base 222 three times (2×2×22 times 2
times 22×2×2). A power, on the other hand, is the result of this operation.
Using the same example, the power is 8, which is the outcome of the
calculation. Essentially, exponents represent the process, while powers
represent the final result.
Exponents can be there in the form of variables as well like m n.
Representation
The representation of exponents and powers is another way to distinguish
between them. The general format for an exponent is ana^nan, where aaa
is the base, and nnn is the exponent. Powers, however, refer to the specific
value obtained after carrying out the operation dictated by the exponent. In
34=813^4 = 8134=81, the term 343^434 includes both the base and the
exponent, while 81 is the power. This distinction emphasizes that powers

21. are the numerical results produced by using powers and exponents
together.
Usage in Simplification
Exponents simplify the expression of large or repeated multiplications.
Instead of writing 10×10×10×1010 times 10 times 10 times
1010×10×10×10, we can represent this as 10410^4104. Powers, being the
outcome, are often used in subsequent mathematical calculations. For
example, if 104=10,00010^4 = 10,000104=10,000, the power 10,000 can be
applied in further computations, such as finding the total cost or measuring
distance.
Examples to Demonstrate Differences
Let’s consider a few examples:

22. 1.​ In 25=322^5 = 3225=32, the exponent is 5, instructing us to multiply
222 five times. The power is 32, which is the result.
2.​ In 53=1255^3 = 12553=125, the base is 5, the exponent is 3, and the
power is 125. Here, 125 is the final numerical value after applying the
exponentiation process. This is a case of larger number.
Role in Scientific Notation
Graphical Representation
Zero and Negative Exponents
Exponents also include special rules, such as zero and negative exponents.
For instance, 20=12^0 = 120=1 because any non-zero number raised to the
power of zero is 1.