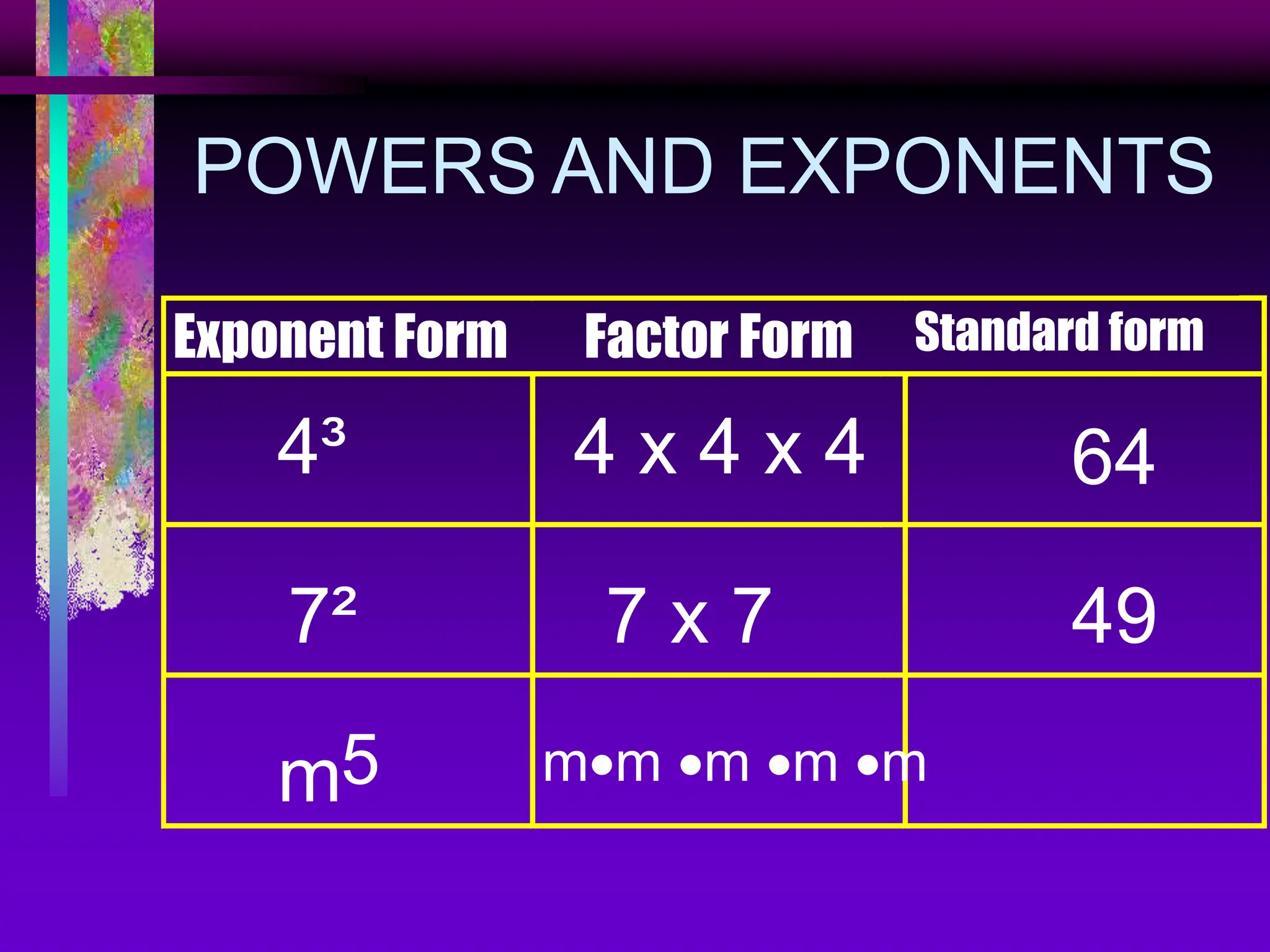
The document covers the concepts of exponents and powers, defining key terms such as base, exponent, and different forms of representing numbers. It elaborates on the laws of exponents, including multiplication, division, and zero exponent rules, along with examples illustrating these concepts. Additionally, it provides exercises for application and comparison of large and small numbers expressed in scientific notation.

1. EXPONENTS AND POWERS

2. EXPONENTS AND POWERS
VOCABULARY
• FACTORS - numbers that
are multiplied together.
• BASE - the number being
used as a factor.
• EXPONENT - tells how
many times a number is
used as a factor.

3. POWERS & EXPONENTS
VOCABULARY
• POWER - a number that is
expressed using exponents.
• SQUARED - a number that
has an exponent of 2.
• CUBED - a number that has
an exponent of 3.

4. EXPONENT FORM
2³
base
exponent

5. FACTOR FORM
2³ = 2 x 2 x 2
factors

6. STANDARD FORM
2³ = 2 x 2 x 2
8
4 x 2

7. POWERS AND EXPONENTS
Exponent Form Factor Form Standard form
4³ 4 x 4 x 4 64
7² 7 x 7 49
m5 mm m m m

8. Follow Order of Operations
5 + 3² - 8
5 + 3 x 3 - 8
5 + 9 - 8
14 - 8
6

9. What is the value of m² + n³,
if m=4 and n =5?
4² + 5³
4 x 4 + 5 x 5 x 5
16 + 5 x 5 x 5
16 + 25 x 5
16 + 125
141

10. A light year is the distance
light travels in one year. The
Milky Way galaxy is about
100,000 light years wide.
Write 100,000 as a power
with 10 as the base.
105

11. Exponents
 3
5
power
base
exponent
3 3
means that is the exponential
form of t
Example:
he number
125 5 5
.
125


12. Zero and Negative Exponents
DEFINITION OF NEGATIVE EXPONENTS
a-n is the reciprocal of an.
n
n
a
a
1


, where a is not
equal to 0.

13. Example
What this really means is that you turn a negative exponent
into a positive exponent by shifting the power from
numerator to denominator or vice versa!
2
2
1 1
2
2 4

 
3
3
1 1
4
4 64

 
Important – only move the base number and the negative exponent
that goes with it!

14. NUMBERS WITH
NEGATIVE EXPONENTS
FOLLOW THE SAME
LAWS OF EXPONENTS

15. The Laws of Exponents:
#2: Multiplicative Law of Exponents: If the bases are the same
And if the operations between the bases is multiplication, then the
result is the base powered by the sum of individual exponents .
m n m n
x x x 
 
3 4 3 4 7
Example: 2 2 2 2

  
   
3 4
7
Proof: 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2
        
      

16. The Laws of Exponents:
#3: Division Law of Exponents: If the bases are the same
And if the operations between the bases is division, then the
result is the base powered by the difference of individual
exponents .
m
m n m n
n
x
x x x
x

  
4
4 3 4 3 1
3
5
Example: 5 5 5 5 5
5

    
4
3
5 5 5 5 5
Proof: 5
5 5 5 5
  

 
 


17. The Laws of Exponents:
#4: Exponential Law of Exponents: If the exponential form
is powered by another exponent, then the result is the base
powered by the product of individual exponents.
 
n
m mn
x x

 
2
3 3 2 6
Example: 4 4 4

 
       
2 2
3
6
Proof: 4 4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4
         
      

18. The Laws of Exponents:
#5: Product Law of Exponents: If the product of the bases
is powered by the same exponent, then the result is a multiplication
of individual factors of the product, each powered by the given
exponent.
 
n n n
xy x y
 
 
2
2 2
2 2
2
Proof: 2 3 4 9
Example: 36 6 2 3 2 3
36
    
   

19. The Laws of Exponents:
#6: Quotient Law of Exponents: If the quotient of the bases
is powered by the same exponent, then the result is both
numerator and denominator , each powered by the given
exponent.
n n
n
x x
y y
 

 
 
3 3
3
2 2
Example:
7 7
 

 
 

20. The Laws of Exponents:
#7: Negative Law of Exponents: If the base is powered by the
negative exponent, then the base becomes reciprocal with the
positive exponent.
1
m
m
x
x


3
3
1 1
Example #1: 2
2 8

 
3
3
3
1 5
Example #2: 5 125
5 1

  

21. The Laws of Exponents:
#8: Zero Law of Exponents: Any base powered by zero exponen
equals one
0
1
x 
1120 = 1 a0 = 1

22. USE OF
EXPONENTS TO
EXPRESS SMALL
NUMBERS IN
STANDARD
NUMBER

23. THE DISTANCE FROM EARTH TO SUN IS
149,600,000,000 m =
1.496 X 1011
THE SPEED OF LIGHT IS 300,000,000m/sec =
3 X 1011
THE AVERAGE DIAMETER OF A RED
BLOOD CELL IS 0.000007 mm =
7 X 106
THE DISTANCE OF MOON FROM THE
EARTH IS 384,467,000m =
3.84467 X 108
AVERAGE RADIUS OF THE SUN IS 69,55,000
km=
6.955 X 106

24. COMPARING VERY
LARGE AND VERY
SMALL NUMBERS

25. The diameter of the Sun is 1.4 X 109 m and the
diameter of the Earth is 1.2756 X 107 m .
Suppose you want to compare the diameter , with the
diameter of the Sun.
Diameter of the Sun = 1.4 X 10 9 m
Diameter of the Earth = 1.27556 X 10 7 m
Therefore 1.4 X 10 9
1.27556 X 10 7
= 1.4 X 10 9-7
1.2756
= 1.4 X 100
1.2756
Which is approximately 100 times the diameter of the
earth .

26. MULTIPLE CHOICE QUESTIONS
(i) ( a/b) m
(a) abm
(b) am / bm
(ii) 5-1 X 3 is
(a) 3/5
(b) 5/3
(iii) The value of 1a X ma
(a) 1
(b) ma
(iv) The standard form of 1.870000 is
(a) 1.87 X 10 5
(b) 1.87 X 106

27. (v) 13 5÷ 169 is equal to
(a) 137
(b) 133
(vi) The reciprocal of (32)4
(a) 38
(b) 1 / 38
(vii) Compare 5 X 107 ; 6 X 10 4
(a) 5 X 107 is greater
(b) 6 X 10 4 is greater
(viii)Find the value of 34 X 9
(a) 36
(b) 34

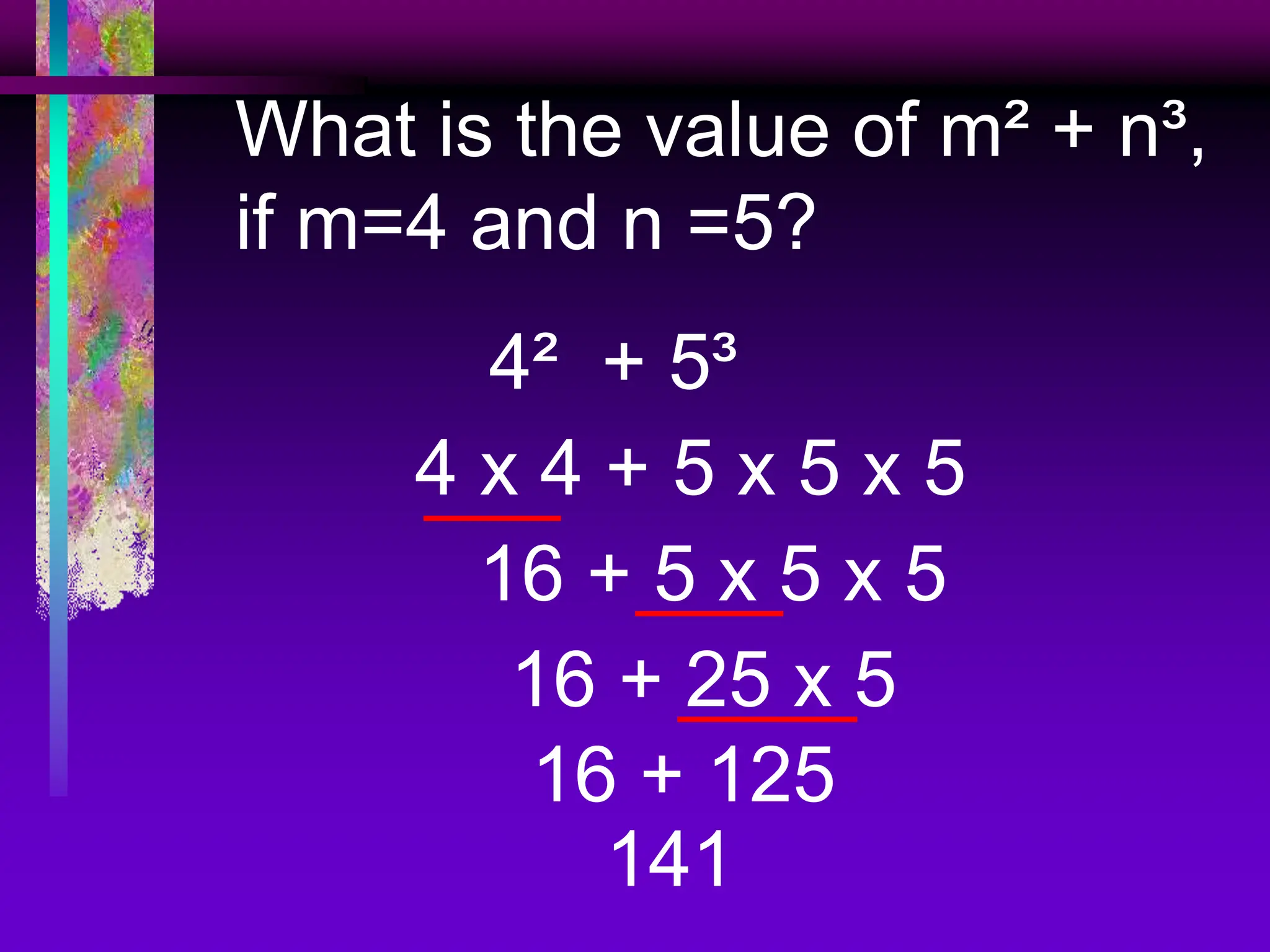
28. Find the value of n :
𝑎5
𝑎3 X [ a8 ] = (a n-6 )
Solution :
= a5-3 x a 8 = a n-6 [ am ÷ an = a m-n ]
= a2 x a8 = an-6
= a 10 = a n-6
= a 10 + 6
Ans. n = 16

29. Q.2 Find the value of X
Solution :
(
3
2
)5 =(
3
2
)2𝑥 + 1
3
2
3+5 =
3
2
2x +1
= 8 = 2x +1
= 8-1 = 2x
= 7 = 2x
Ans .
7
2
= x

30. THANK YOU !