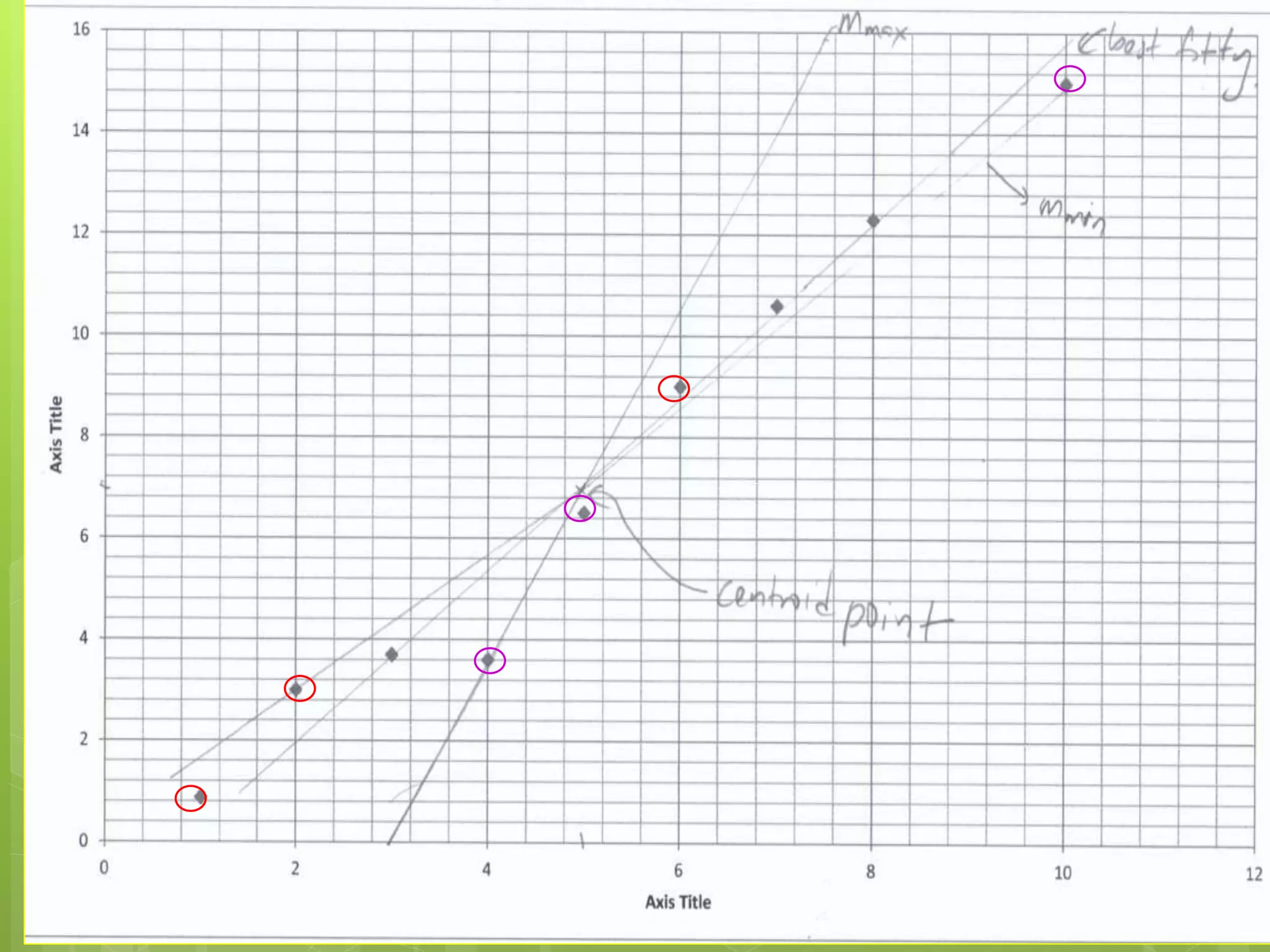
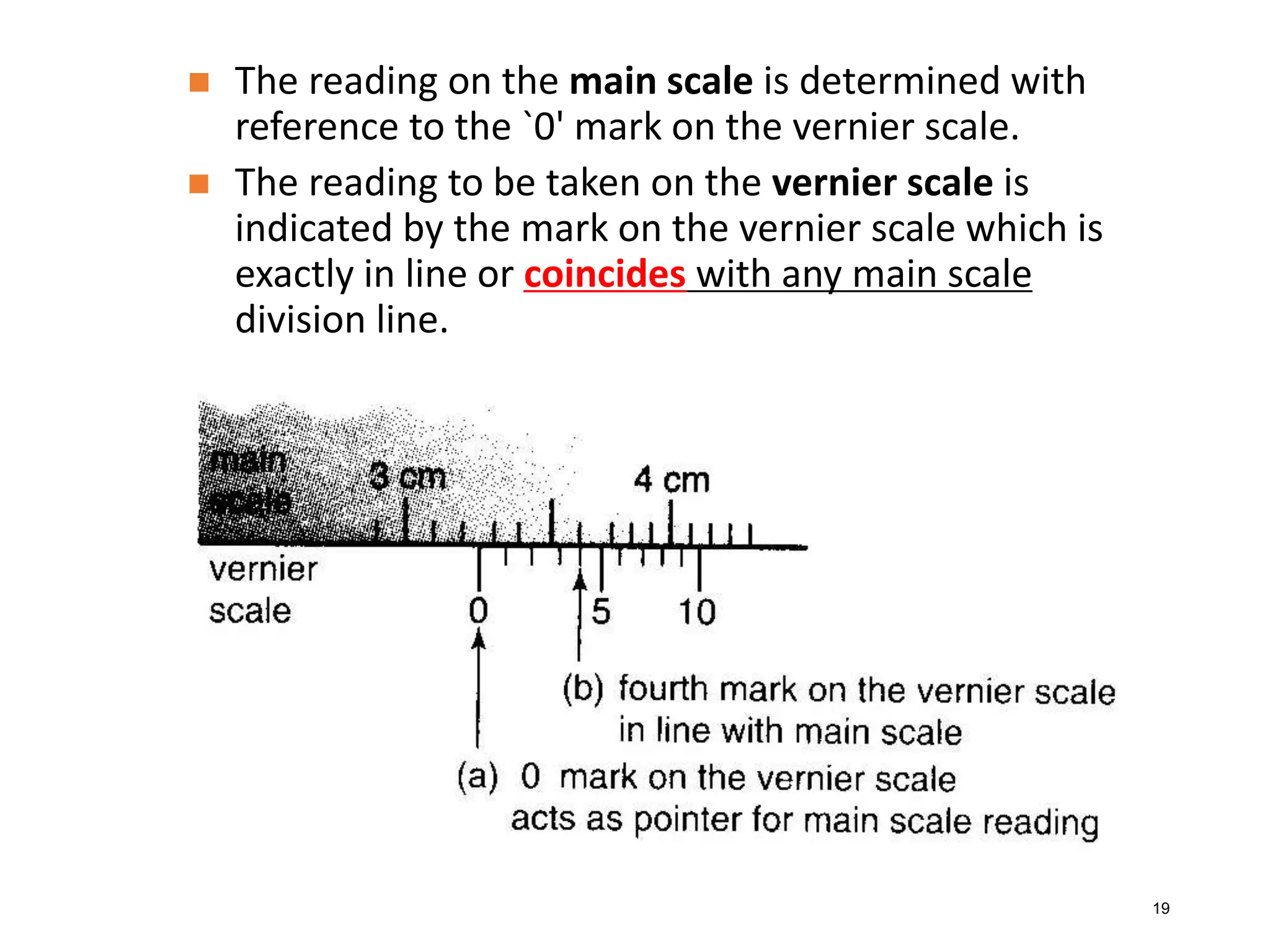
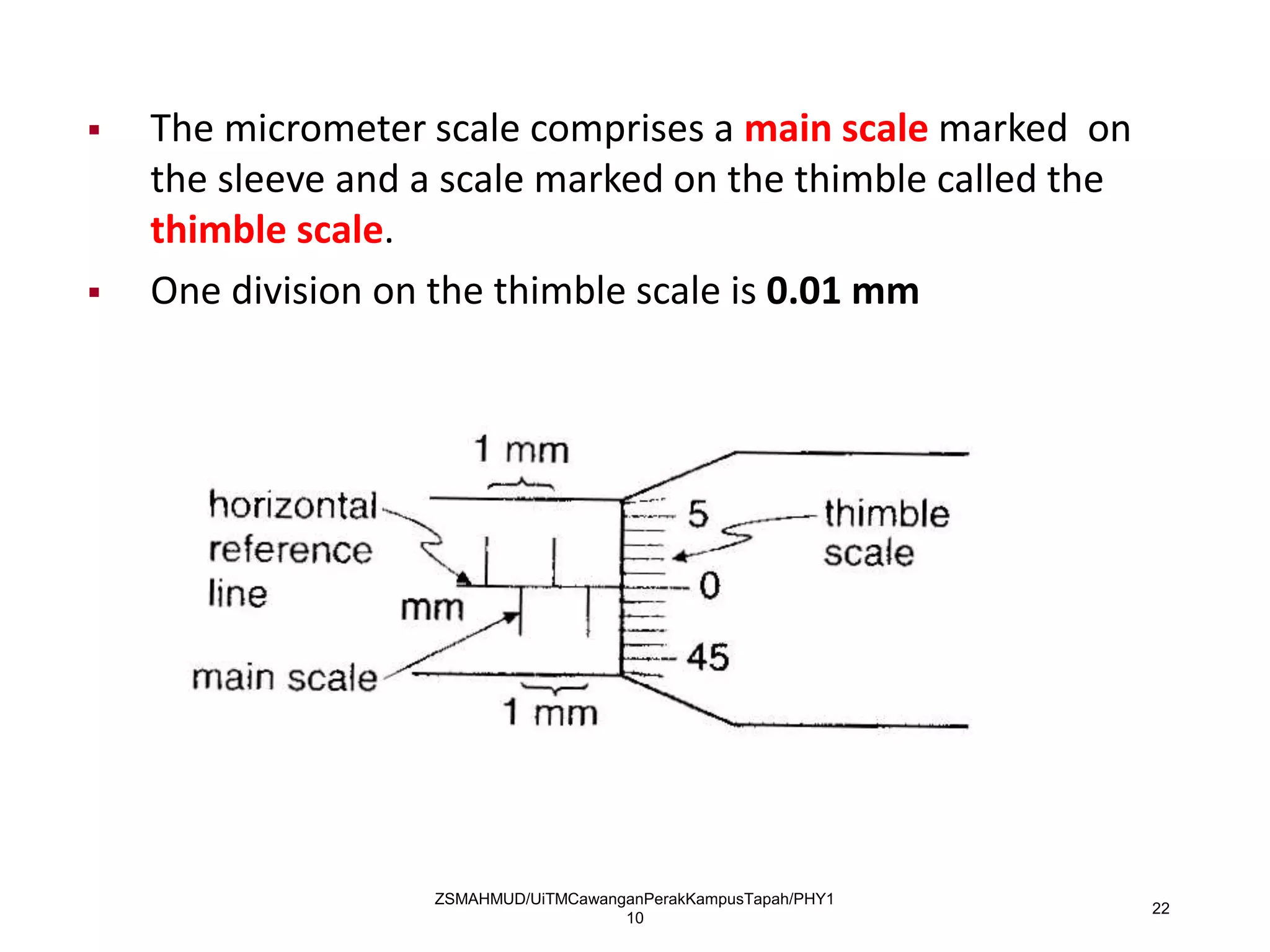
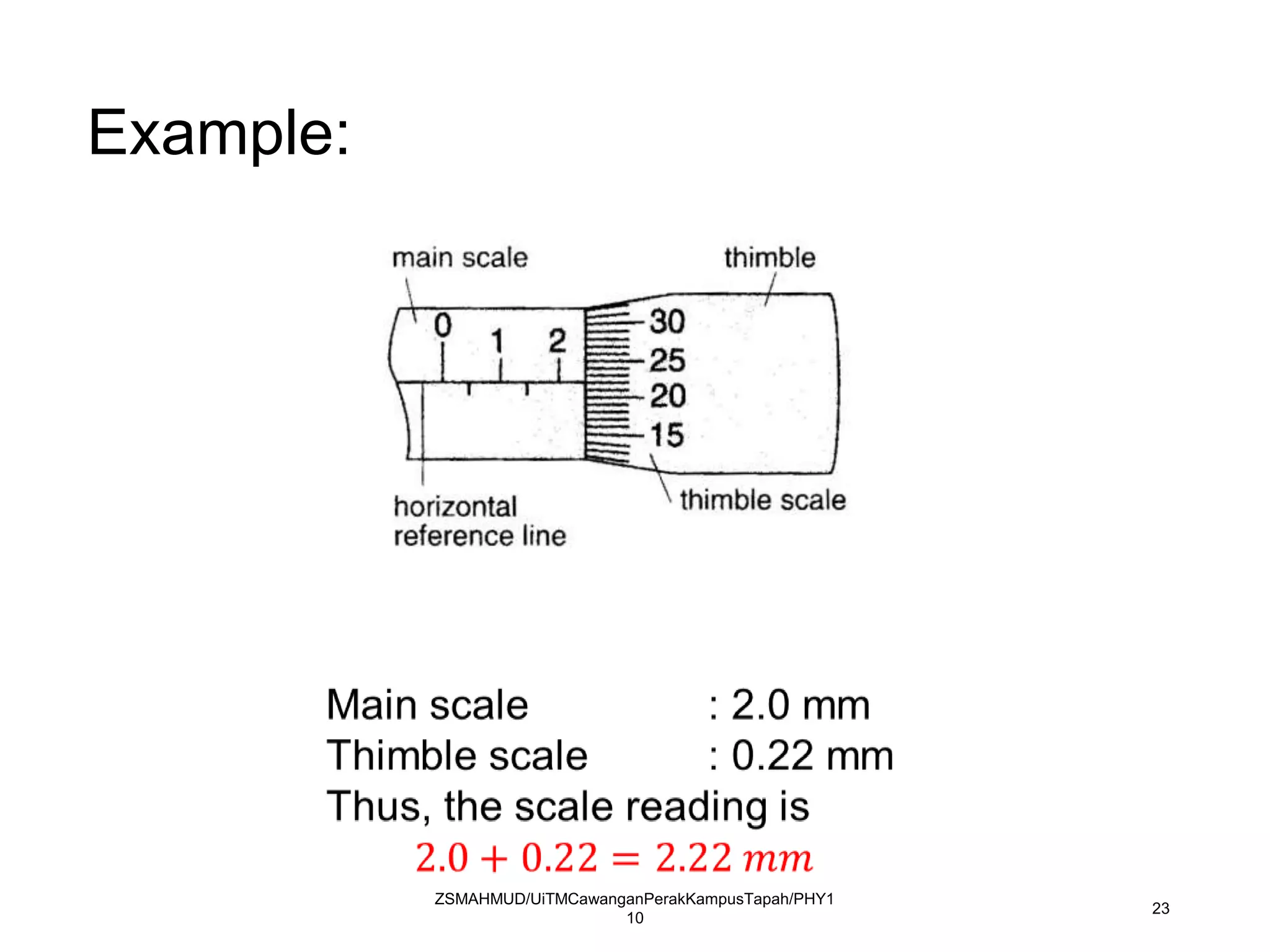
Measurement involves uncertainty from errors and imprecision. An error is the difference between measured and expected values, while uncertainty summarizes the error. Random errors arise from unpredictable fluctuations, and systematic errors are reproducible biases. Accuracy refers to closeness to the true value, while precision reflects consistency of measurements. Uncertainty is quantified from instrument resolution, repeated measurements, or comparison to a standard value. It is calculated and reported with the measurement result.

2. UNCERTAINTY AND ERROR IN
MEASUREMENT
 An error is the difference between the measured
value and the expected value of something
(unavoidable).
 An uncertainty is a way of expressing or
summarizing the error (unavoidable).
 A mistake is simply not doing something correctly
through carelessness (avoidable).
 Thus, an error is not the same as an uncertainty,
though both are unavoidable

3. PRECISION AND ACCURACY
 Accuracy is the closeness of agreement
between a measured value and a true or accepted
value (measurement error reveals
 Precision is a measure of the degree of
consistency and agreement among independent
measurements of the same quantity the amount
of inaccuracy).

4. Type of Error
RANDOM ERRORS refer to random
fluctuations in the measured data due to:
 The readability of the instrument
 The effects of something changing in the
surroundings between measurements
 The observer being less than perfect
SYSTEMATIC ERRORS refer to reproducible fluctuations
consistently in the same direction due to:
 An instrument being wrongly calibrated
 An instrument with zero error (it does not read zero
when it should – to correct for this, the value should be
subtracted from every reading)
 The observer being less than perfect in the same way
during each measurement.

5. ABSOLUTE AND
PERCENTAGE
UNCERTAINTIES
Measurement = measured value ±
uncertainty (unit of measurement)
How?

6. ABSOLUTE AND
PERCENTAGE
UNCERTAINTIES
1. The min value of the smallest scale of the
instrument (scale measurement Error)
Example 1:
The smallest scale is 0.1 cm
Therefore, Δ L = 0.1/2 = 0.05cm
The value of line is , L Δ L = 8.60 ±0.05 cm

7. ABSOLUTE AND
PERCENTAGE
UNCERTAINTIES
The smallest scale is 1 s
Therefore, Δ t = 1/2 = 0.5 s
The measurement 4.5 ± 0.5s
Example 2:

8. ABSOLUTE AND
PERCENTAGE
UNCERTAINTIES
2. If the experimental has different value for
repeating measurement, the uncertainty is
associated with the average of deviation
Example:
a (mm) 1.55 1.52 1.54 1.53
<a> = (1.55 +1.52+1.54+1.53)/4=1.535
Deviation d1 = |1.55-1.535|=0.015
d2 = |1.52-1.535|=0.015
d3 = |1.54-1.535|=0.005
d4 = |1.53-1.535|=0.005
Average, <d> = (0.015+0.015+0.005+0.005)/4=0.01
The measurement, a = (1.535±0.010) mm

9. ABSOLUTE AND
PERCENTAGE
UNCERTAINTIES
3. If we know the standard value. The
uncertainties normally we calculate the
percentage relative error:
Example: g measure = 10.0 m/s2
g standard = 9.81 m/s2
% error =
|g measure−g standard|
g standard
x100% = 1.936%

10. ABSOLUTE AND PERCENTAGE
UNCERTAINTIES
4. For the graphical analysis of data, we use the
maximum and minimum best-fit lines to determine the
final uncertainty.
Example:
Gradient of best fit, m = 9.78 m/s2
Max gradient, mmax = 9.88 m/s2
Min gradient, mmin = 9.72 m/s2
Δ m = ½ (mmax - mmin )
Therefore, gradient m = (9.78±
0.08 ) m/s2
Same method for calculating the intercept

11. ABSOLUTE AND
PERCENTAGE
UNCERTAINTIES
5. Sometimes, the final result involving
mathematical equations, so we need to be
concerned with how we treat uncertainties in
calculated values using experimental data
I. If data are to be added or subtracted, add
the absolute uncertainty:
A = p ± q , ΔA = Δp + Δ q
Example: Mass of empty beaker is (50 ± 1 ) g
Mass of beaker and water is (100 ± 1 ) g
Mass of water = 100-50 = 50 g
Error of m = 1+1 =2 g
Therefore, mass of water = 50 ± 2 g

12. ABSOLUTE AND
PERCENTAGE
UNCERTAINTIES
II. If data are to be multiplied or divided, add
the percentage uncertainty:
A = p x q ,
ΔA
A
=
Δp
p
+
Δ q
q
A = p / q,
ΔA
A
=
Δp
p
+
Δ q
q
Example: the mass of water is mass of water = 50 ±
2 g. The volume of 2.1 ±0.1 m3. Density=?
Error of density is
Δρ
ρ
=
Δm
m
+
Δ V
V
=

13. ABSOLUTE AND
PERCENTAGE
UNCERTAINTIES
III. If data are raised to a power, multiply the
percentage uncertainty by that power:
A = pn ,
ΔA
A
=n
Δp
p
Example: A cylinder has a radius of 1.60 ± 0.01 cm
and a height of 11.5 ± 0.1 cm. Find the volume.
V = π r2 h = π (1.60)2 x 11.5 = 92.488 cm3 = 92 cm3
ΔV
V
=2
Δr
r
+
Δℎ
ℎ
= 2 cm3
V is (92 ± 2 ) cm3

14. Exercises

15. Exercises

16. Exercises
In experiment simple resistor, the following data
obtain.
Find the resistance and its uncertainty.
Voltage (V) Current (A)
1 0.88
2 3
3 3.7
4 3.6
5 6.5
6 9
7 10.6
8 12.3
10 15

18. 18
 A vernier caliper is used to measure an object with
dimensions up to 12 cm with an accuracy of 0.01 cm.
 Comprises of a main scale and a vernier scale.
Examples of Measuring Instruments
-Vernier Calliper

19. 19
 The reading on the main scale is determined with
reference to the `0' mark on the vernier scale.
 The reading to be taken on the vernier scale is
indicated by the mark on the vernier scale which is
exactly in line or coincides with any main scale
division line.

20. ZSMAHMUD/UiTMCawanganPerakKampusTapah/PHY1
10
20
 Example in Figure below:

21. ZSMAHMUD/UiTMCawanganPerakKampusTapah/PHY1
10
21
This instrument can be used to measure
diameters of wires and thicknesses of steel plates
to an accuracy of 0.01 mm.
Examples of Measuring Instruments
-Micrometer Screw Gauge

22. ZSMAHMUD/UiTMCawanganPerakKampusTapah/PHY1
10
22
 The micrometer scale comprises a main scale marked on
the sleeve and a scale marked on the thimble called the
thimble scale.
 One division on the thimble scale is 0.01 mm

23. ZSMAHMUD/UiTMCawanganPerakKampusTapah/PHY1
10
23
Example:

24. Conclusion:
!!!!!!Measurement = measured value ±
uncertainty (unit of measurement)
Or
% Relative error =
|g measure−g standard|
g standard
x100%
!!!!!!