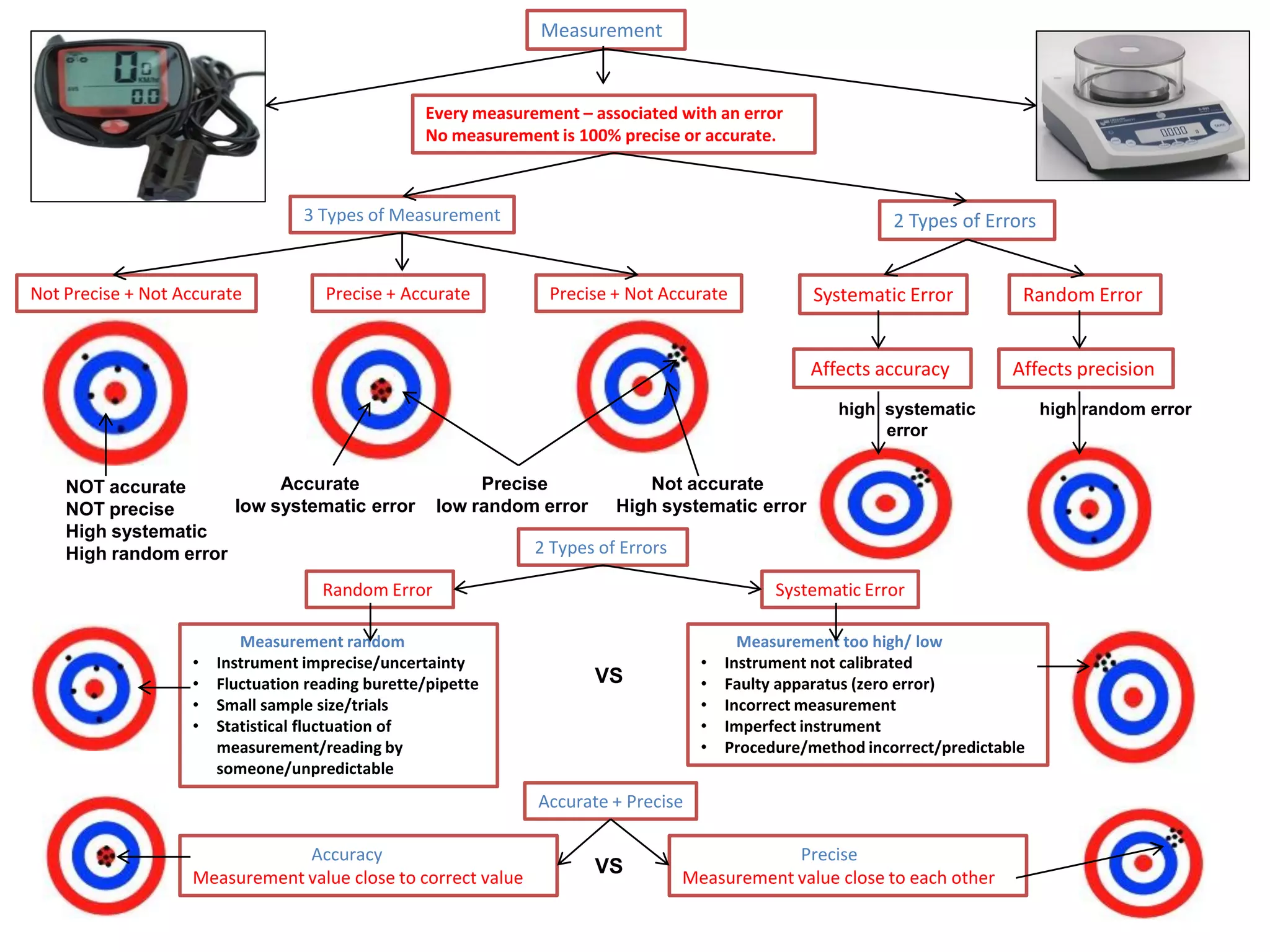
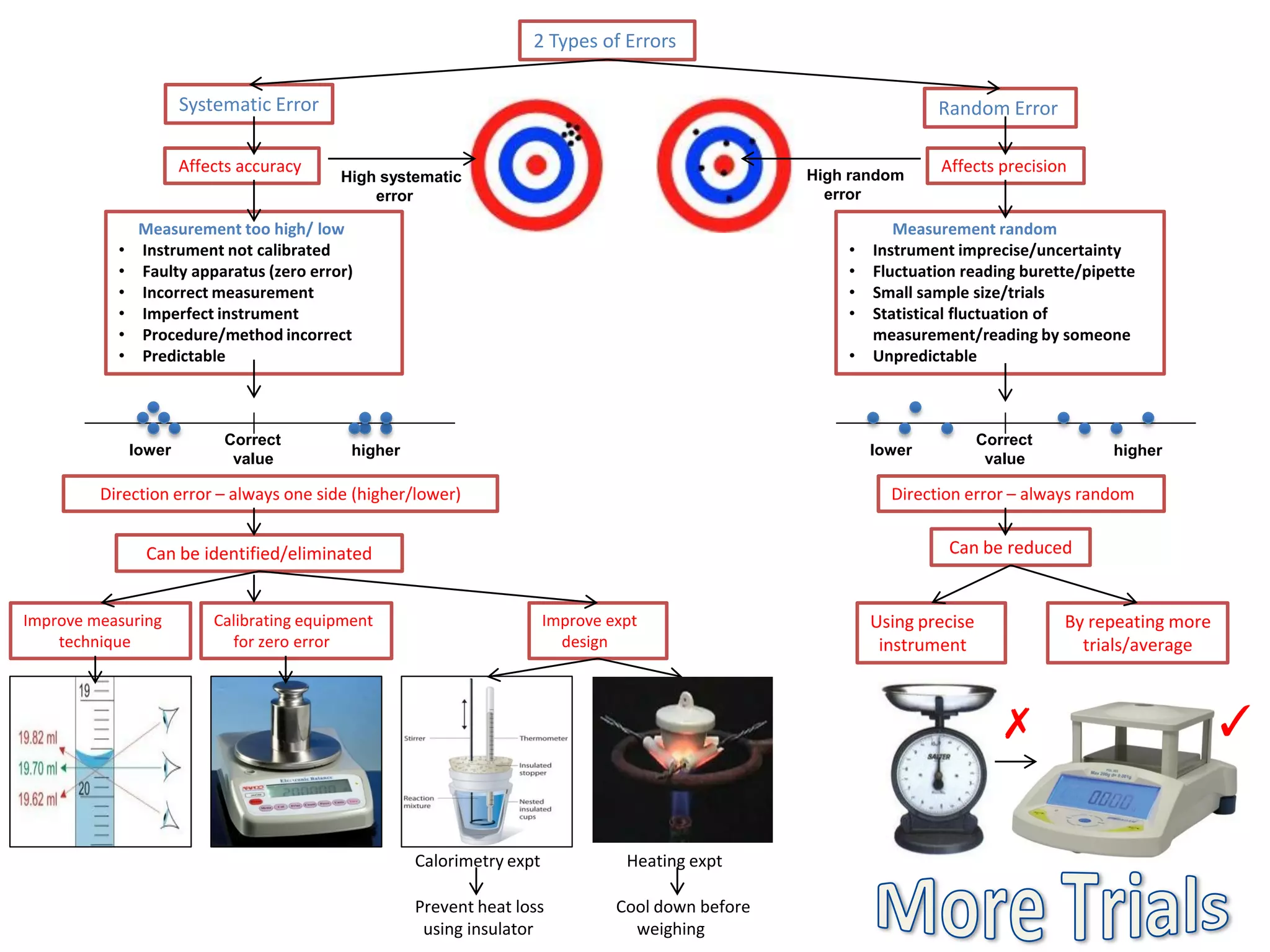
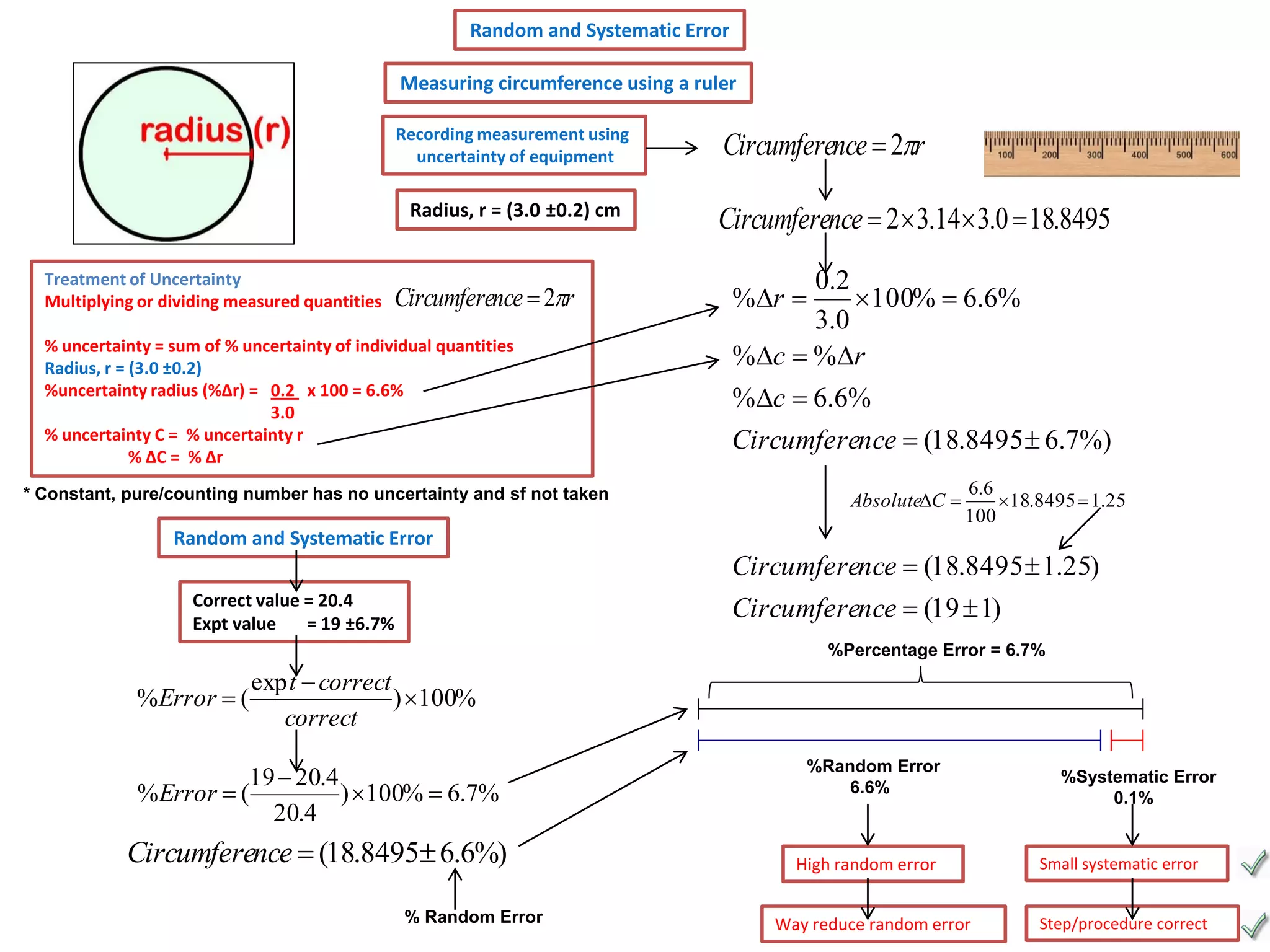
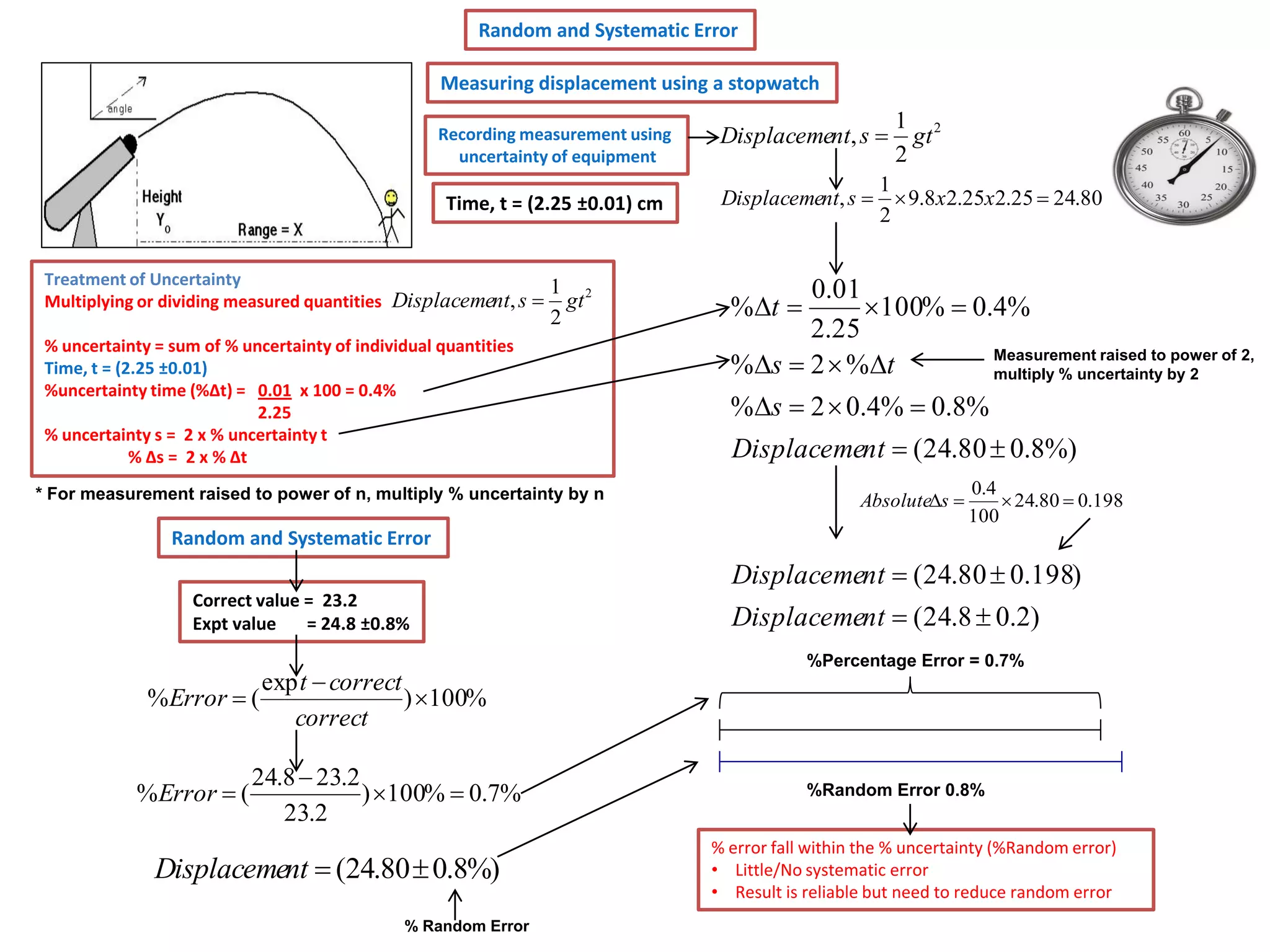
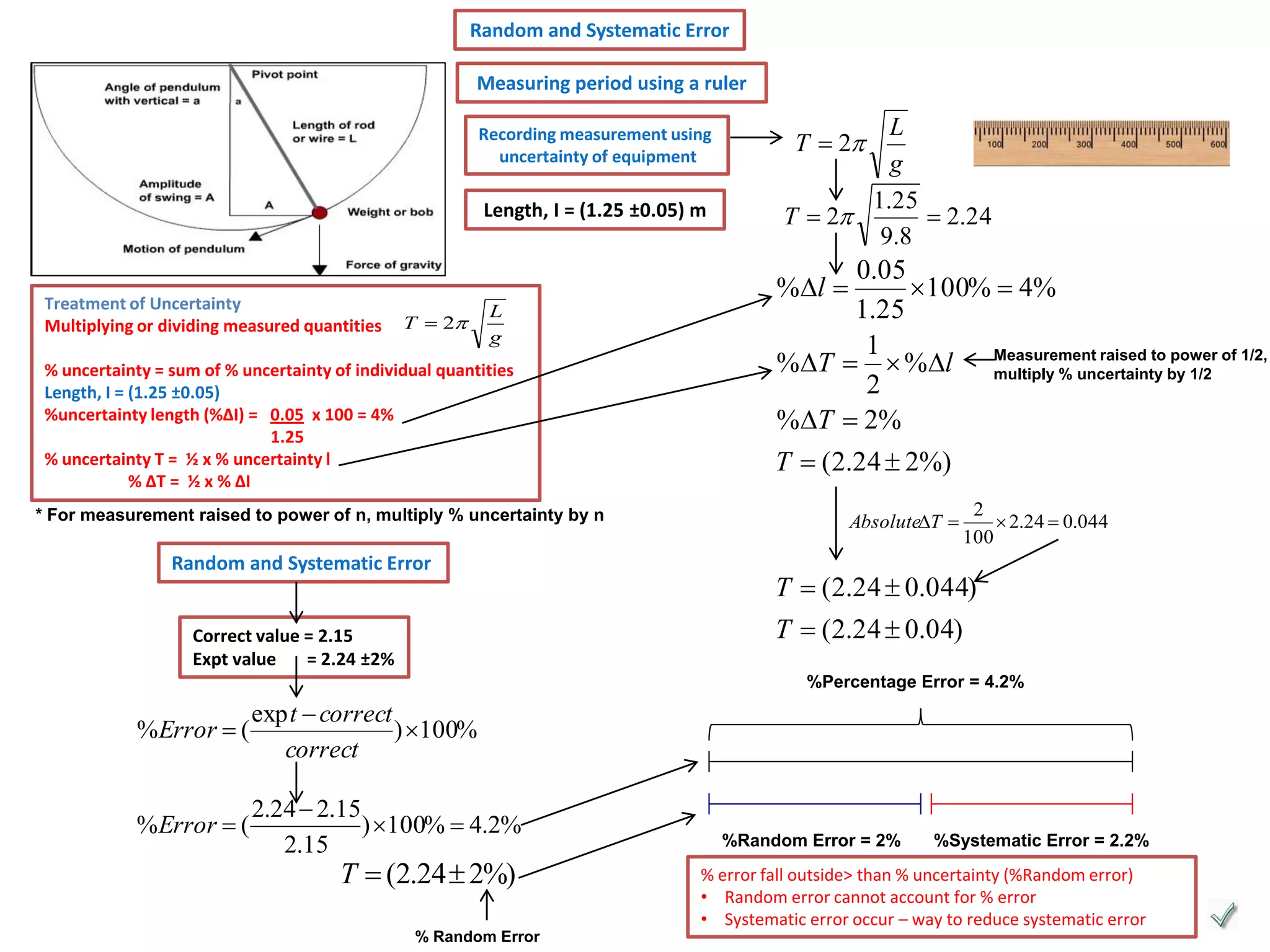
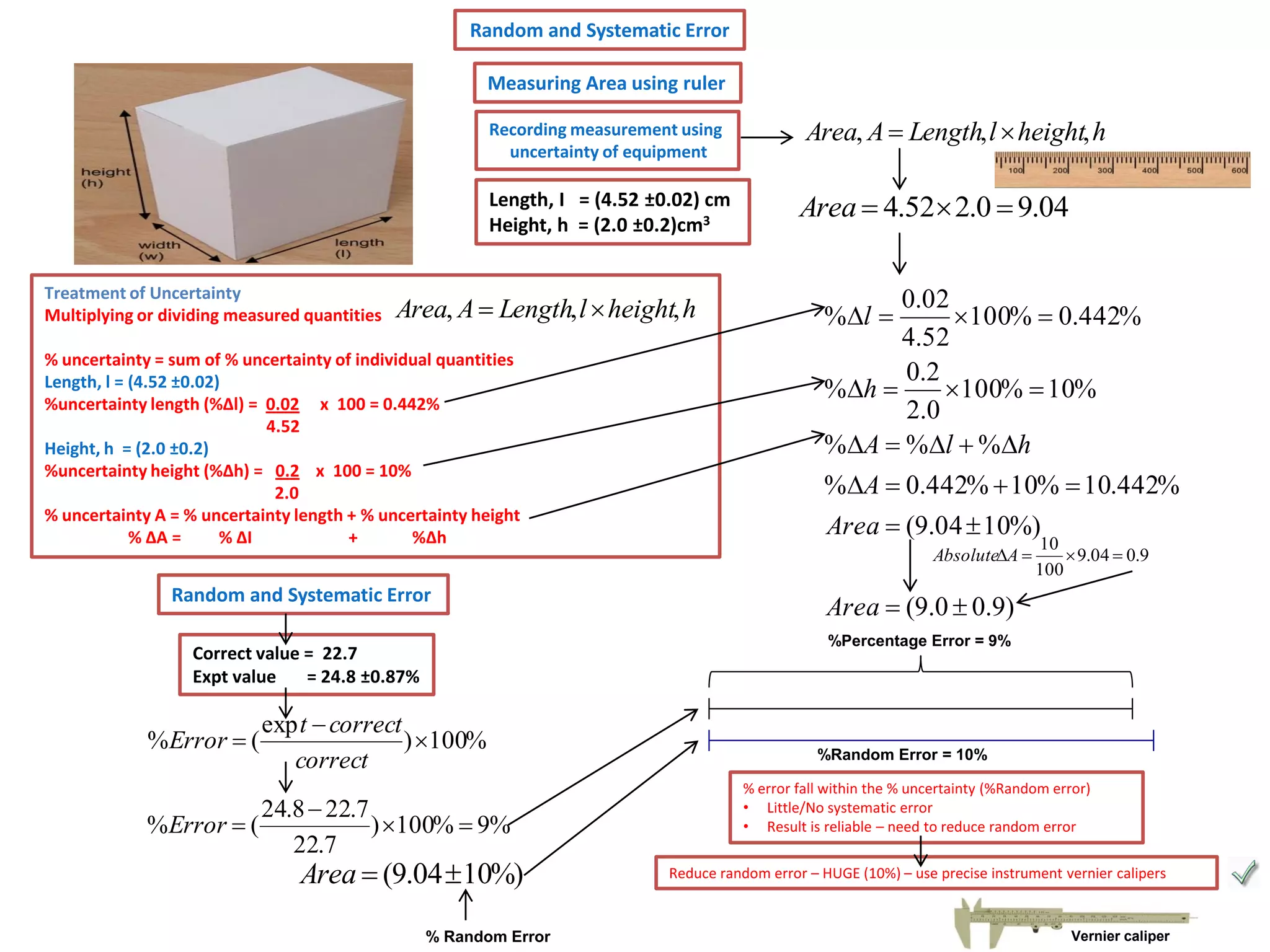
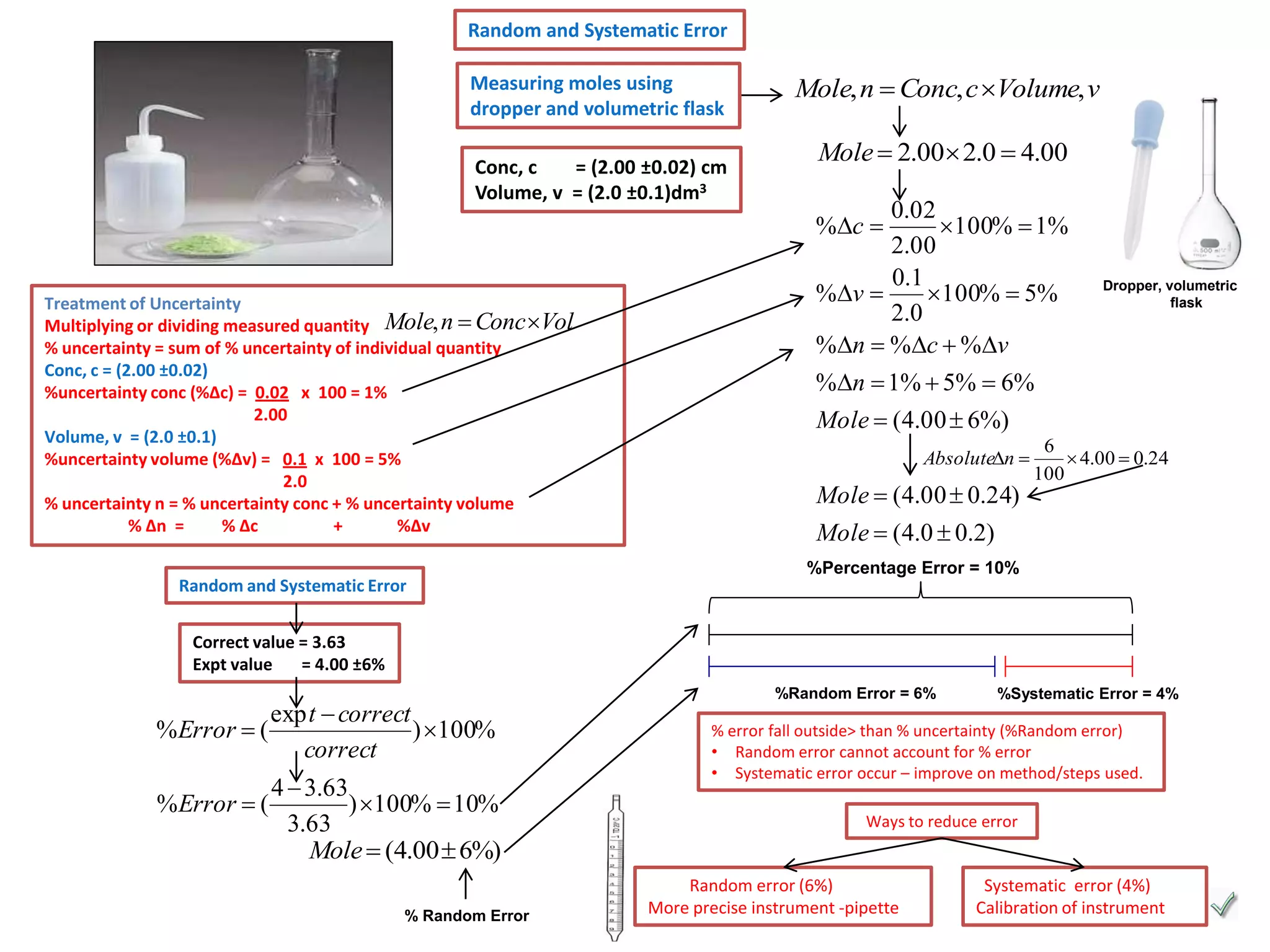
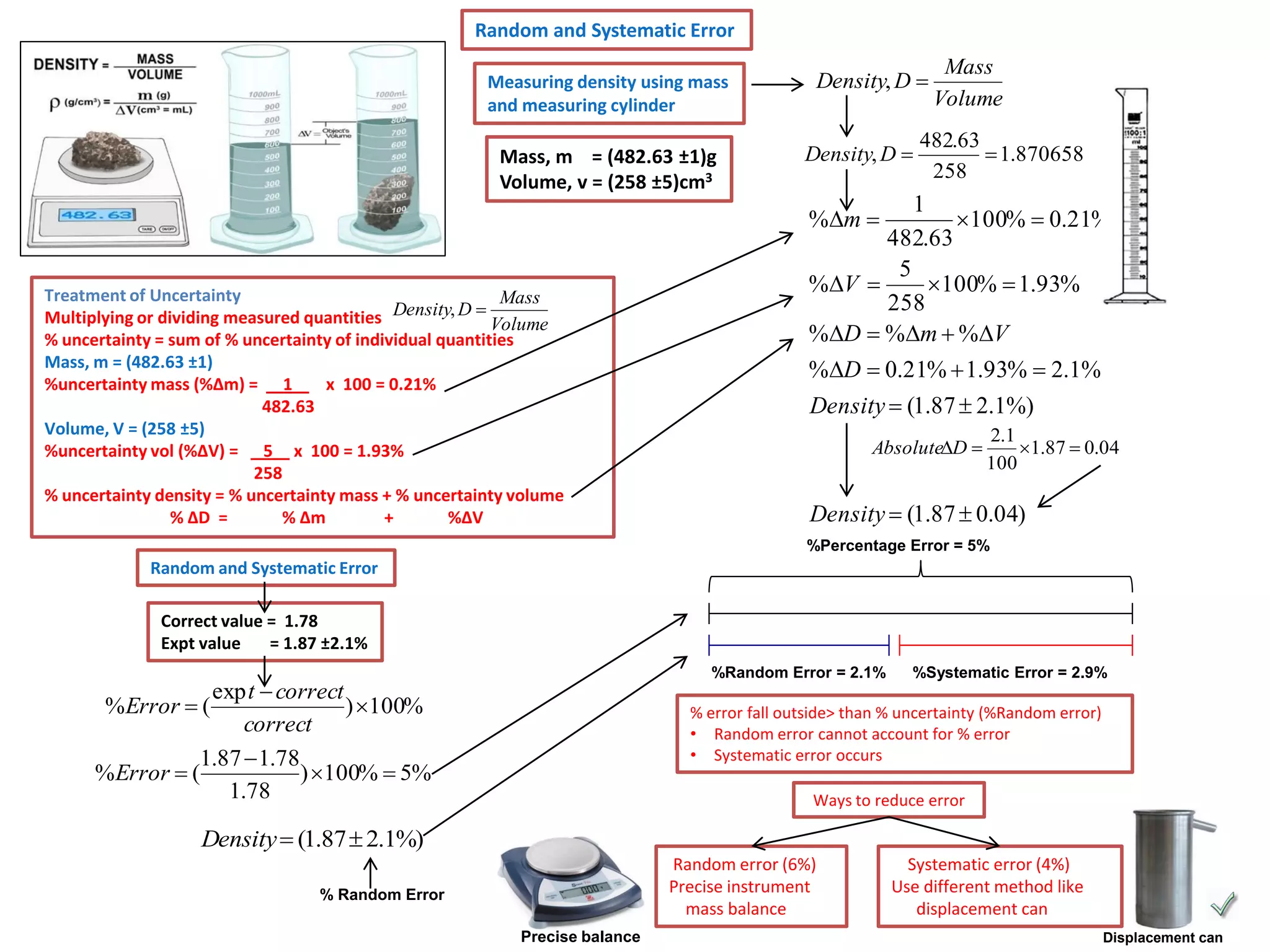
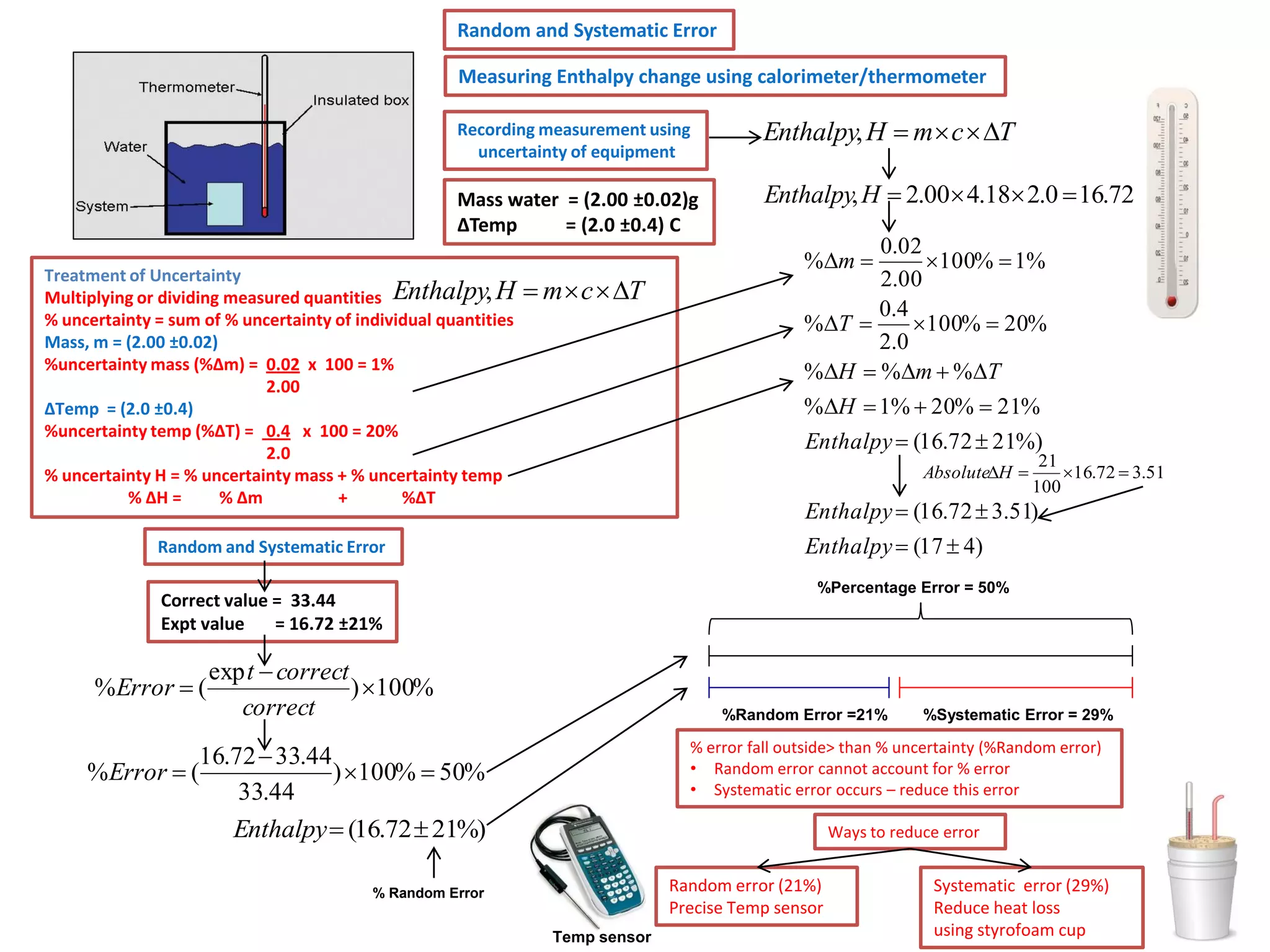
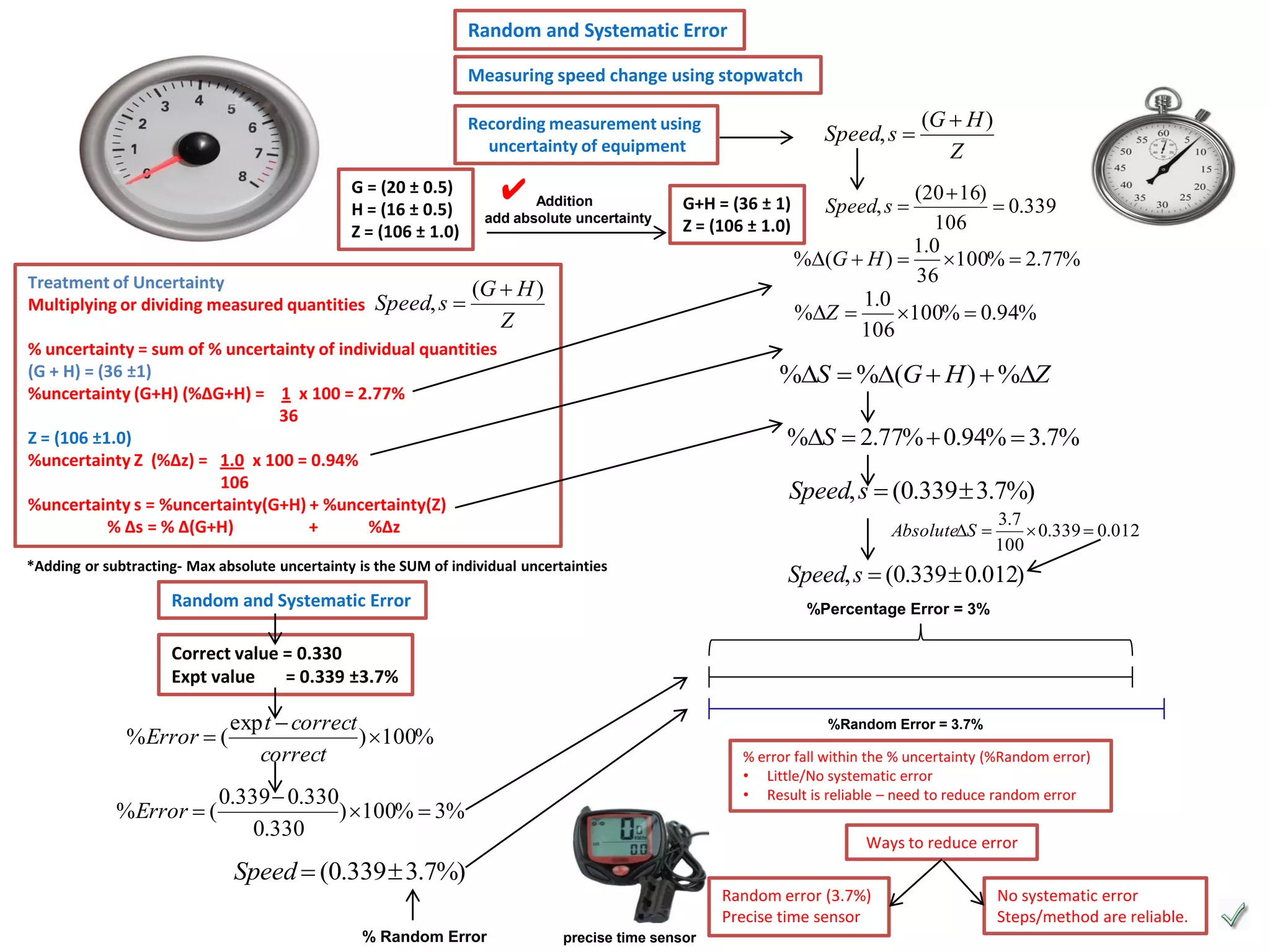
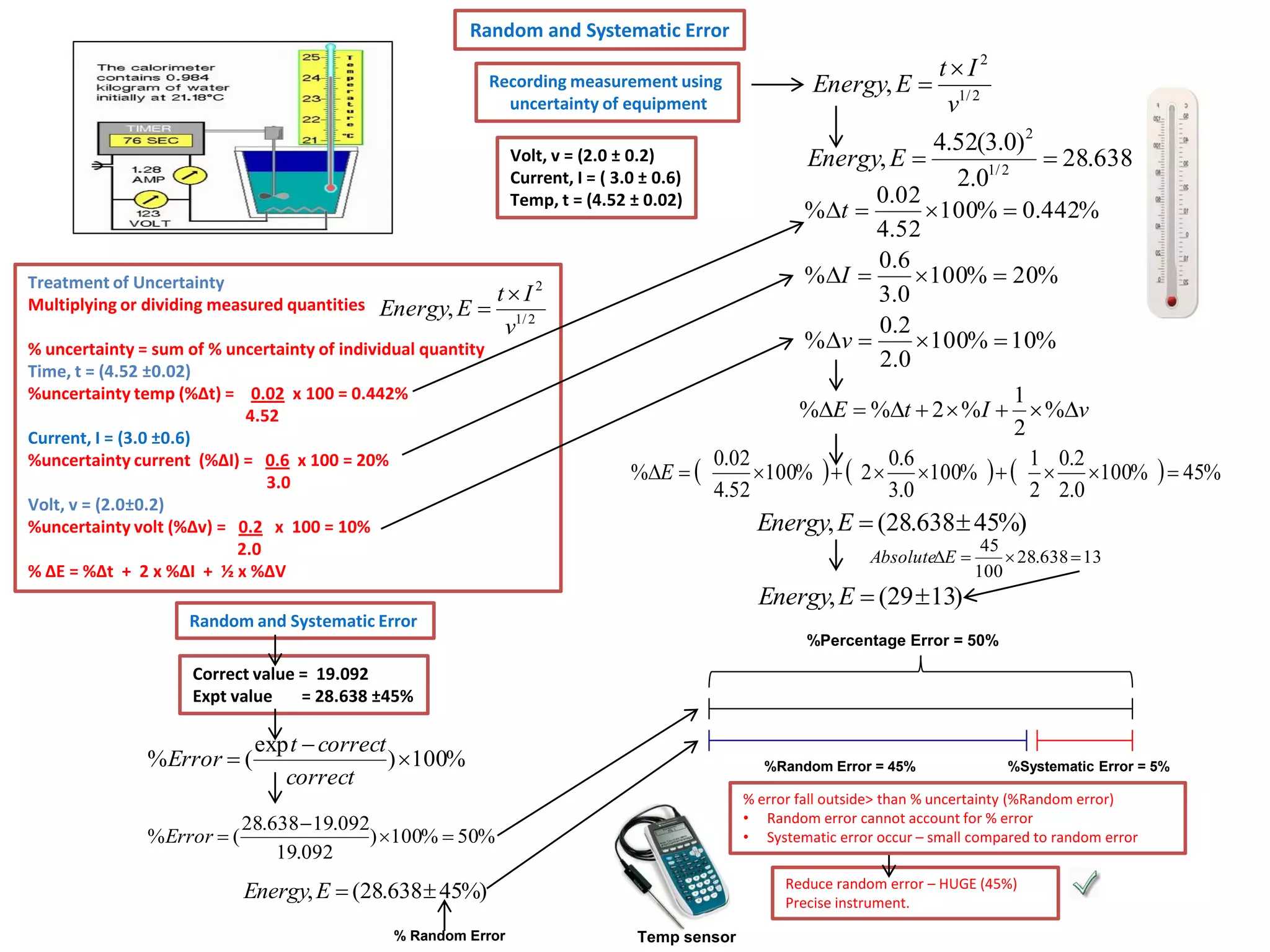
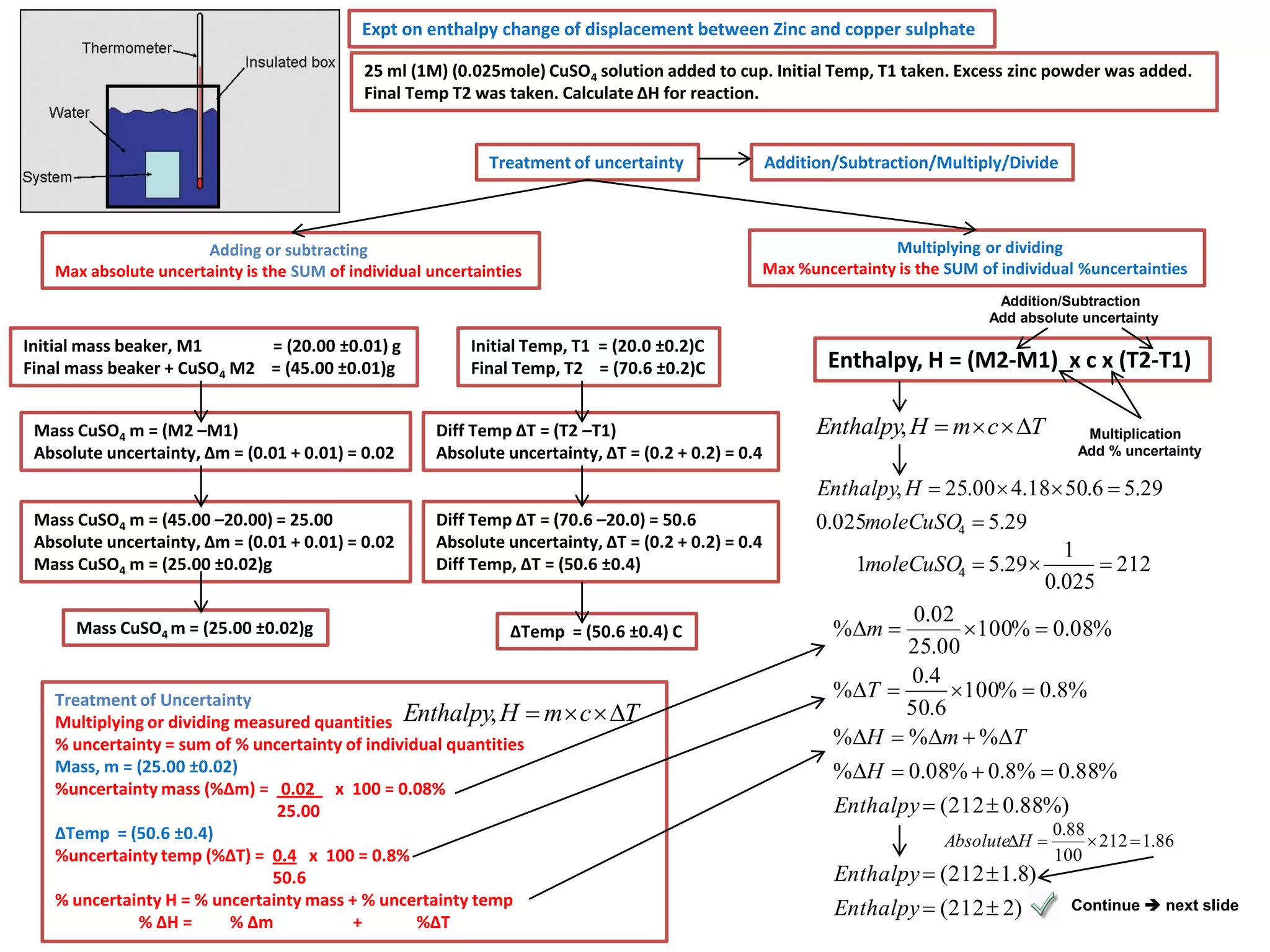
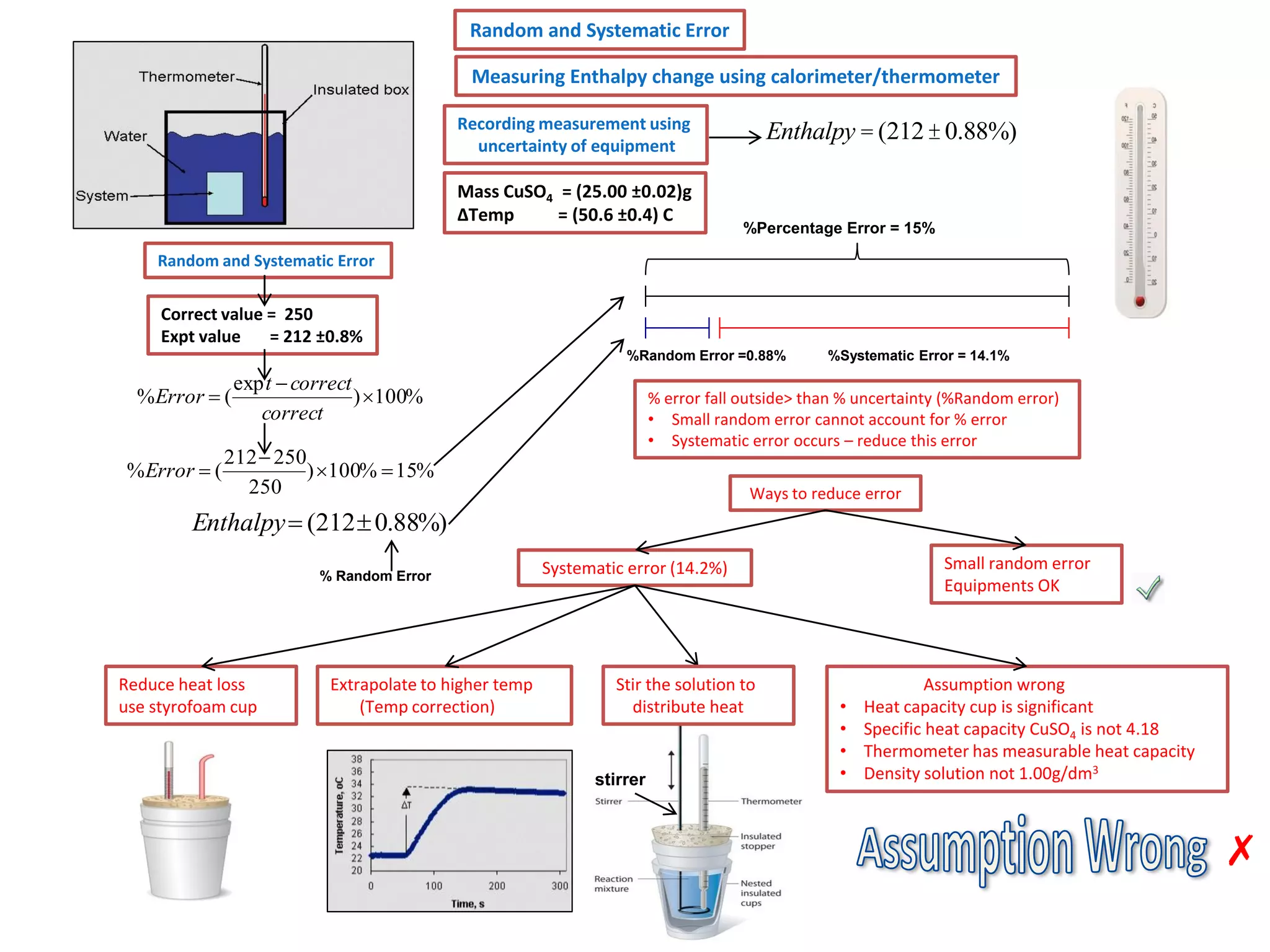
Every measurement has an associated error that affects its precision and accuracy. There are two types of errors - random error and systematic error. Random error affects precision while systematic error affects accuracy. Precision refers to the closeness of repeated measurements while accuracy refers to how close the measurement is to the true value. The percentage uncertainty of a measurement is calculated as the sum of the percentage uncertainties of the individual quantities involved. Measurements with uncertainties that account for the total percentage error are considered reliable while those with uncertainties that do not account for the total percentage error may have unidentified systematic errors. Reducing random errors involves improving measurement techniques while reducing systematic errors involves improving equipment calibration and measurement methods.

1. Measurement
Every measurement – associated with an error
No measurement is 100% precise or accurate.
3 Types of Measurement
Not Precise + Not Accurate
Precise + Accurate
2 Types of Errors
Precise + Not Accurate
Systematic Error
Random Error
Affects accuracy
Affects precision
high systematic
error
Accurate
NOT accurate
low systematic error
NOT precise
High systematic
High random error
Precise
low random error
Not accurate
High systematic error
2 Types of Errors
Random Error
•
•
•
•
Measurement random
Instrument imprecise/uncertainty
Fluctuation reading burette/pipette
Small sample size/trials
Statistical fluctuation of
measurement/reading by
someone/unpredictable
Systematic Error
•
•
•
•
•
VS
Measurement too high/ low
Instrument not calibrated
Faulty apparatus (zero error)
Incorrect measurement
Imperfect instrument
Procedure/method incorrect/predictable
Accurate + Precise
Accuracy
Measurement value close to correct value
VS
Precise
Measurement value close to each other
high random error

2. 2 Types of Errors
Systematic Error
Affects accuracy
•
•
•
•
•
•
Random Error
High random
error
High systematic
error
Measurement too high/ low
Instrument not calibrated
Faulty apparatus (zero error)
Incorrect measurement
Imperfect instrument
Procedure/method incorrect
Predictable
lower
Correct
value
•
•
•
•
•
Measurement random
Instrument imprecise/uncertainty
Fluctuation reading burette/pipette
Small sample size/trials
Statistical fluctuation of
measurement/reading by someone
Unpredictable
Correct
value
lower
higher
Direction error – always one side (higher/lower)
higher
Direction error – always random
Can be reduced
Can be identified/eliminated
Improve measuring
technique
Affects precision
Calibrating equipment
for zero error
Improve expt
design
Using precise
instrument
By repeating more
trials/average
✗
Calorimetry expt
Prevent heat loss
using insulator
Heating expt
Cool down before
weighing
✓

3. Random and Systematic Error
Measuring circumference using a ruler
Recording measurement using
uncertainty of equipment
Radius, r = (3.0 ±0.2) cm
Treatment of Uncertainty
Multiplying or dividing measured quantities
Circumference  2r
% uncertainty = sum of % uncertainty of individual quantities
Radius, r = (3.0 ±0.2)
%uncertainty radius (%Δr) = 0.2 x 100 = 6.6%
3.0
% uncertainty C = % uncertainty r
% ΔC = % Δr
* Constant, pure/counting number has no uncertainty and sf not taken
Random and Systematic Error
Correct value = 20.4
Expt value
= 19 ±6.7%
Circumference  2r
Circumference  2  3.14 3.0  18.8495
0.2
100%  6.6%
3.0
%c  %r
%c  6.6%
Circumference  (18.8495  6.7%)
%r 
AbsoluteC 
6.6
18.8495  1.25
100
Circumference  (18.8495  1.25)
Circumference  (19  1)
%Percentage Error = 6.7%
%Error  (
exp t  correct
) 100%
correct
19  20.4
% Error  (
) 100%  6.7%
20.4
Circumference  (18.8495 6.6%)
% Random Error
%Random Error
6.6%
High random error
Way reduce random error
%Systematic Error
0.1%
Small systematic error
Step/procedure correct

4. Random and Systematic Error
Measuring displacement using a stopwatch
Recording measurement using
uncertainty of equipment
Time, t = (2.25 ±0.01) cm
Treatment of Uncertainty
1 2
Multiplying or dividing measured quantities Displacement, s  gt
2
% uncertainty = sum of % uncertainty of individual quantities
Time, t = (2.25 ±0.01)
%uncertainty time (%Δt) = 0.01 x 100 = 0.4%
2.25
% uncertainty s = 2 x % uncertainty t
% Δs = 2 x % Δt
* For measurement raised to power of n, multiply % uncertainty by n
Displacement, s 
1 2
gt
2
1
Displacement, s   9.8 x2.25x2.25  24.80
2
0.01
100%  0.4%
2.25
Measurement raised to power of 2,
%s  2  %t
multiply % uncertainty by 2
%s  2  0.4%  0.8%
Displacement  (24.80  0.8%)
%t 
Absolutes 
0.4
 24.80  0.198
100
Random and Systematic Error
Correct value = 23.2
Expt value
= 24.8 ±0.8%
exp t  correct
%Error  (
) 100%
correct
%Error  (
24.8  23.2
) 100%  0.7%
23.2
Displacement  (24.80  0.8%)
% Random Error
Displacement  (24.80  0.198)
Displacement  (24.8  0.2)
%Percentage Error = 0.7%
%Random Error 0.8%
% error fall within the % uncertainty (%Random error)
• Little/No systematic error
• Result is reliable but need to reduce random error

5. Random and Systematic Error
Measuring period using a ruler
Recording measurement using
uncertainty of equipment
Length, I = (1.25 ±0.05) m
Treatment of Uncertainty
Multiplying or dividing measured quantities
L
g
1.25
T  2
 2.24
9. 8
T  2
0.05
100%  4%
1.25
1
power
%T   %l Measurement raised to by 1/2 of 1/2,
multiply % uncertainty
2
%T  2%
%l 
T  2
L
g
% uncertainty = sum of % uncertainty of individual quantities
Length, I = (1.25 ±0.05)
%uncertainty length (%ΔI) = 0.05 x 100 = 4%
1.25
% uncertainty T = ½ x % uncertainty l
% ΔT = ½ x % ΔI
* For measurement raised to power of n, multiply % uncertainty by n
Random and Systematic Error
T  (2.24  2%)
AbsoluteT 
2
 2.24  0.044
100
T  (2.24  0.044)
T  (2.24  0.04)
Correct value = 2.15
Expt value
= 2.24 ±2%
%Percentage Error = 4.2%
%Error  (
exp t  correct
) 100%
correct
%Error  (
2.24  2.15
) 100%  4.2%
2.15
T  (2.24  2%)
% Random Error
%Random Error = 2%
%Systematic Error = 2.2%
% error fall outside> than % uncertainty (%Random error)
• Random error cannot account for % error
• Systematic error occur – way to reduce systematic error

6. Random and Systematic Error
Measuring Area using ruler
Recording measurement using
uncertainty of equipment
Length, I = (4.52 ±0.02) cm
Height, h = (2.0 ±0.2)cm3
Treatment of Uncertainty
Multiplying or dividing measured quantities
Area, A  Length, l  height, h
% uncertainty = sum of % uncertainty of individual quantities
Length, l = (4.52 ±0.02)
%uncertainty length (%Δl) = 0.02 x 100 = 0.442%
4.52
Height, h = (2.0 ±0.2)
%uncertainty height (%Δh) = 0.2 x 100 = 10%
2.0
% uncertainty A = % uncertainty length + % uncertainty height
% ΔA =
% ΔI
+
%Δh
Random and Systematic Error
Area  4.52 2.0  9.04
0.02
100%  0.442%
4.52
0.2
%h 
100%  10%
2.0
%A  %l  %h
%A  0.442%  10%  10.442%
Area  (9.04  10%)
%l 
AbsoluteA 
10
 9.04  0.9
100
Area  (9.0  0.9)
%Percentage Error = 9%
Correct value = 22.7
Expt value
= 24.8 ±0.87%
%Error  (
Area, A  Length, l  height, h
exp t  correct
) 100%
correct
24.8  22.7
%Error  (
) 100%  9%
22.7
Area  (9.04  10%)
% Random Error
%Random Error = 10%
% error fall within the % uncertainty (%Random error)
• Little/No systematic error
• Result is reliable – need to reduce random error
Reduce random error – HUGE (10%) – use precise instrument vernier calipers
Vernier caliper

7. Random and Systematic Error
Measuring moles using
dropper and volumetric flask
Conc, c
= (2.00 ±0.02) cm
Volume, v = (2.0 ±0.1)dm3
Mole, n  Conc, c Volume, v
Mole  2.00 2.0  4.00
0.02
100%  1%
2.00
0.1
%v 
100%  5%
2.0
%n  %c  %v
%c 
Treatment of Uncertainty
Multiplying or dividing measured quantity Mole, n  Conc Vol
% uncertainty = sum of % uncertainty of individual quantity
Conc, c = (2.00 ±0.02)
%uncertainty conc (%Δc) = 0.02 x 100 = 1%
2.00
Volume, v = (2.0 ±0.1)
%uncertainty volume (%Δv) = 0.1 x 100 = 5%
2.0
% uncertainty n = % uncertainty conc + % uncertainty volume
% Δn =
% Δc
+
%Δv
Dropper, volumetric
flask
%n  1%  5%  6%
Mole  (4.00  6%)
Absoluten 
Mole  (4.00  0.24)
6
 4.00  0.24
100
Mole  (4.0  0.2)
%Percentage Error = 10%
Random and Systematic Error
Correct value = 3.63
Expt value
= 4.00 ±6%
exp t  correct
%Error  (
) 100%
correct
% Error  (
4  3.63
) 100%  10%
3.63
Mole  (4.00  6%)
% Random Error
%Random Error = 6%
%Systematic Error = 4%
% error fall outside> than % uncertainty (%Random error)
• Random error cannot account for % error
• Systematic error occur – improve on method/steps used.
Ways to reduce error
Random error (6%)
More precise instrument -pipette
Systematic error (4%)
Calibration of instrument

8. Random and Systematic Error
Density, D 
Measuring density using mass
and measuring cylinder
Mass, m = (482.63 ±1)g
Volume, v = (258 ±5)cm3
Density, D 
Mass
Volume
482.63
 1.870658
258
1
100%  0.21%
482.63
5
%V 
100%  1.93%
258
%D  %m  %V
%m 
Treatment of Uncertainty
Mass
Multiplying or dividing measured quantities Density, D  Volume
% uncertainty = sum of % uncertainty of individual quantities
Mass, m = (482.63 ±1)
%uncertainty mass (%Δm) = 1
x 100 = 0.21%
482.63
Volume, V = (258 ±5)
%uncertainty vol (%ΔV) = 5 x 100 = 1.93%
258
% uncertainty density = % uncertainty mass + % uncertainty volume
% ΔD =
% Δm
+
%ΔV
%D  0.21%  1.93%  2.1%
Density  (1.87  2.1%)
AbsoluteD 
2.1
1.87  0.04
100
Density  (1.87  0.04)
%Percentage Error = 5%
Random and Systematic Error
Correct value = 1.78
Expt value
= 1.87 ±2.1%
%Random Error = 2.1%
exp t  correct
%Error  (
) 100%
correct
1.87  1.78
%Error  (
) 100%  5%
1.78
%Systematic Error = 2.9%
% error fall outside> than % uncertainty (%Random error)
• Random error cannot account for % error
• Systematic error occurs
Ways to reduce error
Density  (1.87  2.1%)
Random error (6%)
Precise instrument
mass balance
% Random Error
Precise balance
Systematic error (4%)
Use different method like
displacement can
Displacement can

9. Random and Systematic Error
Measuring Enthalpy change using calorimeter/thermometer
Recording measurement using
uncertainty of equipment
Mass water = (2.00 ±0.02)g
ΔTemp
= (2.0 ±0.4) C
Treatment of Uncertainty
Multiplying or dividing measured quantities Enthalpy, H
% uncertainty = sum of % uncertainty of individual quantities
Mass, m = (2.00 ±0.02)
%uncertainty mass (%Δm) = 0.02 x 100 = 1%
2.00
ΔTemp = (2.0 ±0.4)
%uncertainty temp (%ΔT) = 0.4 x 100 = 20%
2.0
% uncertainty H = % uncertainty mass + % uncertainty temp
% ΔH =
% Δm
+
%ΔT
 m  c  T
Enthalpy, H  2.00 4.18 2.0  16.72
0.02
100%  1%
2.00
0.4
%T 
100%  20%
2.0
%H  %m  %T
%m 
%H  1%  20%  21%
Enthalpy  (16.72  21%)
AbsoluteH 
21
16.72  3.51
100
Enthalpy  (16.72  3.51)
Enthalpy  (17  4)
Random and Systematic Error
%Percentage Error = 50%
Correct value = 33.44
Expt value
= 16.72 ±21%
%Error  (
Enthalpy, H  m  c  T
exp t  correct
) 100%
correct
%Random Error =21%
16.72  33.44
% Error  (
) 100%  50%
33.44
Enthalpy  (16.72  21%)
%Systematic Error = 29%
% error fall outside> than % uncertainty (%Random error)
• Random error cannot account for % error
• Systematic error occurs – reduce this error
Ways to reduce error
Random error (21%)
Precise Temp sensor
% Random Error
Temp sensor
Systematic error (29%)
Reduce heat loss
using styrofoam cup

10. Random and Systematic Error
Measuring speed change using stopwatch
Recording measurement using
uncertainty of equipment
G = (20 ± 0.5)
H = (16 ± 0.5)
Z = (106 ± 1.0)
Treatment of Uncertainty
Multiplying or dividing measured quantities
Speed, s 
✔
Addition
add absolute uncertainty
Speed, s 
G+H = (36 ± 1)
Z = (106 ± 1.0)
(G  H )
Z
% uncertainty = sum of % uncertainty of individual quantities
(G + H) = (36 ±1)
%uncertainty (G+H) (%ΔG+H) = 1 x 100 = 2.77%
36
Z = (106 ±1.0)
%uncertainty Z (%Δz) = 1.0 x 100 = 0.94%
106
%uncertainty s = %uncertainty(G+H) + %uncertainty(Z)
% Δs = % Δ(G+H)
+
%Δz
(G  H )
Z
(20  16)
 0.339
106
1.0
%(G  H ) 
100%  2.77%
36
1.0
%Z 
100%  0.94%
106
Speed, s 
%S  %(G  H )  %Z
%S  2.77%  0.94%  3.7%
Speed, s  (0.339  3.7%)
AbsoluteS 
*Adding or subtracting- Max absolute uncertainty is the SUM of individual uncertainties
Random and Systematic Error
3.7
 0.339  0.012
100
Speed, s  (0.339  0.012)
%Percentage Error = 3%
Correct value = 0.330
Expt value
= 0.339 ±3.7%
%Error  (
%Error  (
exp t  correct
) 100%
correct
%Random Error = 3.7%
% error fall within the % uncertainty (%Random error)
• Little/No systematic error
• Result is reliable – need to reduce random error
0.339  0.330
) 100%  3%
0.330
Ways to reduce error
Speed  (0.339  3.7%)
Random error (3.7%)
Precise time sensor
% Random Error
precise time sensor
No systematic error
Steps/method are reliable.

11. Random and Systematic Error
Recording measurement using
uncertainty of equipment
Volt, v = (2.0 ± 0.2)
Current, I = ( 3.0 ± 0.6)
Temp, t = (4.52 ± 0.02)
Treatment of Uncertainty
Multiplying or dividing measured quantities
Energy, E 
0.02
 100%  0.442%
4.52
0 .6
% I 
 100%  20%
3 .0
0.2
% v 
 100%  10%
2.0
1
%E  %t  2  % I   %v
2
% t 
tI2
v1/ 2
% uncertainty = sum of % uncertainty of individual quantity
Time, t = (4.52 ±0.02)
%uncertainty temp (%Δt) = 0.02 x 100 = 0.442%
4.52
Current, I = (3.0 ±0.6)
%uncertainty current (%ΔI) = 0.6 x 100 = 20%
3.0
Volt, v = (2.0±0.2)
%uncertainty volt (%Δv) = 0.2 x 100 = 10%
2.0
% ΔE = %Δt + 2 x %ΔI + ½ x %ΔV
%E  
tI2
Energy, E  1/ 2
v
4.52(3.0) 2
Energy, E 
 28.638
2.01/ 2
0.02
0.6
1 0.2
100%    2  100%     100%   45%
4.52
3.0
2 2.0
Energy, E  (28.638  45%)
AbsoluteE 
Energy, E  (29  13)
45
 28.638  13
100
Random and Systematic Error
%Percentage Error = 50%
Correct value = 19.092
Expt value
= 28.638 ±45%
%Error  (
exp t  correct
) 100%
correct
%Random Error = 45%
% error fall outside> than % uncertainty (%Random error)
• Random error cannot account for % error
• Systematic error occur – small compared to random error
28.638  19.092
%Error  (
) 100%  50%
19.092
Energy, E  (28.638  45%)
% Random Error
%Systematic Error = 5%
Reduce random error – HUGE (45%)
Precise instrument.
Temp sensor

12. Expt on enthalpy change of displacement between Zinc and copper sulphate
25 ml (1M) (0.025mole) CuSO4 solution added to cup. Initial Temp, T1 taken. Excess zinc powder was added.
Final Temp T2 was taken. Calculate ΔH for reaction.
Treatment of uncertainty
Adding or subtracting
Max absolute uncertainty is the SUM of individual uncertainties
Addition/Subtraction/Multiply/Divide
Multiplying or dividing
Max %uncertainty is the SUM of individual %uncertainties
Addition/Subtraction
Add absolute uncertainty
Initial mass beaker, M1
= (20.00 ±0.01) g
Final mass beaker + CuSO4 M2 = (45.00 ±0.01)g
Mass CuSO4 m = (M2 –M1)
Absolute uncertainty, Δm = (0.01 + 0.01) = 0.02
Initial Temp, T1 = (20.0 ±0.2)C
Final Temp, T2 = (70.6 ±0.2)C
Diff Temp ΔT = (T2 –T1)
Absolute uncertainty, ΔT = (0.2 + 0.2) = 0.4
Enthalpy, H = (M2-M1) x c x (T2-T1)
Enthalpy, H  m  c  T
Multiplication
Add % uncertainty
Enthalpy, H  25.00  4.18  50.6  5.29
Mass CuSO4 m = (45.00 –20.00) = 25.00
Absolute uncertainty, Δm = (0.01 + 0.01) = 0.02
Mass CuSO4 m = (25.00 ±0.02)g
Mass CuSO4 m = (25.00 ±0.02)g
Diff Temp ΔT = (70.6 –20.0) = 50.6
Absolute uncertainty, ΔT = (0.2 + 0.2) = 0.4
Diff Temp, ΔT = (50.6 ±0.4)
ΔTemp = (50.6 ±0.4) C
Treatment of Uncertainty
Multiplying or dividing measured quantities Enthalpy, H  m  c  T
% uncertainty = sum of % uncertainty of individual quantities
Mass, m = (25.00 ±0.02)
%uncertainty mass (%Δm) = 0.02 x 100 = 0.08%
25.00
ΔTemp = (50.6 ±0.4)
%uncertainty temp (%ΔT) = 0.4 x 100 = 0.8%
50.6
% uncertainty H = % uncertainty mass + % uncertainty temp
% ΔH =
% Δm
+
%ΔT
0.025moleCuSO4  5.29
1moleCuSO4  5.29 
1
 212
0.025
0.02
 100%  0.08%
25.00
0.4
%T 
100%  0.8%
50.6
%H  %m  %T
%m 
%H  0.08%  0.8%  0.88%
Enthalpy  (212  0.88%)
AbsoluteH 
Enthalpy  (212  1.8)
Enthalpy  (212  2)
0.88
 212  1.86
100
Continue  next slide

13. Random and Systematic Error
Measuring Enthalpy change using calorimeter/thermometer
Enthalpy = (212 ± 0.88%)
Recording measurement using
uncertainty of equipment
Mass CuSO4 = (25.00 ±0.02)g
ΔTemp
= (50.6 ±0.4) C
%Percentage Error = 15%
Random and Systematic Error
Correct value = 250
Expt value
= 212 ±0.8%
%Random Error =0.88%
%Error  (
% Error  (
exp t  correct
) 100%
correct
%Systematic Error = 14.1%
% error fall outside> than % uncertainty (%Random error)
• Small random error cannot account for % error
• Systematic error occurs – reduce this error
212  250
) 100%  15%
250
Ways to reduce error
Enthalpy  (212  0.88%)
% Random Error
Reduce heat loss
use styrofoam cup
Extrapolate to higher temp
(Temp correction)
Small random error
Equipments OK
Systematic error (14.2%)
Stir the solution to
distribute heat
stirrer
•
•
•
•
Assumption wrong
Heat capacity cup is significant
Specific heat capacity CuSO4 is not 4.18
Thermometer has measurable heat capacity
Density solution not 1.00g/dm3
✗