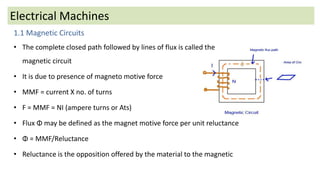
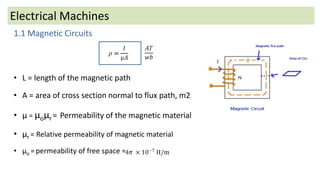
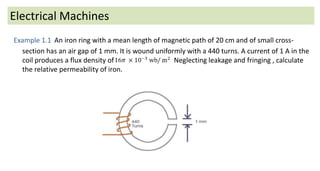
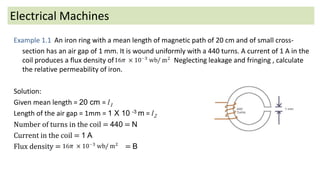
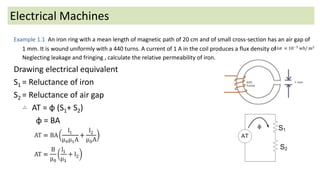
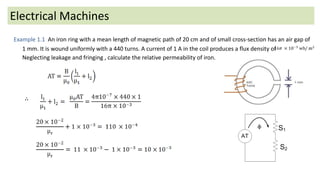
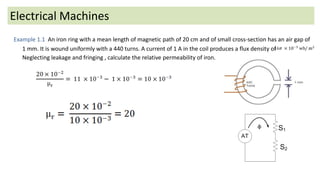
The document discusses magnetic circuits and permeability in electrical machines. It defines key terms like magnetic flux, magnetomotive force, reluctance, and permeability. It also provides an example problem calculating the relative permeability of iron in a magnetic circuit containing an iron ring with an air gap, given the geometry, current, and flux density. The example sets up the magnetic circuit equivalent and solves for the relative permeability of the iron.

1. Electrical Machines

2. Electrical Machines
1.1 Magnetic Circuits
• The complete closed path followed by lines of flux is called the
magnetic circuit
• It is due to presence of magneto motive force
• MMF = current X no. of turns
• F = MMF = NI (ampere turns or Ats)
• Flux Φ may be defined as the magnet motive force per unit reluctance
• Φ = MMF/Reluctance
• Reluctance is the opposition offered by the material to the magnetic

3. Electrical Machines
1.1 Magnetic Circuits
• L = length of the magnetic path
• A = area of cross section normal to flux path, m2
• µ = µoµr= Permeability of the magnetic material
• µr = Relative permeability of magnetic material
• µo = permeability of free space =

4. Related Videos; Click
Or Skip to Next Slide

5. Electrical Machines
Example 1.1 An iron ring with a mean length of magnetic path of 20 cm and of small cross-
section has an air gap of 1 mm. It is wound uniformly with a 440 turns. A current of 1 A in the
coil produces a flux density of . Neglecting leakage and fringing , calculate
the relative permeability of iron.

6. Electrical Machines
Example 1.1 An iron ring with a mean length of magnetic path of 20 cm and of small cross-
section has an air gap of 1 mm. It is wound uniformly with a 440 turns. A current of 1 A in the
coil produces a flux density of . Neglecting leakage and fringing , calculate
the relative permeability of iron.
Solution:
Given mean length = 20 cm = l1
Length of the air gap = 1mm = 1 X 10 -3 m = l2
Number of turns in the coil = 440 = N
Current in the coil = 1 A
Flux density = = B

7. Electrical Machines
Example 1.1 An iron ring with a mean length of magnetic path of 20 cm and of small cross-section has an air gap of
1 mm. It is wound uniformly with a 440 turns. A current of 1 A in the coil produces a flux density of
Neglecting leakage and fringing , calculate the relative permeability of iron.
Drawing electrical equivalent
S1 = Reluctance of iron
S2 = Reluctance of air gap
AT = ɸ (S1+ S2)
ɸ = BA
ɸ

8. Electrical Machines
Example 1.1 An iron ring with a mean length of magnetic path of 20 cm and of small cross-section has an air gap of
1 mm. It is wound uniformly with a 440 turns. A current of 1 A in the coil produces a flux density of
Neglecting leakage and fringing , calculate the relative permeability of iron.
ɸ

9. Electrical Machines
Example 1.1 An iron ring with a mean length of magnetic path of 20 cm and of small cross-section has an air gap of
1 mm. It is wound uniformly with a 440 turns. A current of 1 A in the coil produces a flux density of
Neglecting leakage and fringing , calculate the relative permeability of iron.
ɸ

10. Thank You
You can watch related videos by clicking on above thumbnails