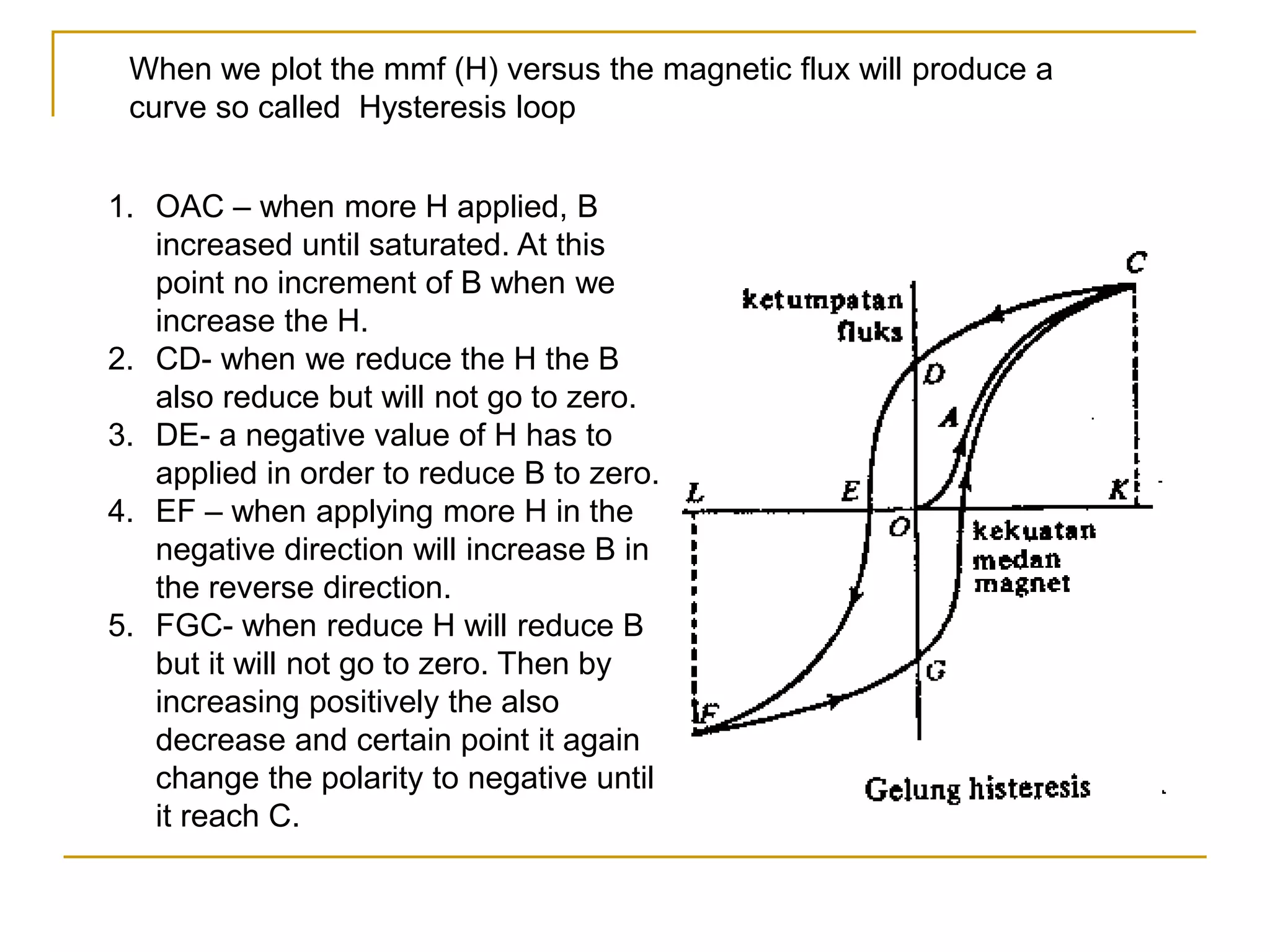
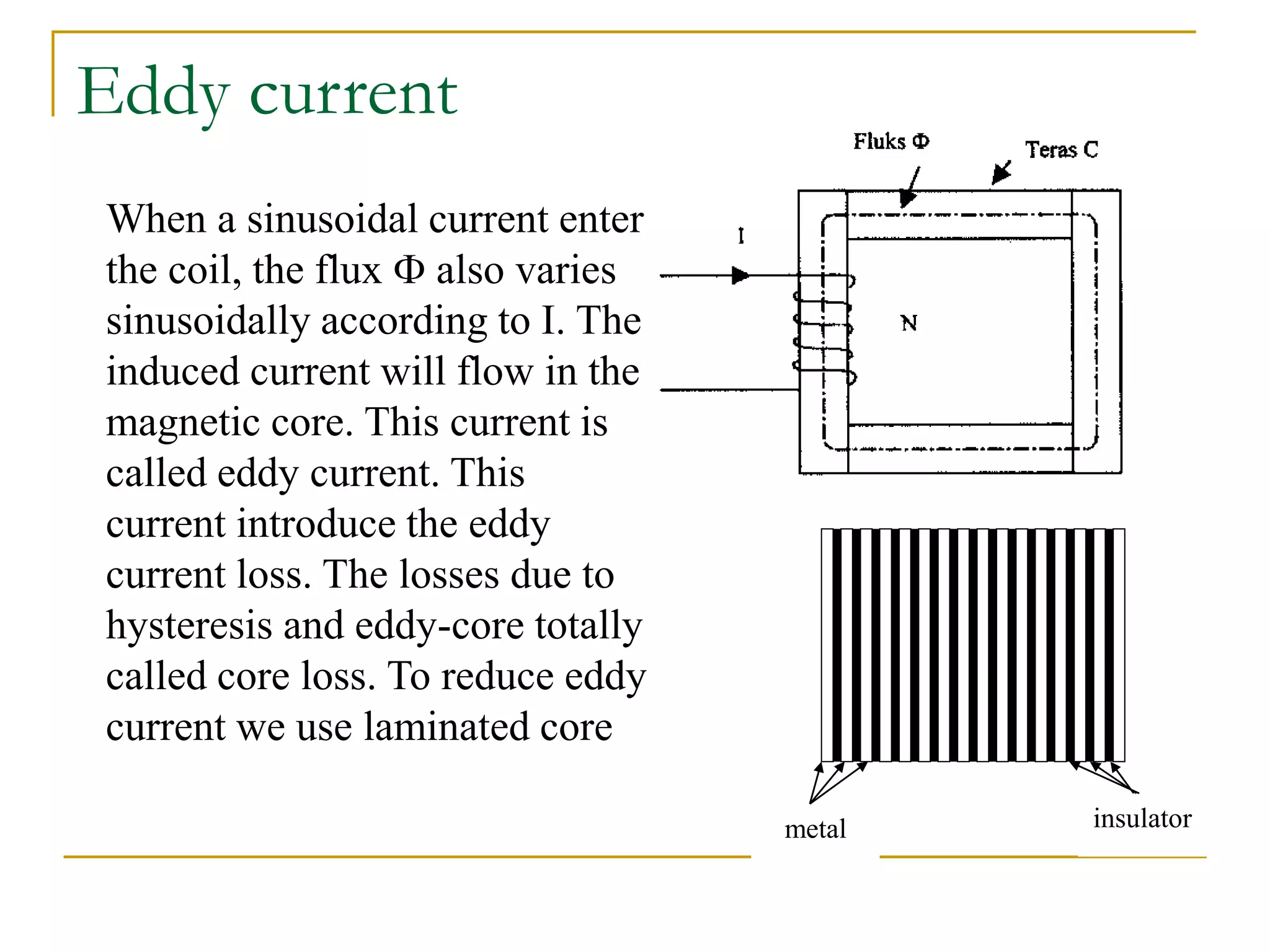
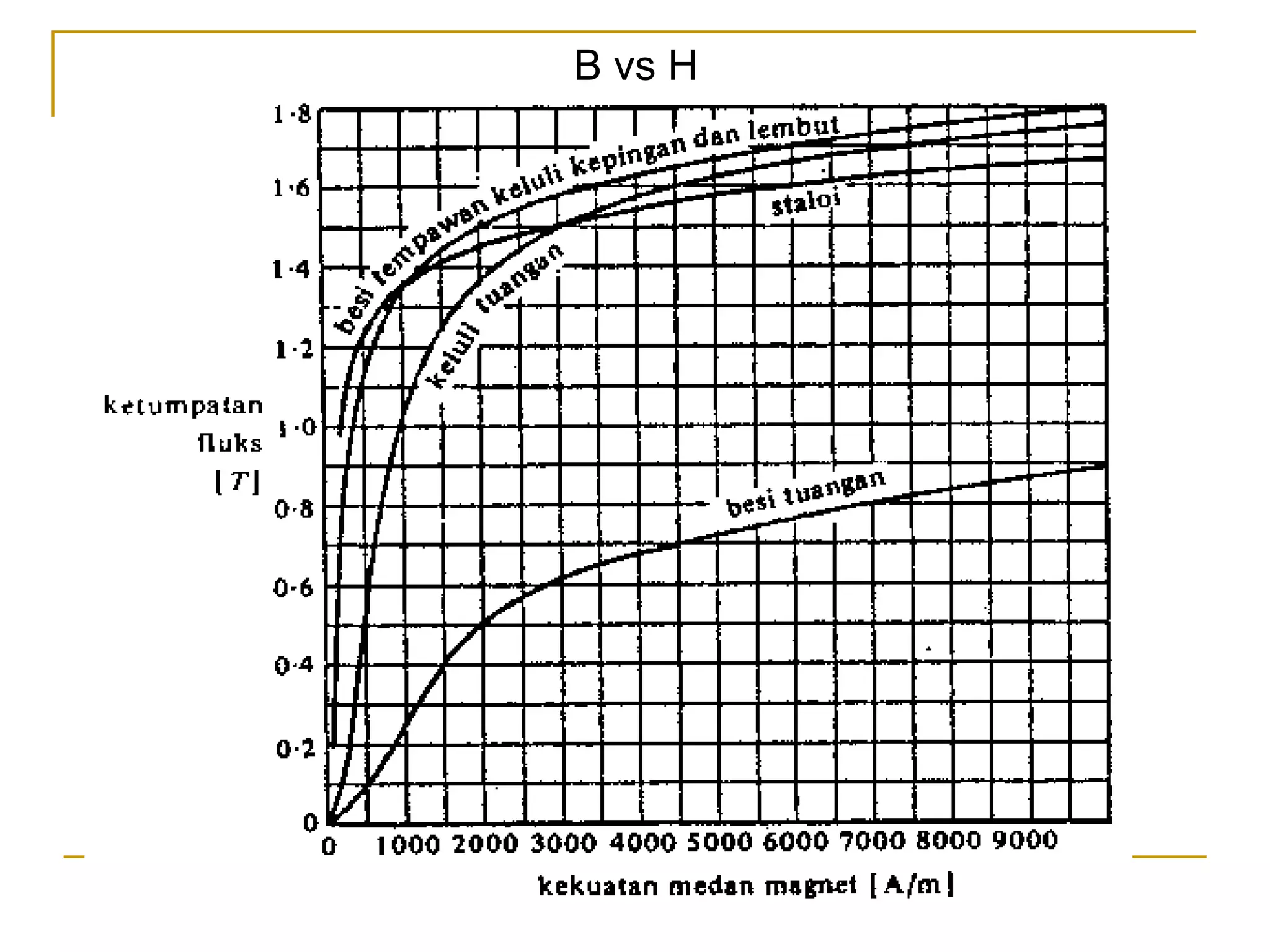
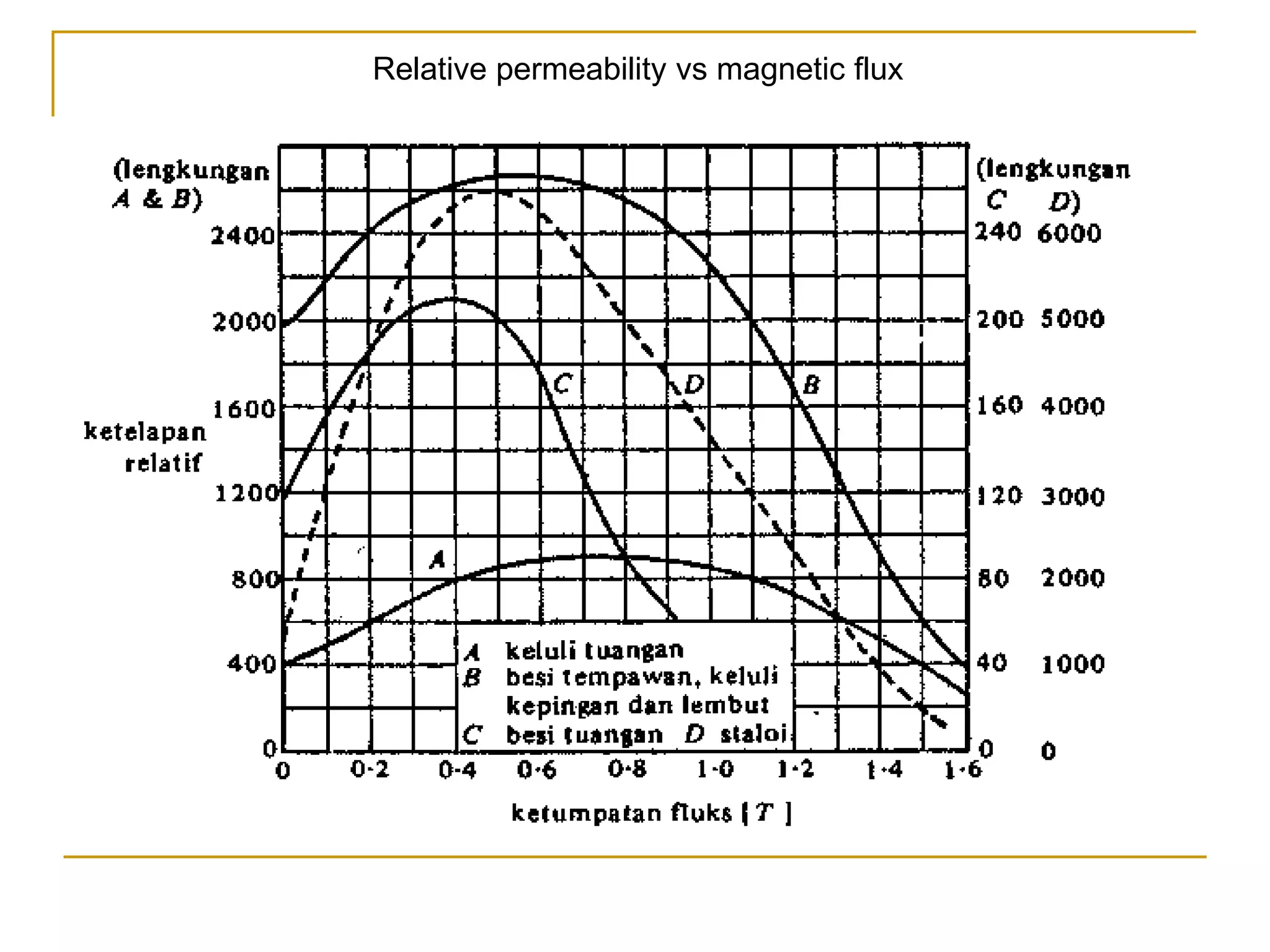
- The document discusses magnetic flux density B, magnetic flux Φ, and magnetic field strength H. It defines their units (tesla, weber, and ampere/meter respectively) and relationships between quantities. - It also discusses relative permeability and how it relates magnetic flux density B to magnetic field strength H in different materials. Lines are drawn showing trends in H and relative permeability with different materials. 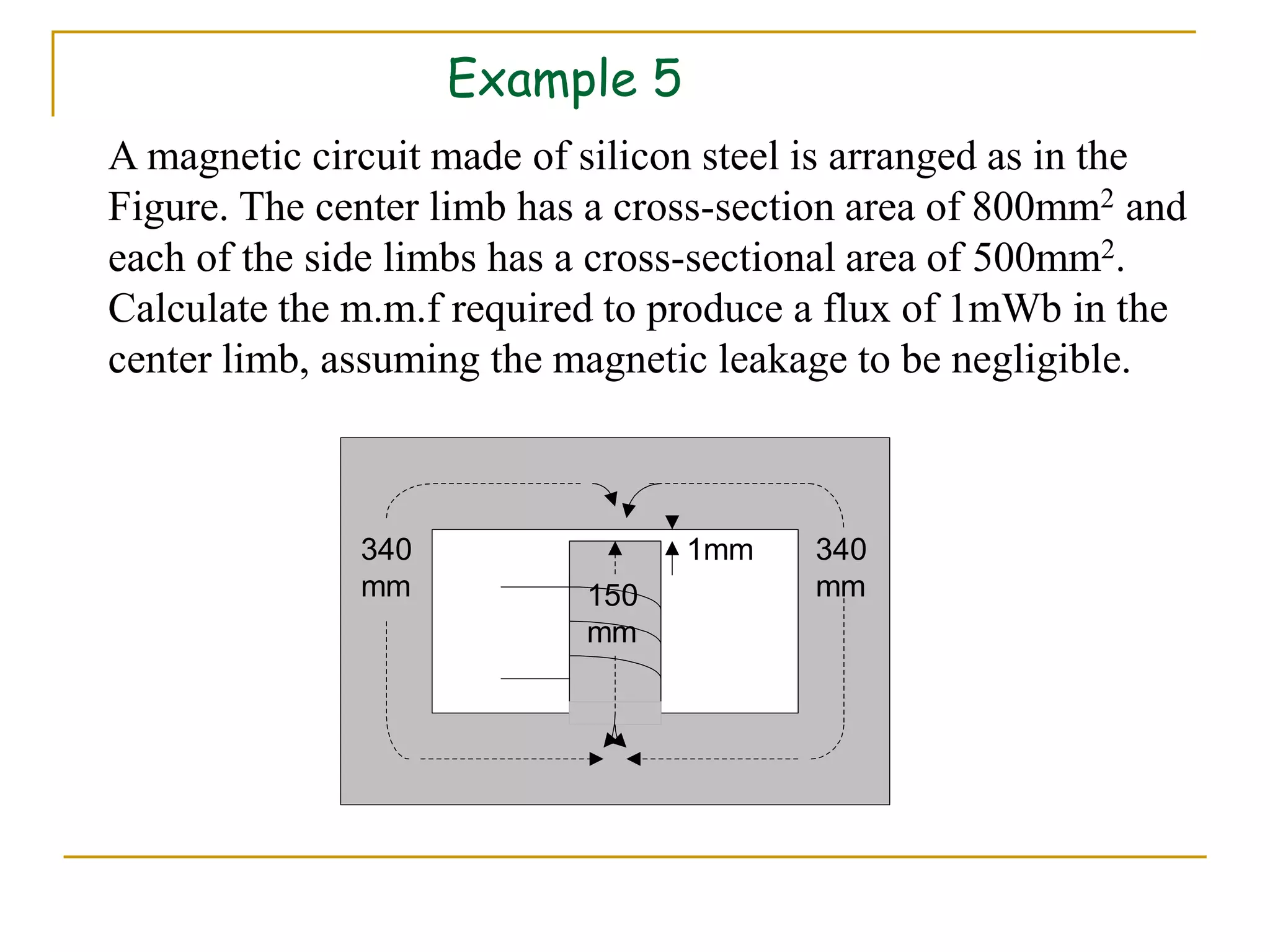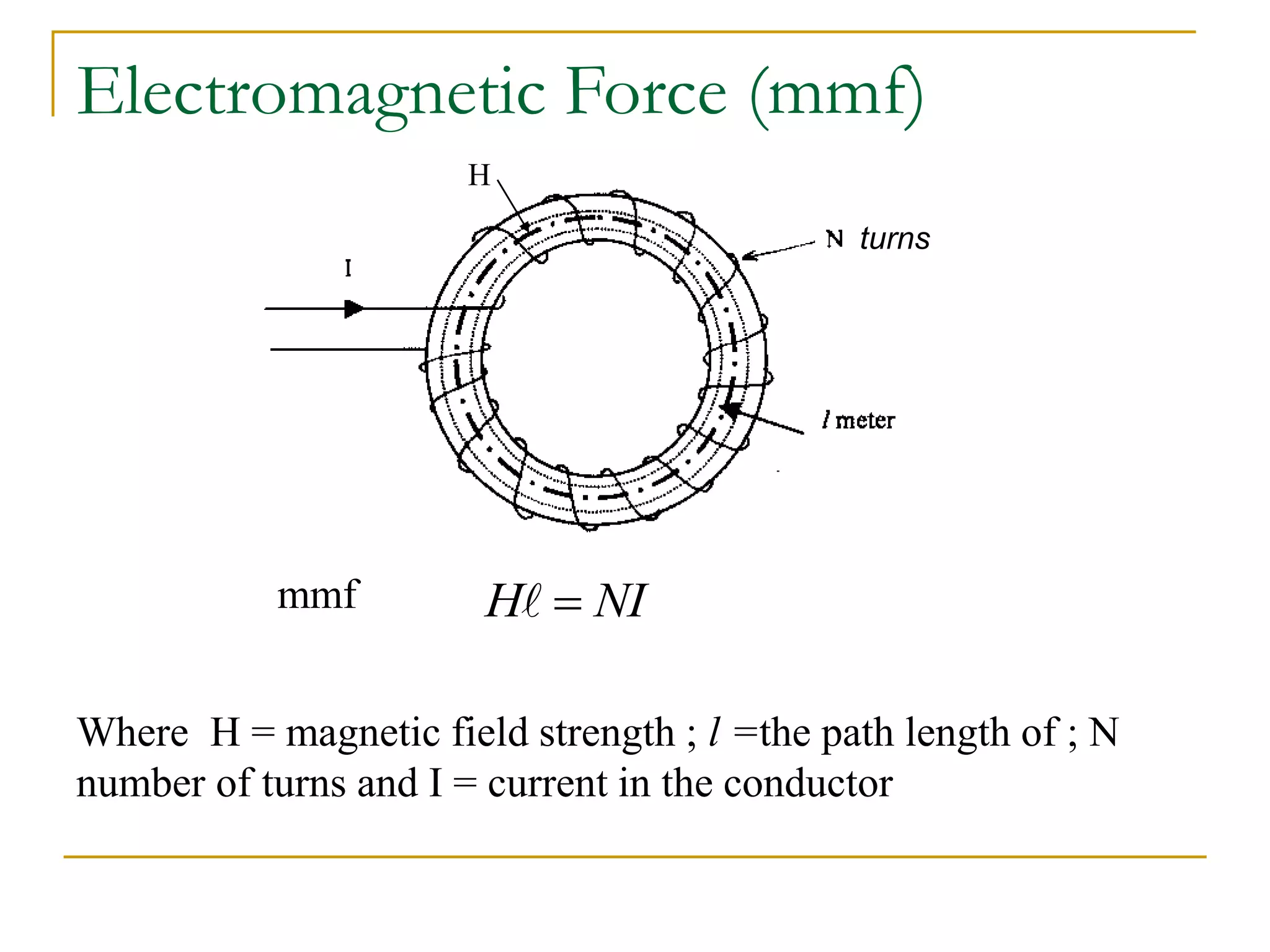- Formulas are provided relating magnetic force F, flux Φ, field strength H, and other variables. Examples are worked through applying the concepts and formulas to calculate values like flux, field strength, current, and reluctance in magnetic circuits.

2. Magnetic Flux density B
•Unit for magnetic flux density is Tesla
•The definition of 1 tesla is the flux density that
can produce a force of 1 Newton per meter acting
upon a conductor carrying 1 ampere of current.
Magnetic Flux 
•Unit for flux is weber
•The definition of 1 weber is the amount of flux
that can produce an induced voltage of 1 V in a one
turn coil if the flux reduce to zero with uniform rate.
Magnetic field strength H
•Unit for magnetic field strength is Ampere/m
•A line of force that produce flux

3. F = B l I newton
Where F = force ; B = magnetic flux density ; l =the length of
conductor and I = current in the conductor
A
B


Where  = magnetic flux ; B = magnetic flux density and A =
area of cross-section
H
B 

Where H = magnetic field strength ; B = magnetic flux density
and  = permeability of the medium
o = B/H = 4 x 10-7 H/m
Permeability in free space

4.  Relative permeability is defined as a ratio of flux density
produced in a material to the flux density produced in a
vacuum for the same magnetic filed strength. Thus
Relative Permeability (r)
r = /o
  = ro = B/H
or B = roH

5. H vs r
Relative
permeability
Magnetic field strength
Cast iron
Mild steel

6. Relative permeability vs magnetic flux

7. B vs H

8. Electromagnetic Force (mmf)
turns
H
NI
H 

mmf
Where H = magnetic field strength ; l =the path length of ; N
number of turns and I = current in the conductor

9. Example 1
A coils of 200 turns is uniformly wound around a wooden ring
with a mean circumference of 600 mm and area of cross-section
of 500 mm2. If the current flowing into the coil is 4 A, Calculate
(a) the magnetic field strength , (b) flux density dan (c) total flux
N = 200 turns
l = 600 x 10-3 m
A = 500 x 10-6 m2
I = 4 A
(a) H = NI/l = 200 x 4 / 600 x 10-3 = 1333 A
(b) B = oH = 4 x 10-7 x 1333 = 0.001675 T = 1675 T
(c) Total Flux  = BA = 1675 x 10-6 x 500 x 10-6
= 0.8375 Wb
turns

10. Ohm‘s law I = V/R [A]
Where I =current; V=voltage and R=resistance
And the resistance can be relate to physical parameters as
R =  l /A ohm
Where =resistivity [ohm-meter], l= length in meter and A=area
of cross-section [meter square]
Analogy to the ohm‘s law
V=NI=H l I= and R=S
Reluctance ( S )
 
weber
S
Hl

  
weber
ampere
A
S
o
r
/




where

11. Example 2
A mild steel ring, having a cross-section area of 500 mm2 and a
mean circumference of 400 mm is wound uniformly by a coil
of 200 turns. Calculate(a) reluctance of the ring and (b) a
current required to produce a flux of 800 Wb in the ring.
T
A
B 6
.
1
10
500
10
800
6
6





 

Dari graf r/B, pada B = 1.6;
r = 380
turns
4
7
10
5
10
4
380
4
.
0










 A
S
o
r

]
/
[
10
667
.
1 6
Wb
A


(a)

12. (b)
S
H

 S
H 


NI
A
H 




 
]
[
1342
10
667
.
1
10
800 6
6

mmf
]
[
7
.
6
200
1342
1342
A
N
I 




13. Magnetic circuit with different materials
1
1
1
A
a
S


l
2
2
2
B
a
S


l
B
A S
S
S 

2
2
2
1
1
1
a
a 



l
l
and
For A: area of cross-section = a1
mean length = l1
absolute permeability = 1
ForB: area of cross-section = a2
mean length = l2
absolute permeability = 2

14. Mmf for many materials in series
total mmf = HAlA + HBlB
HA =magnetic strength in material A
lA=mean length of material A
HB =magnetic strength in material B
lB=mean length of material B
In general
(m.m.f) = Hl

15. Example 3
A magnetic circuit comprises three parts in series, each of
uniform cross-section area(c.s.a). They are :
(a)A length of 80mm and c.s.a 50 mm2;
(b)A length of 60mm and c.s.a 90mm2;
(c)An airgap of length 0.5mm and c.s.a 150 mm2.
A coil of 4000 turns is wound on part (b), and the flux density
in the airgap is 0.3T. Assuming that all the flux passes through
the given circuit, and that the relative permeability r is 1300,
estimate the coil current to produce such a flux density.
Wb
A
B C
C
4
4
10
45
.
0
10
5
.
1
3
.
0 









16. mA
A
I 4
.
45
10
4
.
45
4000
8
.
181 3



 
At
A
S
a
o
r
a
a 1
.
44
10
50
10
4
1300
10
80
10
45
.
0
6
7
3
4











 







At
S
S
S
NI c
b
a 8
.
181
3
.
119
4
.
18
1
.
44 









and
Mmf =  S = H l = N I
At
A
S
b
o
r
b
b 4
.
18
10
90
10
4
1300
10
60
10
45
.
0
6
7
3
4











 







At
A
S
c
o
r
c
c 3
.
119
10
150
10
4
1300
10
5
.
0
10
45
.
0
6
7
3
4











 







Material a
Material b
airgap
Total mmf

17. Leakages and fringing of flux
Some fluxes are leakage via paths a, b and c . Path d is
shown to be expanded due to fringing. Thus the usable
flux is less than the total flux produced, hence
Magnetic circuit with air-gap Leakages and fringing of flux
flux
usable
flux
total
factor
Leakage 
fringing
leakage

18. Example 4
A magnetic circuit as in Figure is made
from a laminated steel. The breadth of
the steel core is 40 mm and the depth is
50 mm, 8% of it is an insulator
between the laminatings. The length
and the area of the airgap are 2 mm and
2500 mm2 respectively. A coil is
wound 800 turns. If the leakage factor
is 1.2, calculate the current required to
magnetize the steel core in order to
produce flux of 0.0025 Wb across the
airgap.

19. T
A
B
a
a 1
10
2500
10
5
.
2
6
3





 

]
/
[
796000
10
4
1
7
m
AT
B
H
o
a
a 


 


factor
leakage
airgap
in
flux
flux
Total T 



]
[
1594
002
.
0
796000 AT
H
mmf 


 
Wb
003
.
0
2
.
1
0025
.
0 


92% of the depth is laminated steel, thus the area of cross
section is
 AS = 40 x 50 x 0.92 = 1840 mm2=0.00184m

20. T
A
B
S
T
S 63
.
1
00184
.
0
10
3 3






From the B-H graph, at B=1.63T, H=4000AT/m
 mmf in the steel core = Hl = 4000 x 0.6 = 2400 AT
Total mmf. = 1592 + 2400 = 3992 AT
I = 3992/800 = 5 A
 NI = 3992

21. Mmf in loop C = NI = HLlL + HMlM
outside loop NI= HLlL + HNlN
And in loop D 0 = HMlM + HNlN
In general (m.m.f) = Hl
Magnetic circuit applying voltage law Analogy to electrical circuit
D
applying voltage Kirchoff’s law

22. L = M + N
Or L - M - N = 0
In general:  = 0
At node P we can also applying current Kirchoff’s law
P
L M N
E
Q
IL IN
IM

23. Example 5
340
mm
340
mm 150
mm
1mm
A magnetic circuit made of silicon steel is arranged as in the
Figure. The center limb has a cross-section area of 800mm2 and
each of the side limbs has a cross-sectional area of 500mm2.
Calculate the m.m.f required to produce a flux of 1mWb in the
center limb, assuming the magnetic leakage to be negligible.

24.   
a
B
A
A S
S
S
f
m
m 





 2
1
.
.
A
B

 T
A
B 25
.
1
10
800
10
1
6
3





 

15915
10
500
10
4
34000
10
340
6
7
3
1
1
1 






 




 A
S
o
r

Looking at graph at B=1.25T r =34000
Apply voltage law in loops A and B 340
mm
340
mm 150
mm
1mm
A B
4388
10
800
10
4
34000
10
150
6
7
3
2 





 



S
994718
10
800
10
4
10
1
6
7
3





 



a
S

25. 1007
999
8 


    
994718
4388
10
1
15915
10
5
.
0
.
. 3
3




 

f
m
m
Since the circuit is symmetry A =B
In the center limb , the flux is 1mWb which is equal to 2 
Therefore =0.5mWb
  
a
S
S
S
f
m
m 



 2
1 2
.
.
A

26. N
I
Weight
Iron yoke
Keeper
Air gap
Example 6
A U-shaped electromagnet shown in
Fig. is designed to lift a mass. The
material for the yoke has a relative
permeability of 2900. The yoke has a
uniform cross-sectional area of 4000
mm2 and a mean length of 600 mm.
Each of the air gaps is 0.1 mm long.
The number of turns of the coil (N) is
240. Assuming that the reluctance of
the keeper is negligible, calculate the
maximum mass in kg, which can be
lifted by the system if a current of 1.5 A
is passed through the coil. You may
neglect the fringing effect and flux
leakage; and assume that

27. a
B
a
a
o
a
a
a
a
B
B
l
B
l
H



2
10
10
4
10
1
.
0
2
2
2
3
7
3








a
a
o
r
i
a
i
i B
B
l
B
l
H



 6
.
11
10
6
10
4
2900
10
600 3
7
3







 

Calculation of maximum weight lifted by and electromagnet.
Let the flux density in the air gap be
For the air gap
For the iron yoke

28. NI
B
B
l
H
l
H
Hl a
a
i
i
a
a 











 8
.
323
10
6
.
11
6
2
1 3

T
11
.
1
8
.
323
360
8
.
323



NI
Ba
N
3922
10
4
10
4000
11
.
1
2
2 7
6
2
2
2














 



 o
a
o
a A
B
A
B
F
3922

mg
kg
400
81
.
9
3922
3922



g
m
Total mmf;
Since there are two air gaps;

29. Hysteresis loss
Materials before applying m.m.f (H), the polarity of
the molecules or structures are in random.
After applying m.m.f (H) , the polarity of the
molecules or structures are in one direction, thus the
materials become magnetized. The more H applied
the more magnetic flux (B )will be produced

30. When we plot the mmf (H) versus the magnetic flux will produce a
curve so called Hysteresis loop
1. OAC – when more H applied, B
increased until saturated. At this
point no increment of B when we
increase the H.
2. CD- when we reduce the H the B
also reduce but will not go to zero.
3. DE- a negative value of H has to
applied in order to reduce B to zero.
4. EF – when applying more H in the
negative direction will increase B in
the reverse direction.
5. FGC- when reduce H will reduce B
but it will not go to zero. Then by
increasing positively the also
decrease and certain point it again
change the polarity to negative until
it reach C.

31. Eddy current
metal insulator
When a sinusoidal current enter
the coil, the flux  also varies
sinusoidally according to I. The
induced current will flow in the
magnetic core. This current is
called eddy current. This
current introduce the eddy
current loss. The losses due to
hysteresis and eddy-core totally
called core loss. To reduce eddy
current we use laminated core