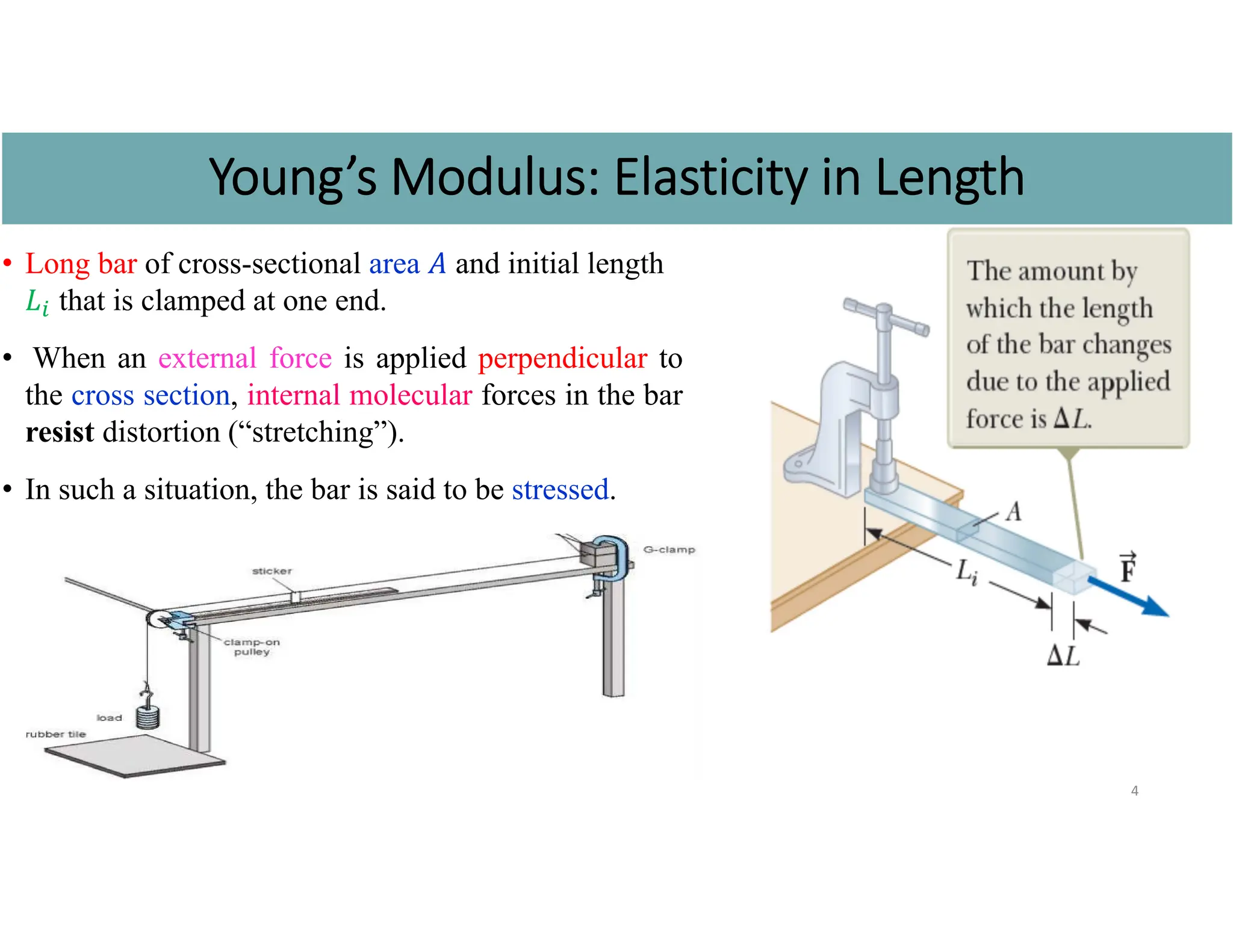
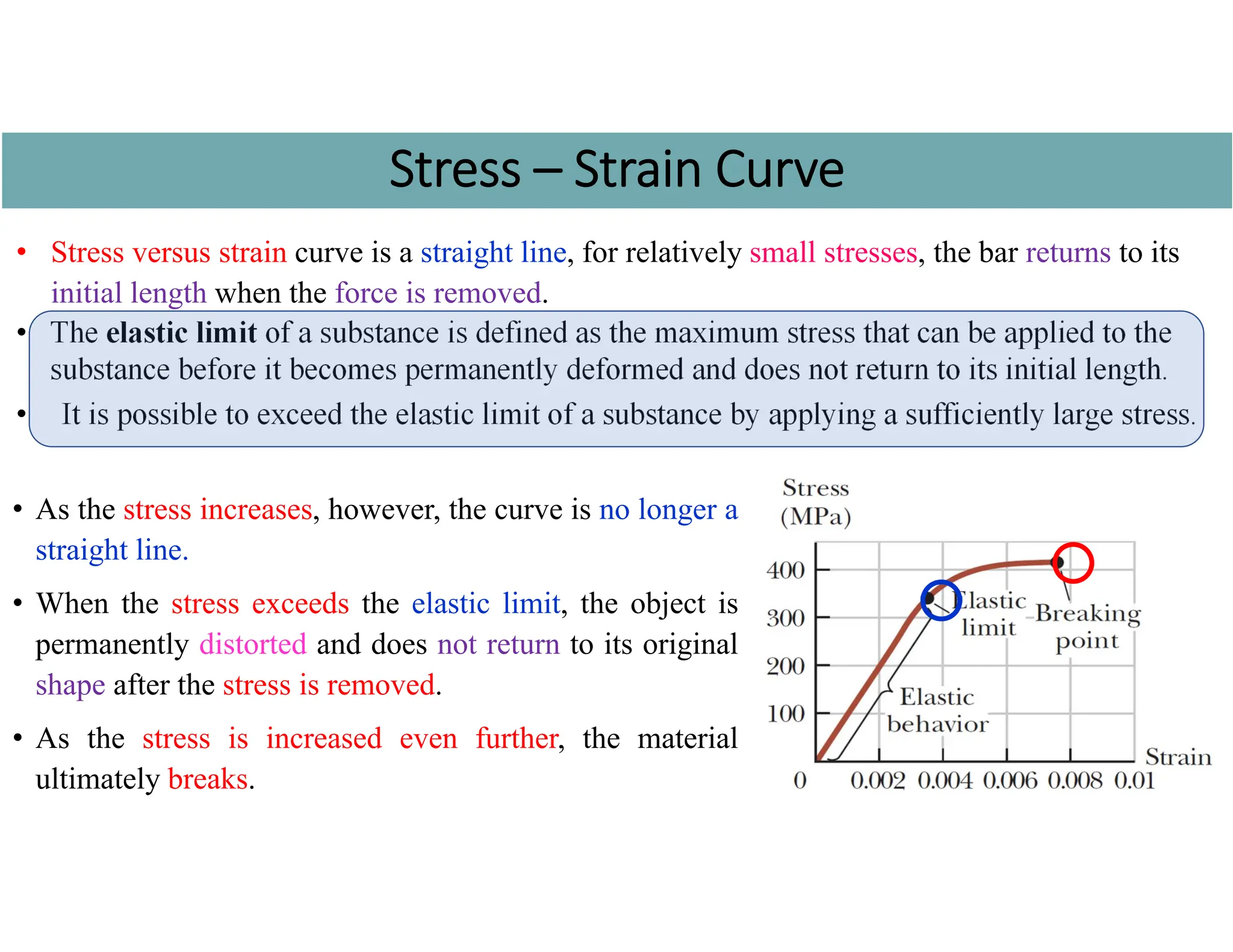
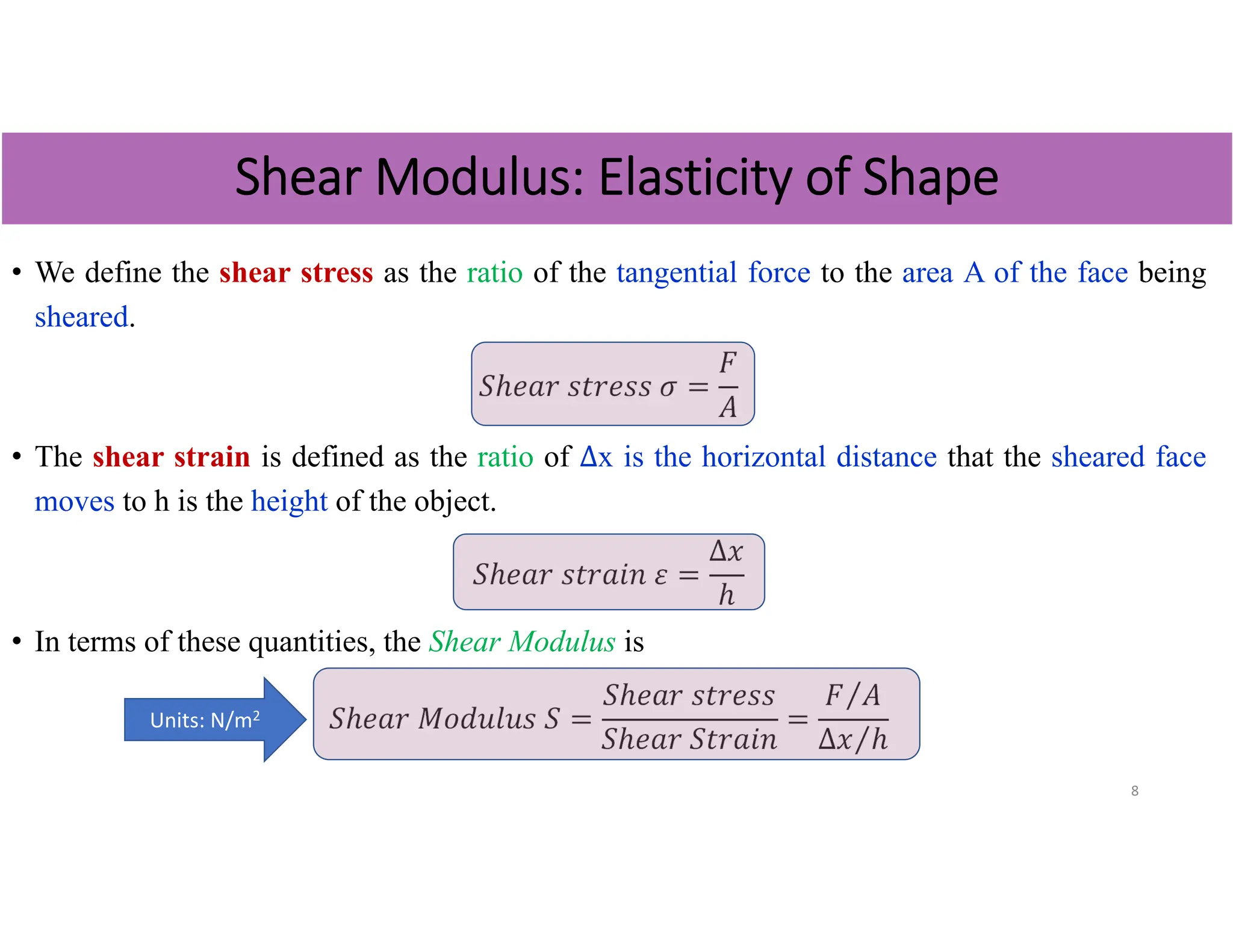
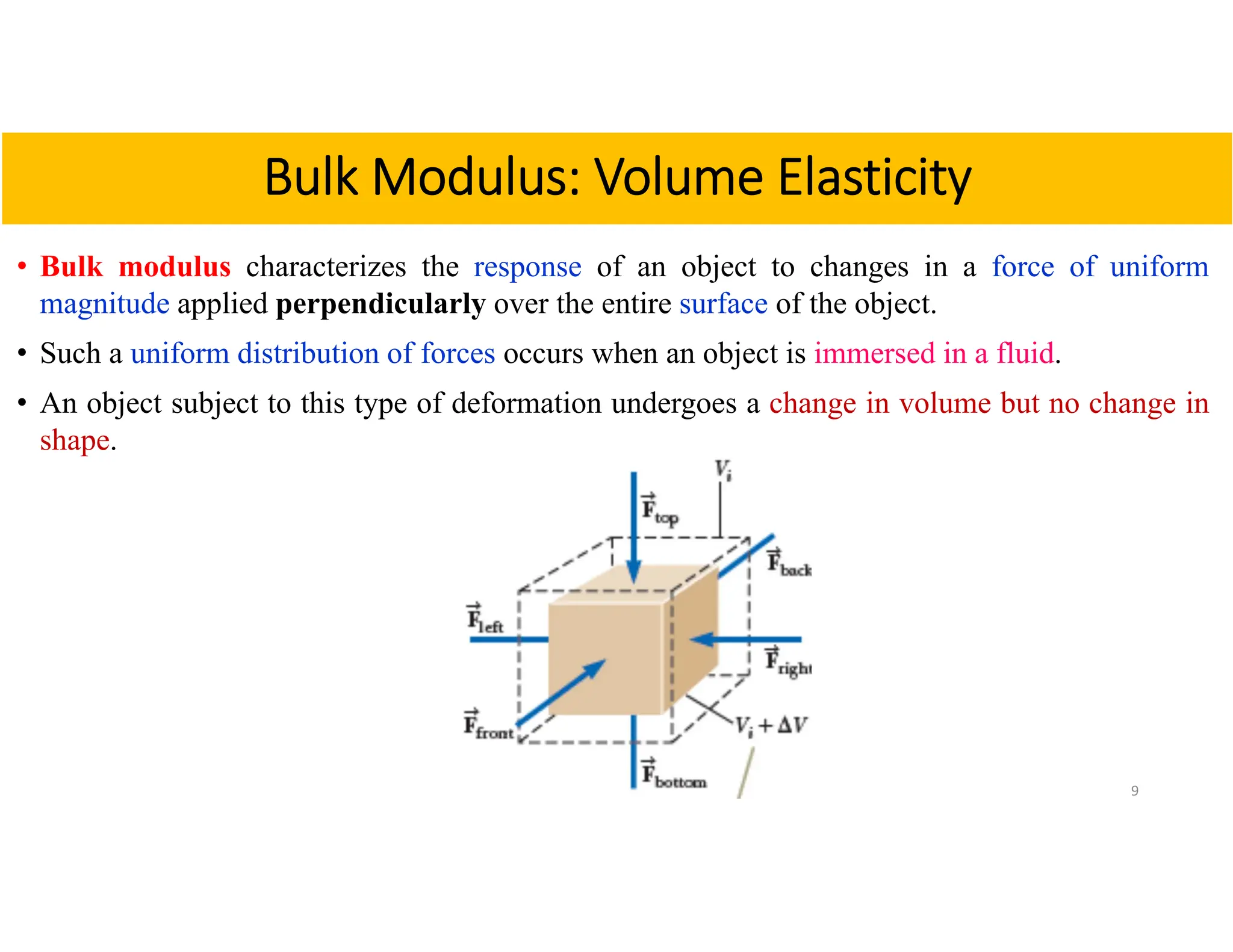
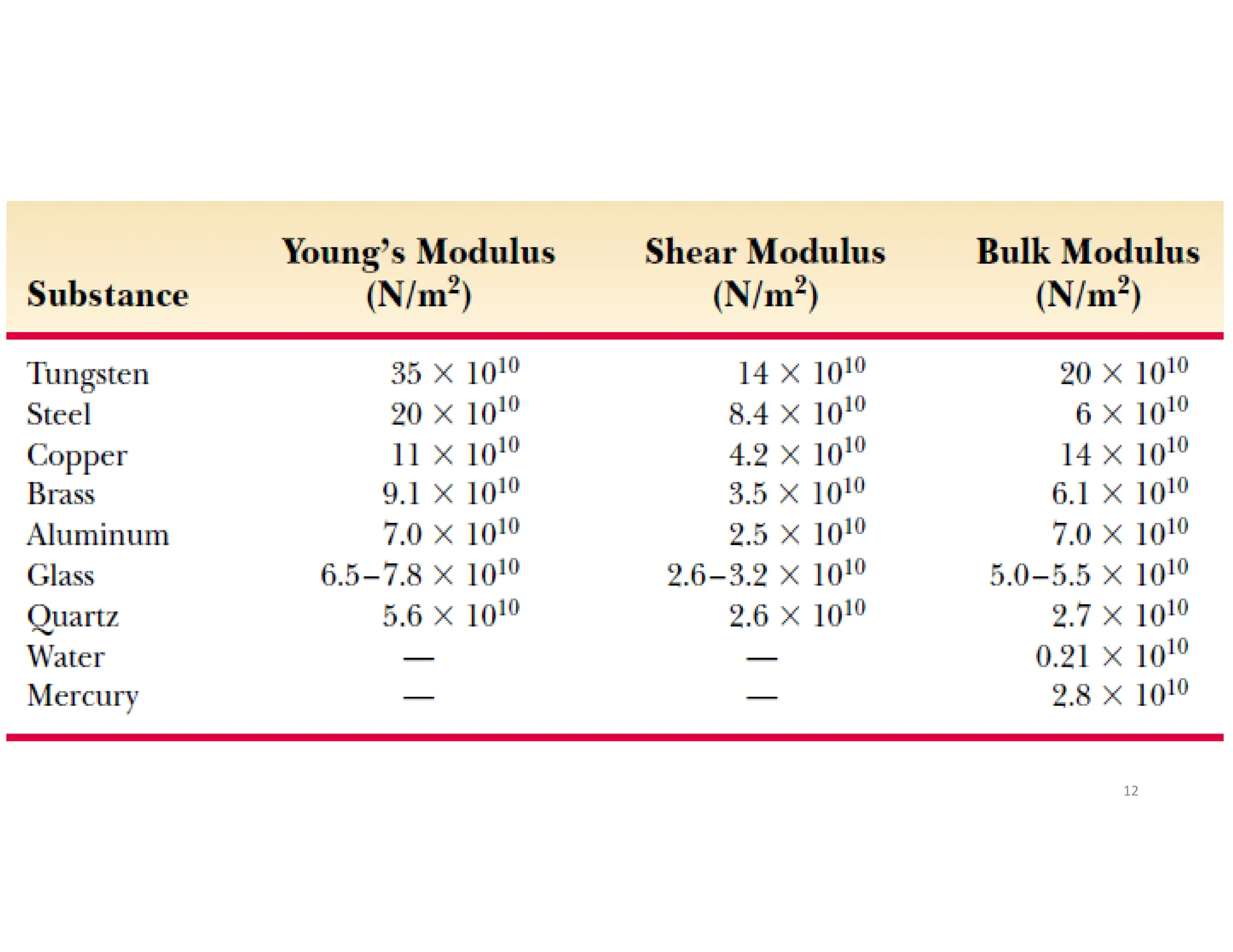
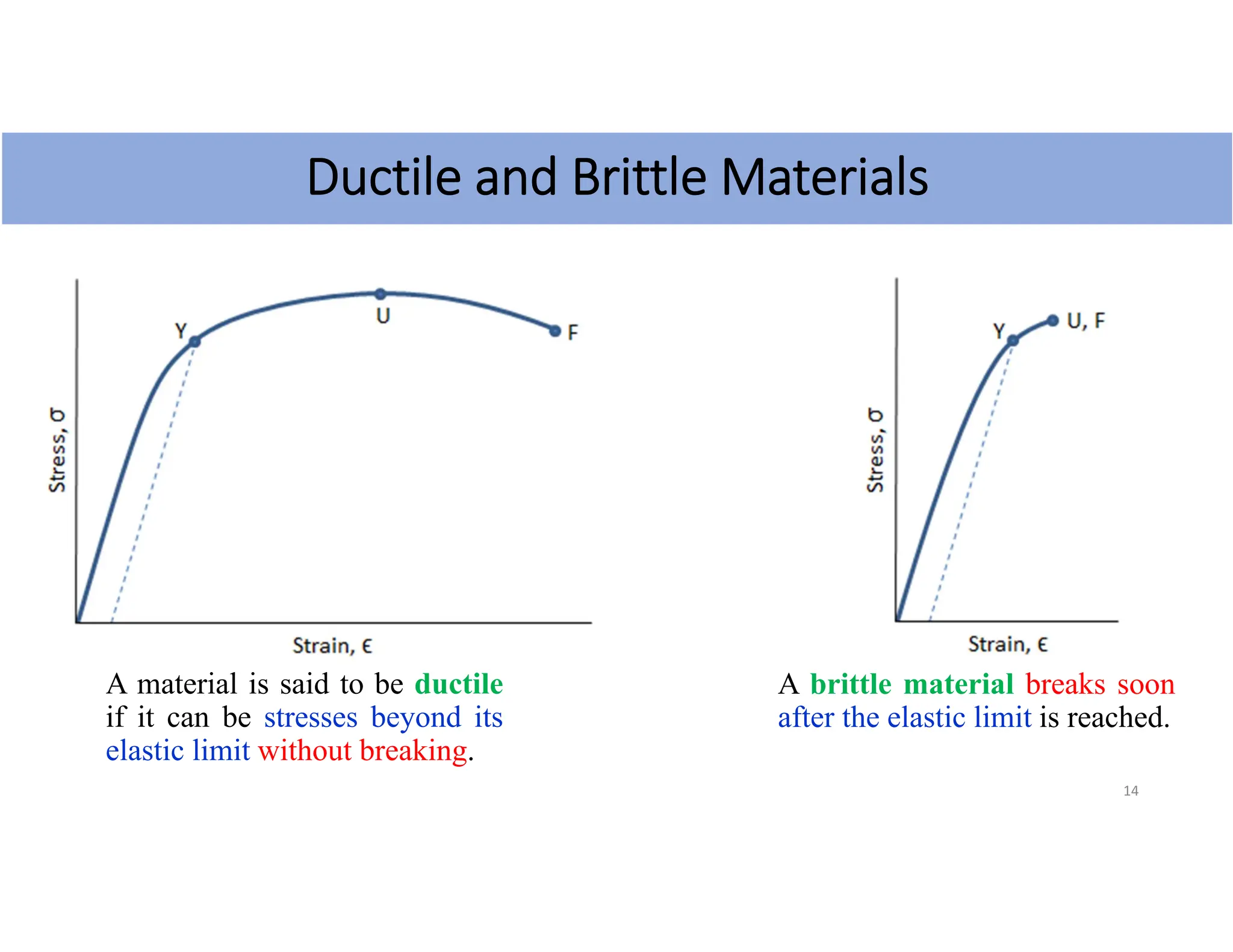
Chapter 2 focuses on the mechanical properties of materials, detailing the concepts of stress, strain, and elastic modulus, including Young's modulus, shear modulus, and bulk modulus for evaluating deformation in solids and liquids. It explains how objects deform under external forces and introduces key definitions and equations related to tensile, shear, and volume stresses. The chapter also discusses the behavior of materials, distinguishing between ductile and brittle materials and providing example calculations for practical applications.