This document contains a 35-page exam on electrical circuit analysis techniques including nodal analysis, mesh analysis, Thevenin's theorem, Norton's theorem, and maximum power transfer theorem. It includes 37 practice problems of varying difficulty, asking students to use these analysis methods to solve circuits, determine equivalent circuits, calculate voltages, currents, power, and efficiency. The document provides circuit diagrams, explanations of analysis steps, and spaces for students to show their work and solutions.

1. Page1of35(AZ)
BANGLADESH UNIVERSITY OF TEXTILES
TEJGAON, DHAKA-1208
B.Sc. in Textile Engineering
Electrical and Electronic Engineering
EEE-2
 Method of Analysis
 Network Theorem
Date: 19/02/2017

2. Page2of35(AZ)
Question
1.2) Write down the necessary steps of nodal analysis and mesh analysis. What is supernode and supermesh?
Explain with example.
2.2) State and explain superposition principle. Explain with example.
3.2) State and explain source transformation theorem. Explain with example.
4.2) How can you thevenize of a given circuit. Explain with example.
5.2) How can you nortonize of a given circuit. Explain with example.
6.2) State and prove maximum power transfer theorem. Explain with example.

3. Page3of35(AZ)
Problem
7.2) Determine the voltages at the nodes in Fig. 3.5(a)
Fig.3.5(a)
Solution:
Fig.3.5(b)

4. Page4of35(AZ)

5. Page5of35(AZ)
8.2) Find the voltages at the three nonreference nodes in the circuit of Fig. 3.6. [ v1=32 V, v2=25.6 V, v3=
62.4V ]
Fig.3.6
Answer: [Try to solve it]

6. Page6of35(AZ)
9.2) For the circuit shown in Fig, find the node voltages.
Answer: [Try to solve]
10.2) For the circuit shown in Fig. 3.9, find the node voltages.
Fig.3.9
Solution:
3.10(a)

7. Page7of35(AZ)
3.10(b)

8. Page8of35(AZ)
11.2) Find v and i in the circuit of Figure. [Answer: - 400 mV, 2.8 A]
Solution: [Try to solve]
12.2) Use mesh analysis to determine and in Fig. 3.25. [ Answer: i1=4.632 A, i2= 631.6 mA, i3=1.4736 A.]
Fig.3.25
Solution: [Try to solve]

9. Page9of35(AZ)
13.2) For the circuit in Fig. 3.18, find the branch currents I1, I2 and I3 using mesh analysis.
Fig.3.18
Solution:

10. Page10of35(AZ)
14.2) Calculate the mesh currents I1 and I2 of the circuit of Fig. 3.19. [I1=2.5A, I2=0]
Fig.3.19
Solution: [Try to solve]
15.2) Use mesh analysis to find the current Io in the circuit of Fig. 3.20.
Fig.3.20

11. Page11of35(AZ)

12. Page12of35(AZ)
16.2) Using mesh analysis, find Io in the circuit of Figure. [Answer: -4A]
Solution: [Try to solve]

13. Page13of35(AZ)
17.2) Find io and vo in the circuit of Figure.
Solution:

14. Page14of35(AZ)
18.2) For the bridge network in Figure, find io using mesh analysis.
Solution:

15. Page15of35(AZ)
19.2) Use mesh analysis to find vab and io in the circuit of the circuit.
Solution:

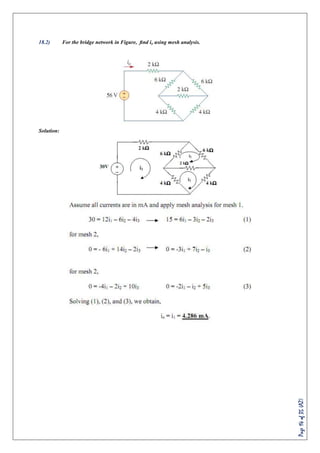
16. Page16of35(AZ)
20.2) Find vx and ix in the circuit shown in Fig.
Solution:
21.2) Determine current in 5Ω resistor by any one method. [Answer: 3.633A ]
Solution: [Try to solve]

17. Page17of35(AZ)
22.2) Apply nodal analysis to find io and the power dissipated in each resistor in the circuit .
Solution:

18. Page18of35(AZ)
23.2) Use nodal analysis to determine the voltage across 5Ω resistance and the current in the 12V
source. [Answer: 14.18 volt, 1.412 amp ]
Solution: [Try to solve]
24.2) Use the superposition theorem to find v in the circuit of Fig. 4.6.
Fig.4.6
Solution:

19. Page19of35(AZ)

20. Page20of35(AZ)
25.2) For the circuit in Fig. 4.12, use the superposition theorem to find i.
Fig.4.12
Solution:

21. Page21of35(AZ)
26.2) Find I in the circuit of Fig. 4.14 using the superposition principle. [Answer: 375 mA]

22. Page22of35(AZ)
27.2) In the circuit of Fig. 2.19 (b), find current through 1Ω resistor using both THEVENIN’s theorem
and SUPERPOSITION theorem.
2.19(b)
Solution:

23. Page23of35(AZ)

24. Page24of35(AZ)
28.2) Use source transformation to find in the circuit of Fig. 4.17.
Fig.4.17
Solution:

25. Page25of35(AZ)
29.2) Find io in the circuit using source transformation. [Answer: 1.78 A.]
30.2) Find the Thevenin equivalent circuit of the circuit shown in Fig. 4.27, to the left of the terminals a-
b Then find the current through RL= 6, 16 and 36 Ohm.
Fig.4.27
Solution:

26. Page26of35(AZ)

27. Page27of35(AZ)
31.2) Find the Thevenin equivalent of the circuit in Fig. 4.31 at terminals a-b.
Fig.4.31
Solution:

28. Page28of35(AZ)
32.2) Using Norton’s theorem, find RN and IN of the circuit in Fig. 4.43 at terminals a-b.
Fig.4.43
Solution:

29. Page29of35(AZ)

30. Page30of35(AZ)
33.2) Using Norton’s theorem, calculate the current in the 6Ω resistor in the network of as shown in
Figure. All resistance are in ohms.
Solution:
Short Circuit Current (ISC):
(a) (b)
When the branch containing 6Ω resistance is short-circuited, the given circuit is reduced to that shown in
Fig.(a) and finally to Fig. (b). As seen, the 12A current divides into two unequal parts at point A. The current
passing through 4 Ω resistor forms the short-circuit current ISC.
Norton’s Resistance (RN):
(c)
Resistance RN between points C and D when they are open-circuited. It is so because the constant-current
source has infinite resistance i.e., it behaves like an open circuit as shown in Fig.(c).
RN=(8+4)‖(10+2)=6Ω

31. Page31of35(AZ)
Norton’s Equivalent Circuit:
(d)
Hence, Norton’s equivalent circuit is as shown in Fig.(d). As seen current of 8A is divided equally between the
two equal resistances of 6Ω each. Hence, current through the required 6 Ω resistor is 4A.
Answer: Current through the required 6 Ω resistor is 4A.

32. Page32of35(AZ)
34.2) Find the value of RL for maximum power transfer in the circuit of Fig. 4.50. Find the maximum
power.
Fig.4.50
Solution:

33. Page33of35(AZ)
35.2) In the circuit shown in Fig. 2.232(a) obtain the condition from maximum power transfer to the
load RL. Hence determine the maximum power transferred.
Fig.2.232(a)
Solution:
Fig.2.232

34. Page34of35(AZ)
36.2) Prove that under maximum power transfer conditions, the power transfer efficiency is only 50%.
Power Transfer Efficiency:

35. Page35of35(AZ)
37.2) A voltage source delivers 4A when the load connected to it is 5Ω and 2A when the load becomes
20Ω. Calculate (a) maximum power which the source can supply (b) power transfer efficiency of the
source with RL of 20 Ω (c) the power transfer efficiency when the source delivers 60W.
Solution: