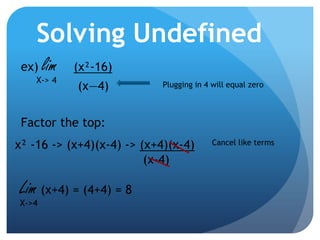
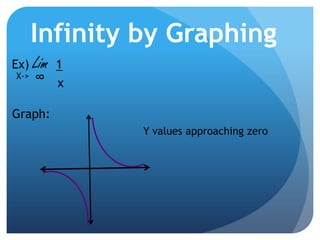
The document defines limits and discusses different methods for solving limits as the variable approaches a number or infinity. It introduces limit notation and explains how to solve limits by substitution, using sum and product laws, and handling undefined and zero cases. When taking a limit as the variable approaches infinity, it provides approaches such as determining the limit based on the highest polynomial term, and whether the numerator or denominator increases faster for rational functions.

1. LimitsBy Kathleen Hook

2. Limit DefinitionNotation: limf(x)=LX -> aThe Range (Y) Values the function is approaching as the domain (X) values get closer to a

3. Solving LimitsWhen x -> a number Plug the number into the functionLim x -> Lim (a) X-> aX-> a

4. Solving limitsEx) lim (3x) =X-> 4Substitute the number:lim 3(4) = 12X-> 4

5. Sum LawLimit of sum = sum of limitsex) lim(x²+2x-5) =X->2lim x² + lim 2x – lim5 =X->2X->2X->2(2)²+ 2(2) -5 = 3

6. Product LawLimit of product = product of limitsEx) Lim(X+6)(X-4) =X-> 2lim(x+6) lim (x-4) = X-> 2X-> 2(2+6) (2-4) = (8) (-2) = -16

7. Quotient LawLimit of quotient = quotient of limits Ex) lim(x+1) =(x-2)X-> 4Lim (x+1)=(4+1) = 5(4-2) 2X-> 4_________________Lim (x-2)X-> 4

8. Solving Limits whenSubstituting makes the function undefined Undefined: When the bottom is zeroSolve to eliminate like terms

9. Solving Undefinedex) lim (x²-16) (x—4) X-> 4Plugging in 4 will equal zeroFactor the top:x² -16 -> (x+4)(x-4) -> (x+4)(x-4) (x-4) Cancel like termsLim (x+4) = (4+4) = 8X->4

10. Numerator equals zeroThe limit is still definedEx) lim(x-6) = (8-x) X-> 6(6-6) = 0 = 0(8-x) 2

11. Solving LimitsWhen X approaches infinityNotation: lim f(x)8x -> There are multiple approaches

12. Infinity by GraphingEx) Lim1x8X-> Graph: Y values approaching zero

13. Limit by PlottingEx) Lim 1 x*already found the limit is ZeroX->8Proof: X f(X)1 15 1/5F(x) values approaching zero100 1/1001000 1/1000

14. Infinity New WayPolynomial Functions: Determined by highest power Even:Ex) limx² = …. = +InfinityOdd:Ex) lim5-3x= … = -Infinity

15. Rational FunctionsDenominator increase faster lim=0Ex) lim1 = 0 5xEx) lim3x= 0 x²+1

16. Rational FunctionsNumerator increases faster lim = -or888Ex) 4x-8x² = - 2x-1EX) x²+2x = x+98If Powers Even: ex) lim4x+1= 43x-8 3