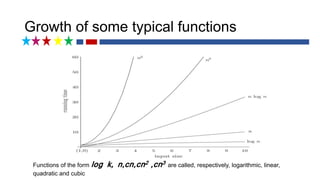
An algorithm is a sequence of unambiguous instructions to solve a problem and obtain an output for any input in a finite time. Euclid developed one of the earliest algorithms to find the greatest common divisor in 300 BC. Performance of an algorithm is evaluated based on time and space complexity. Time complexity measures the total time required and is classified based on functions like constant, logarithmic, linear, quadratic or cubic. Space complexity measures the memory required excluding input space.

1. Module I
Introduction to Algorithm

2. What is an Algorithm?
• An algorithm is a sequence of unambiguous instructions for
solving a problem, i.e., for obtaining a required output for any
legitimate input in a finite amount of time.

3. HISTORICAL PERSPECTIVE
• Euclid’s algorithm for finding the greatest common
divisor
• One of the oldest algorithms known (300 BC)
• Muhammad ibn Musa al-Khwarizmi – 9th century
mathematician
• Al-Khwarizmi principle states that all complex
problems of science must be and can be solved by
means of five simple steps

4. Notion of Algorithm
Algorithmic solution
“Computer”
input output
proble
m
algorithm

5. Example: Sorting
• Statement of problem:
• Input:
• A Sequence of n numbers < a1 , a2,a3 …….,a4 >
• Output:
• A reordering of n numbers < b1, b2 ,b3, ….bn >
• So that 𝑏𝑖 ≤ 𝑏𝑗 ,whenever i ≤ j

6. Example:
“Computer”
input output
proble
m
algorithm
Algorithmic solution
Sorting Algorithm
• Selection Sort ?
• Insertion Sort ?
• Merge Sort ?
• ….
< 5, 3, 2, 1, 8, 6 > < 1, 2, 3, 5, 6, 8
>

7. Performance Analysis of an algorithm
• Performance of an algorithm is a process of making evaluative
judgement about algorithms.
• Performance of an algorithm means predicting the resources which
are required to an algorithm to perform its task.

8. Performance Analysis (cont.)
• An algorithm is said to be efficient and fast, if it takes less time
to execute and consumes less memory space. The
performance of an algorithm is measured on the basis of
following properties :
• 1. Time Complexity
• 2. Space Complexity

9. Growth of some typical functions
Functions of the form log k, n,cn,cn2 ,cn3 are called, respectively, logarithmic, linear,
quadratic and cubic

10. Three Asymptotic Notation
• The O-notation , O(n2) (read “Oh of n2 ”or “big-Oh of n2 ”)
• The Ω-notation, Ω(n) (read “omega of n”, or “big-omega of n”)
• The Θ-notation , Θ(n2) (read “theta of n2 ”)

11. The O-notation
• In general, we say that the running time of an algorithm is O(g(n)), if
whenever the input size is equal to or exceeds some threshold n0 , its
running time can be bounded above by some positive constant c times g(n).
• Definition: Let f(n) and g(n) be two functions from the set of natural
numbers to the set of nonnegative real numbers. f(n) is said to be O(g(n)) if
there exists a natural number n0 and a constant c > 0 such that
∀ n ≥ n0 , f(n) ≤ cg(n).
Consequently, if lim
𝑛→∞
𝑓(𝑛)
𝑔(𝑛)
exists, then
if lim
𝑛→∞
𝑓(𝑛)
𝑔(𝑛)
≠ ∞ implies f(n) = O(g(n)).

12. TIME COMPLEXITY
• The time complexity of an algorithm is the total amount of time
required by an algorithm to complete its execution.
• If any program requires fixed amount of time for all input values then
its time complexity is said to be Constant Time Complexity
int sum(int a, int b)
{
return a+b;
}

13. SPACE COMPLEXITY
• We define the space used by an algorithm to be the number of
memory cells (or words) needed to carry out the computational
steps required to solve an instance of the problem excluding the
space allocated to hold the input.
• All definitions of order of growth and asymptotic bounds
pertaining to time complexity carry over to space complexity. It
is clear that the work space cannot exceed the running time of
an algorithm, as writing into each memory cell requires at least
a constant amount of time.