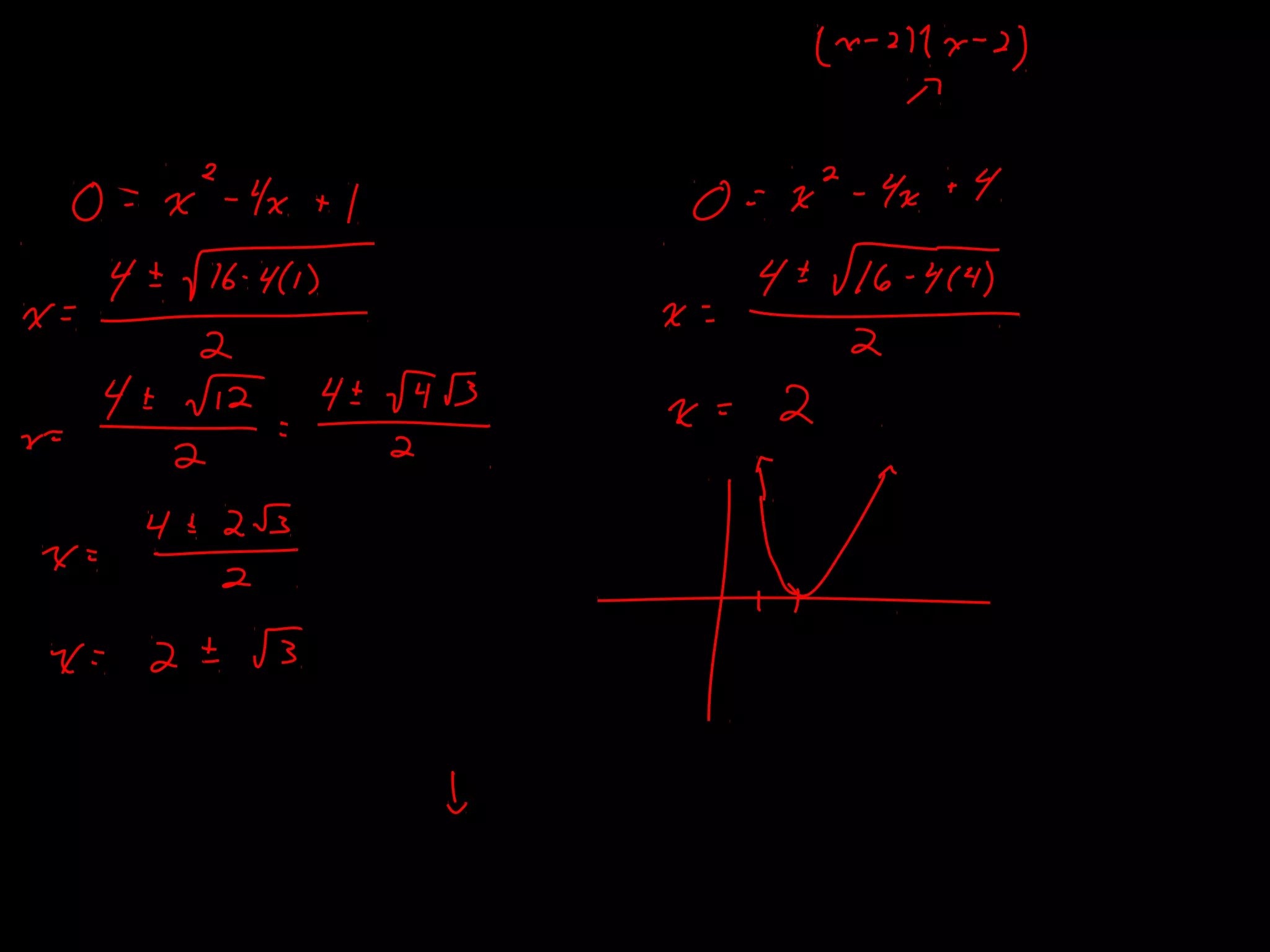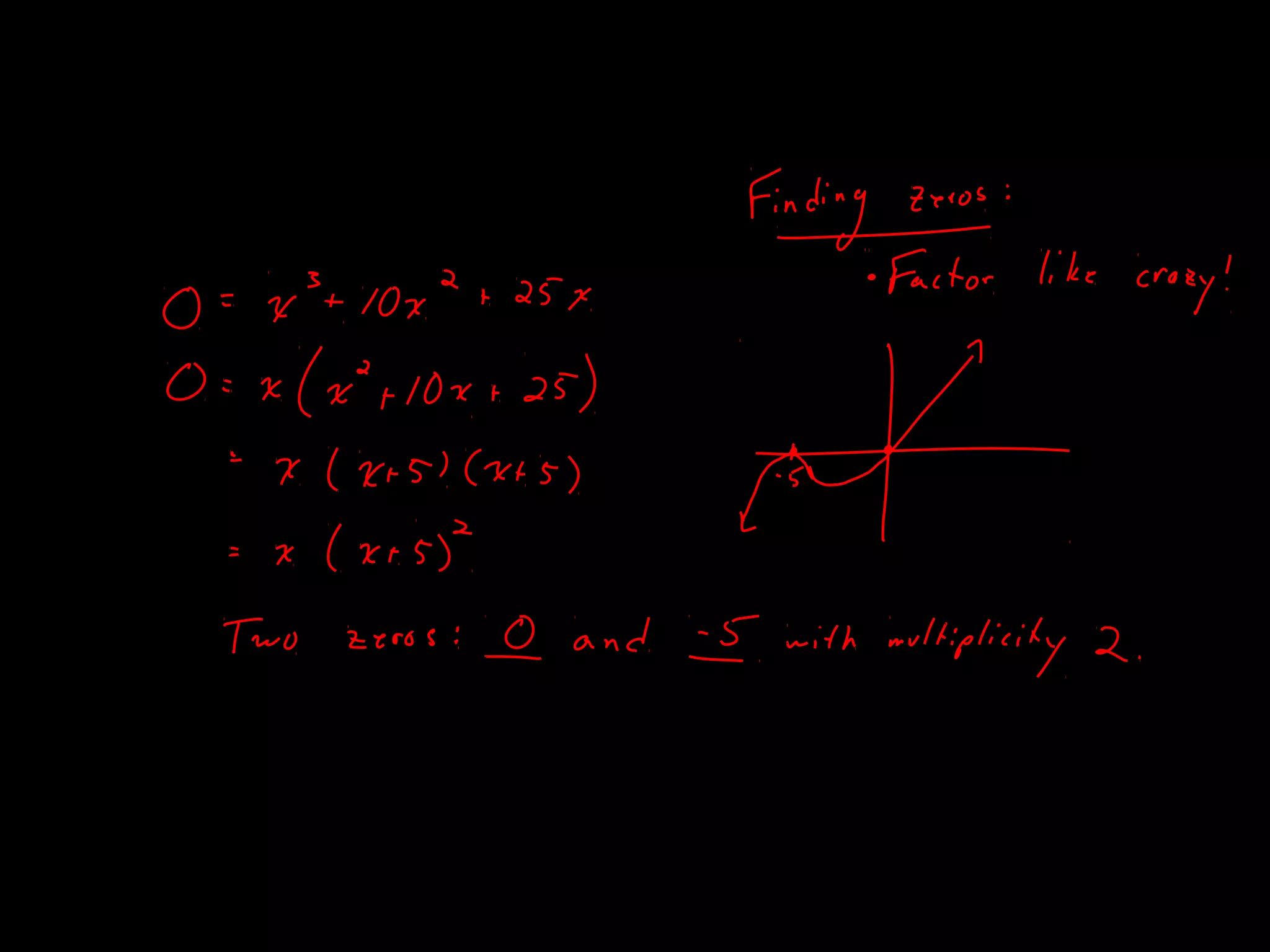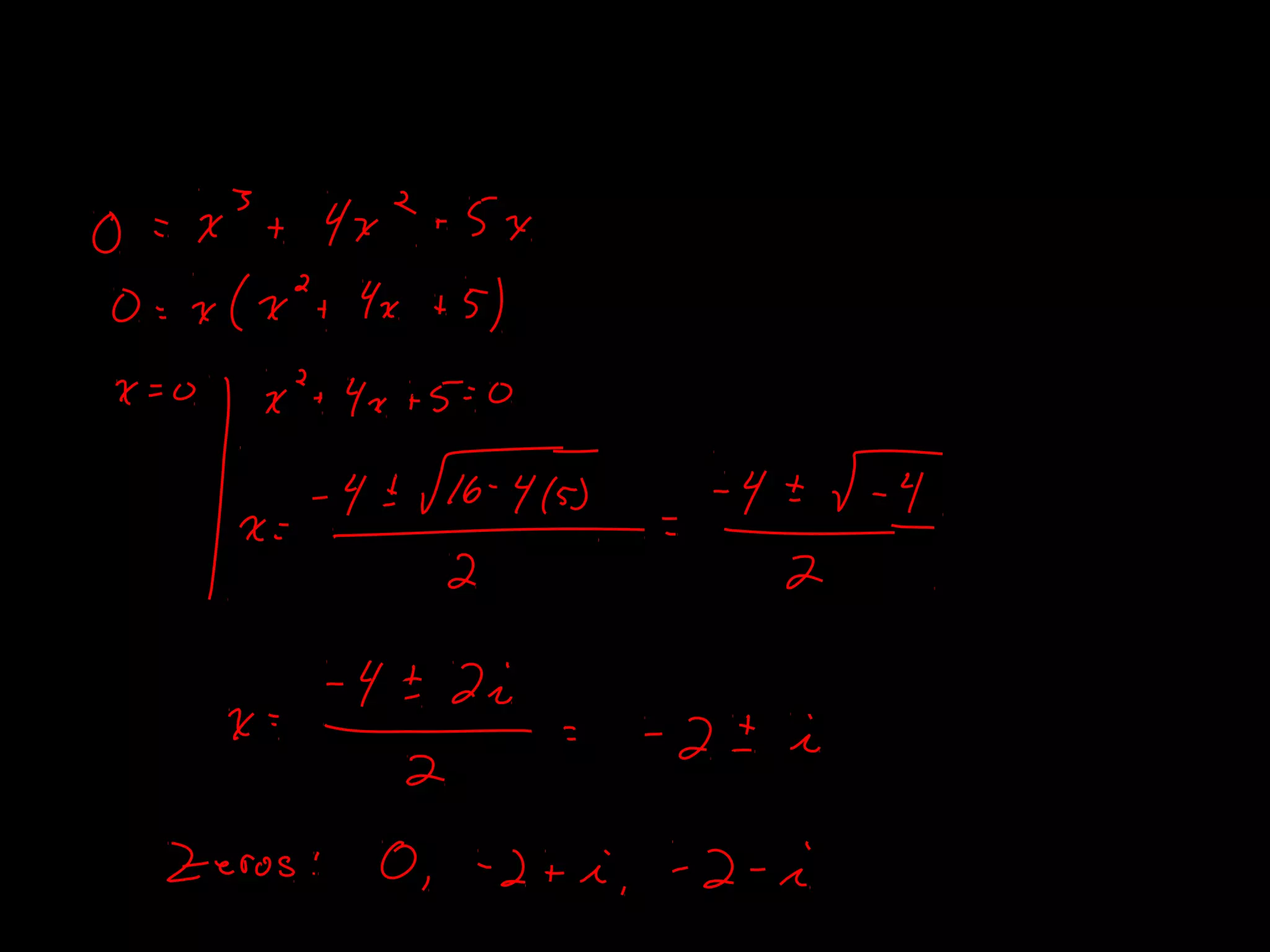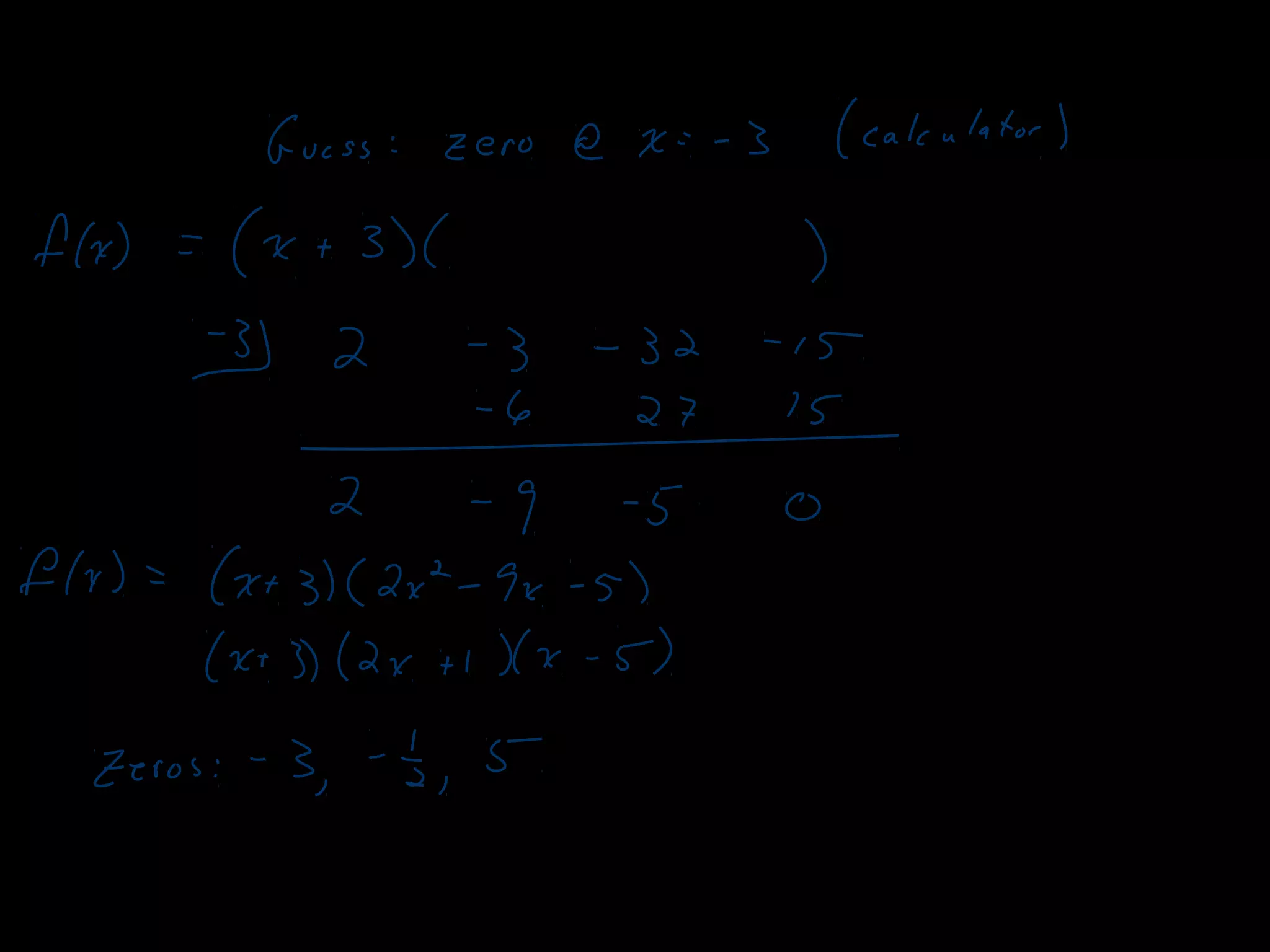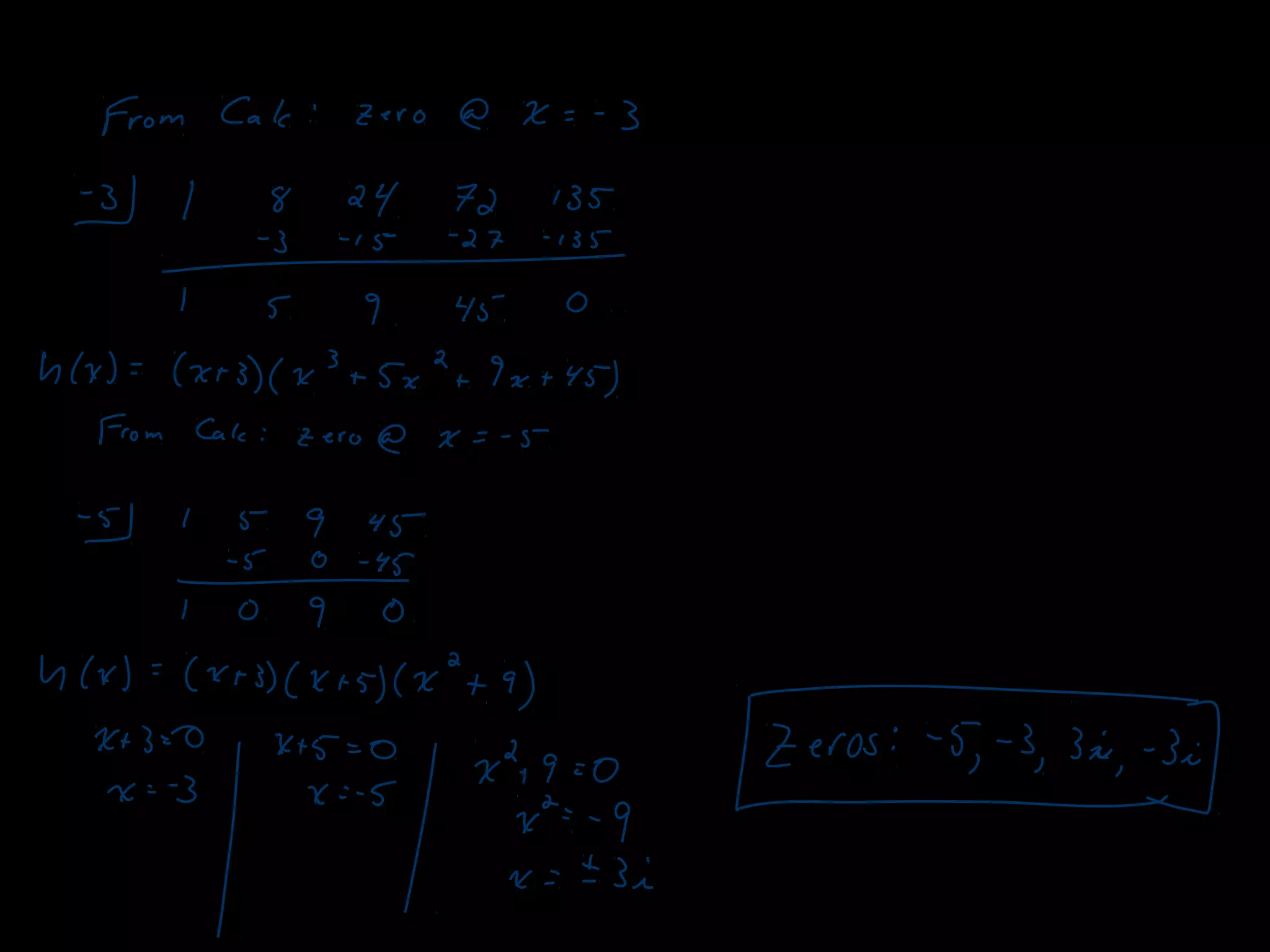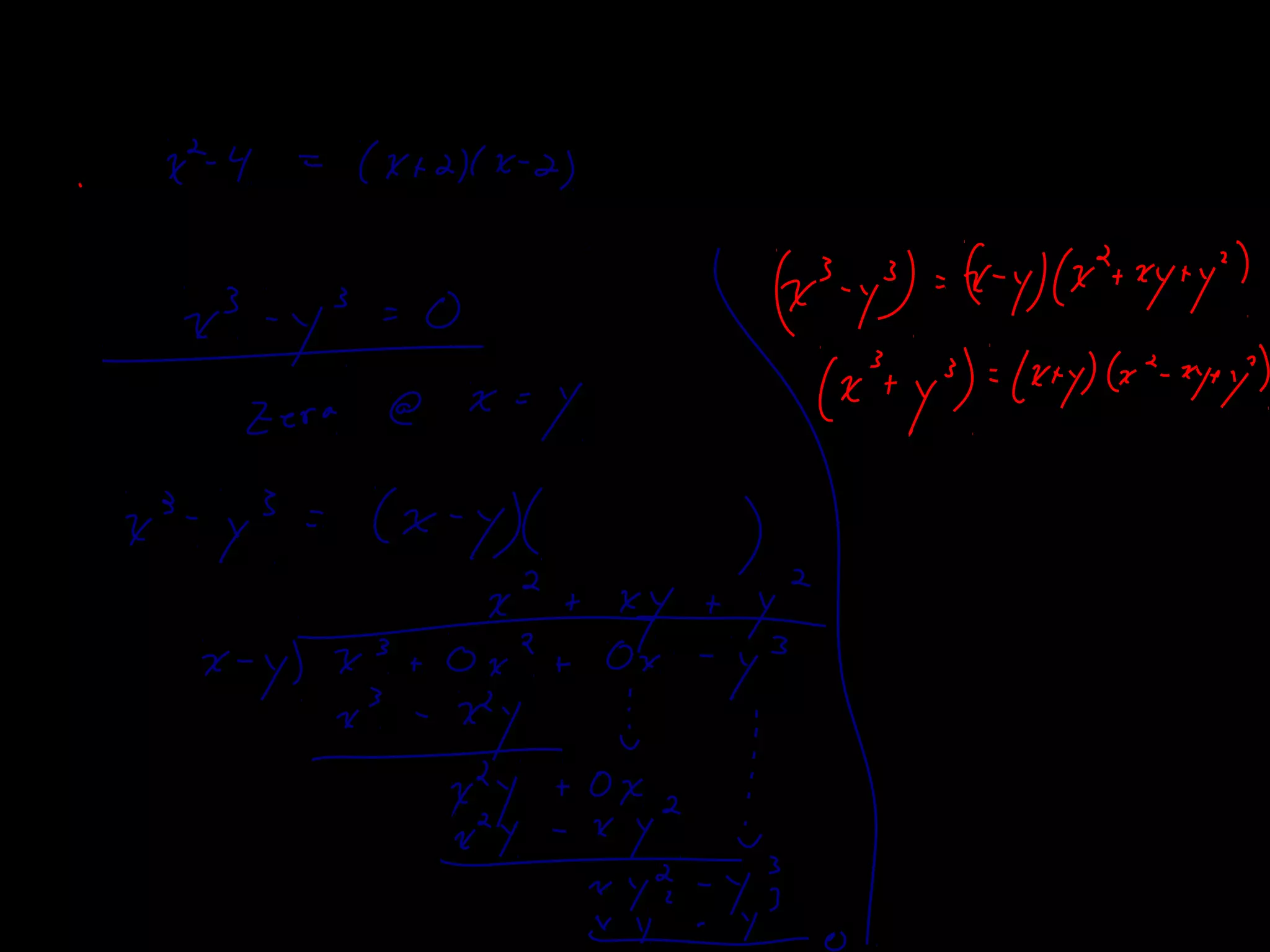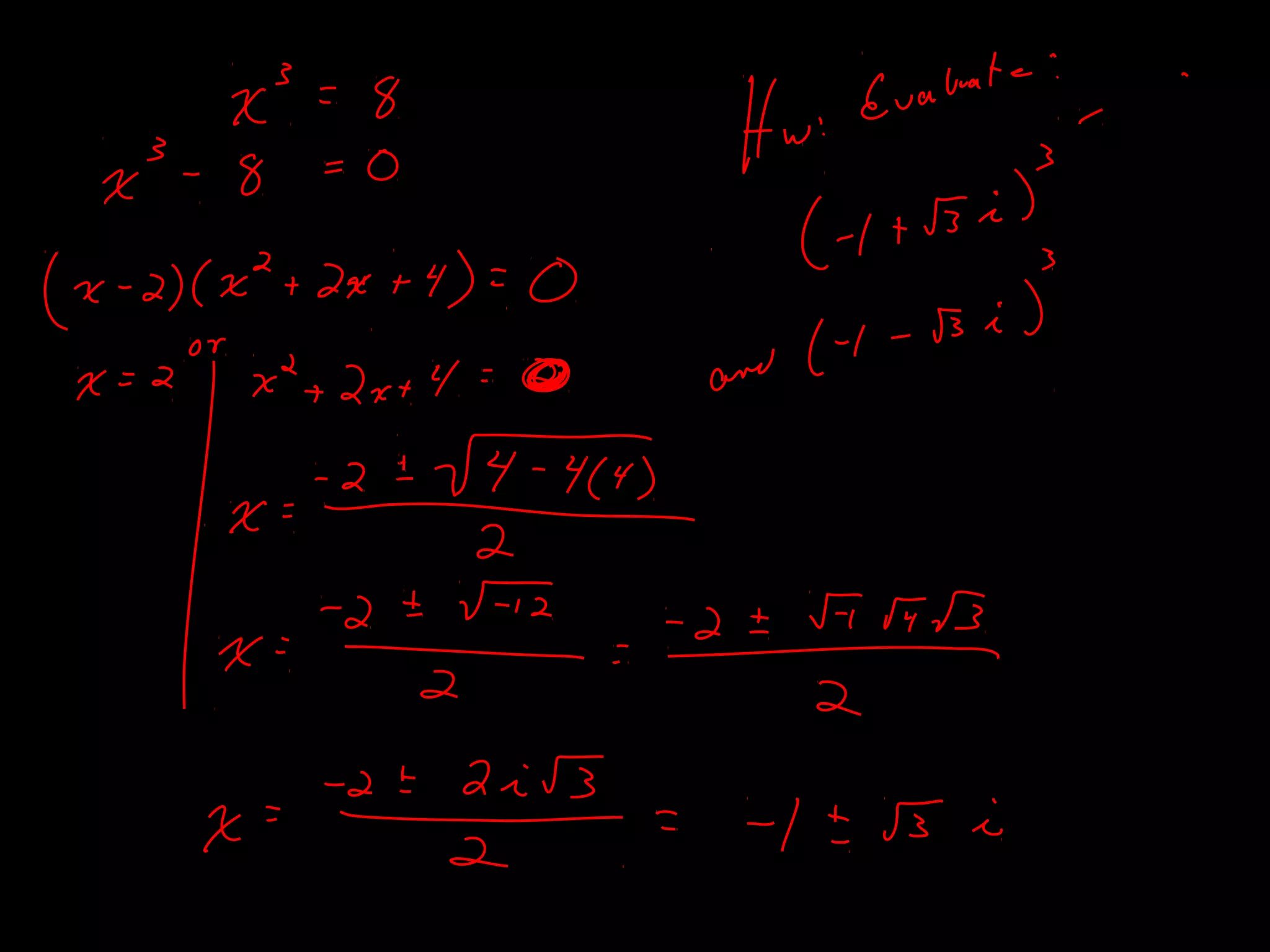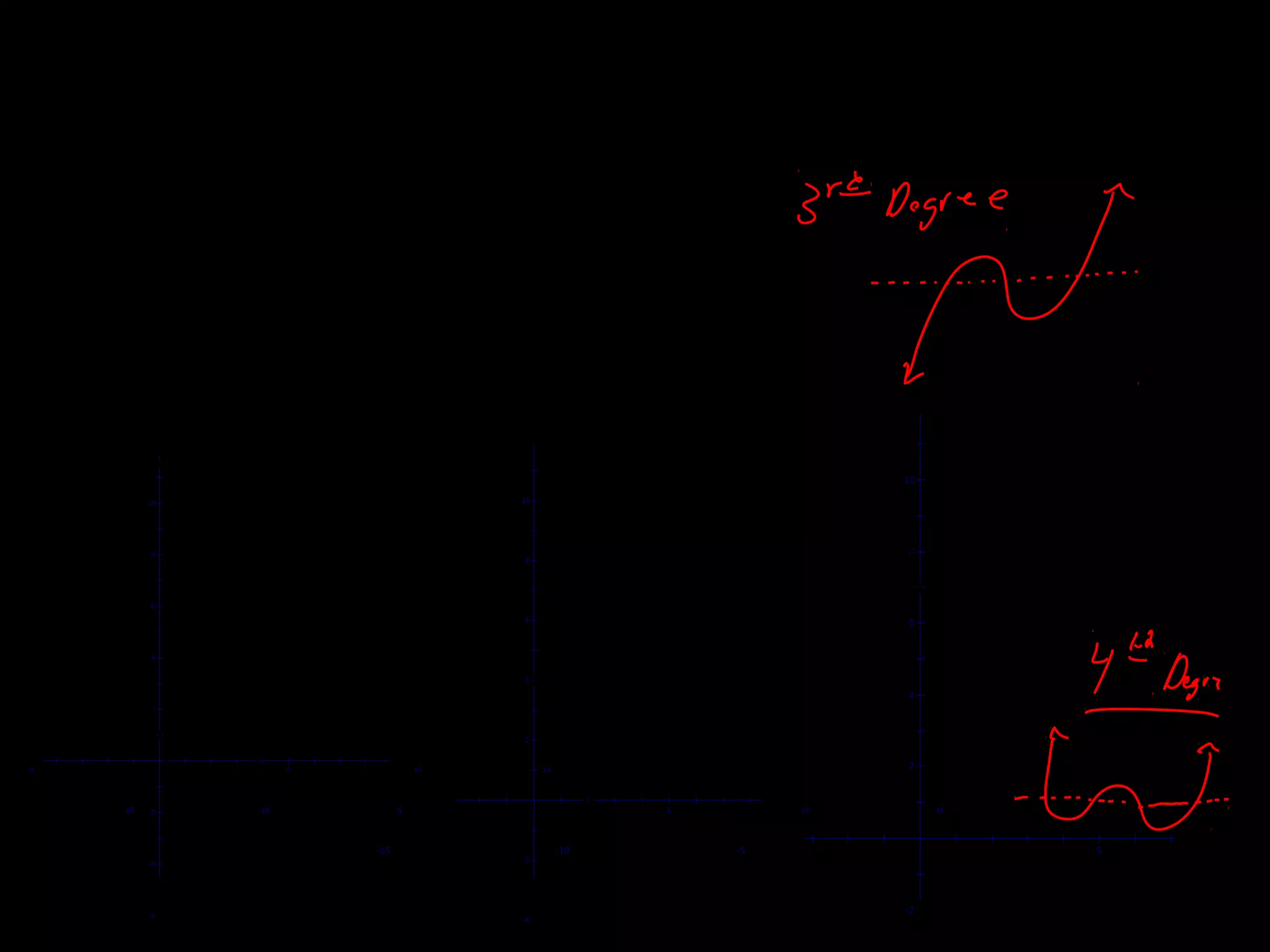
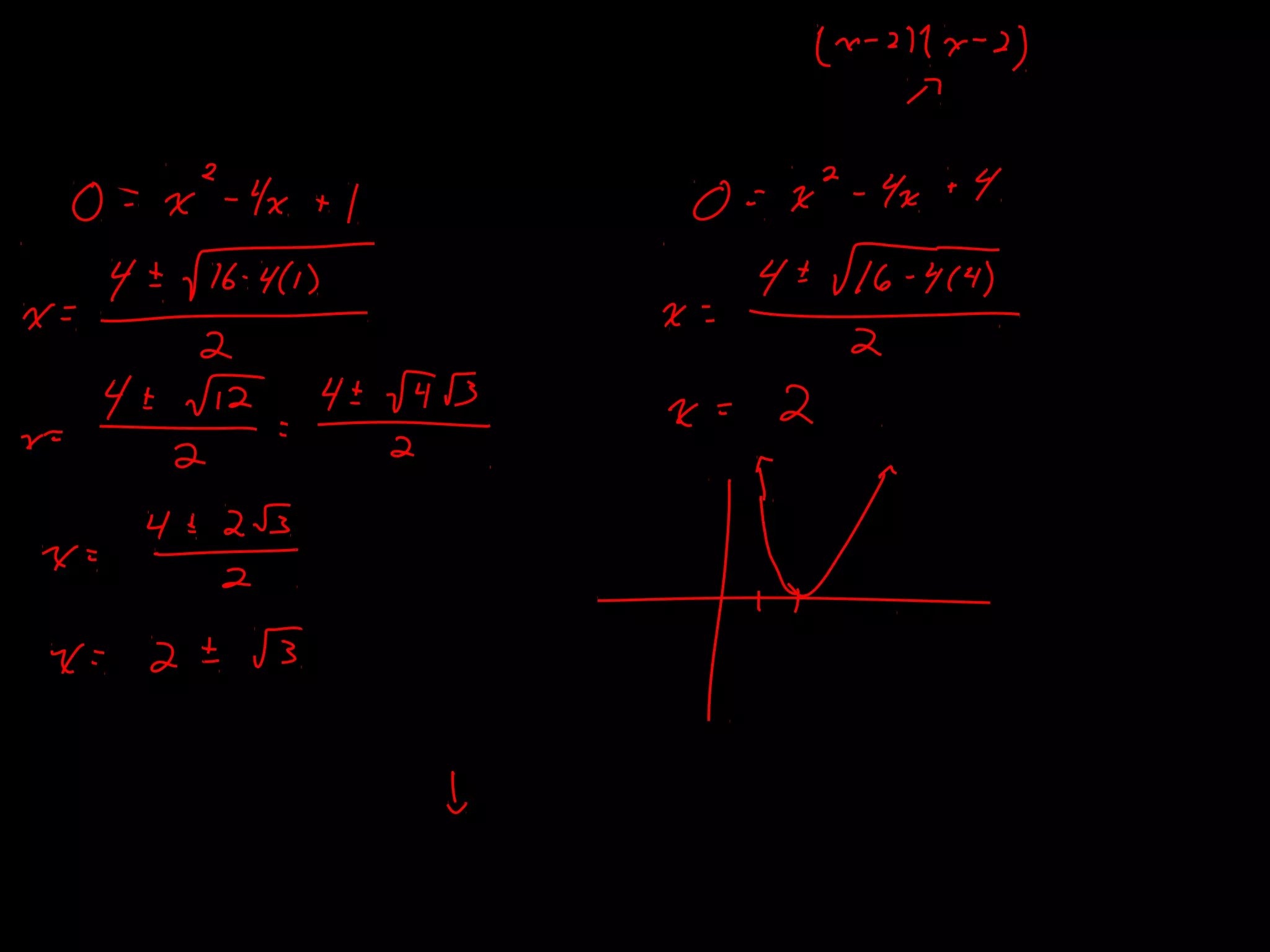
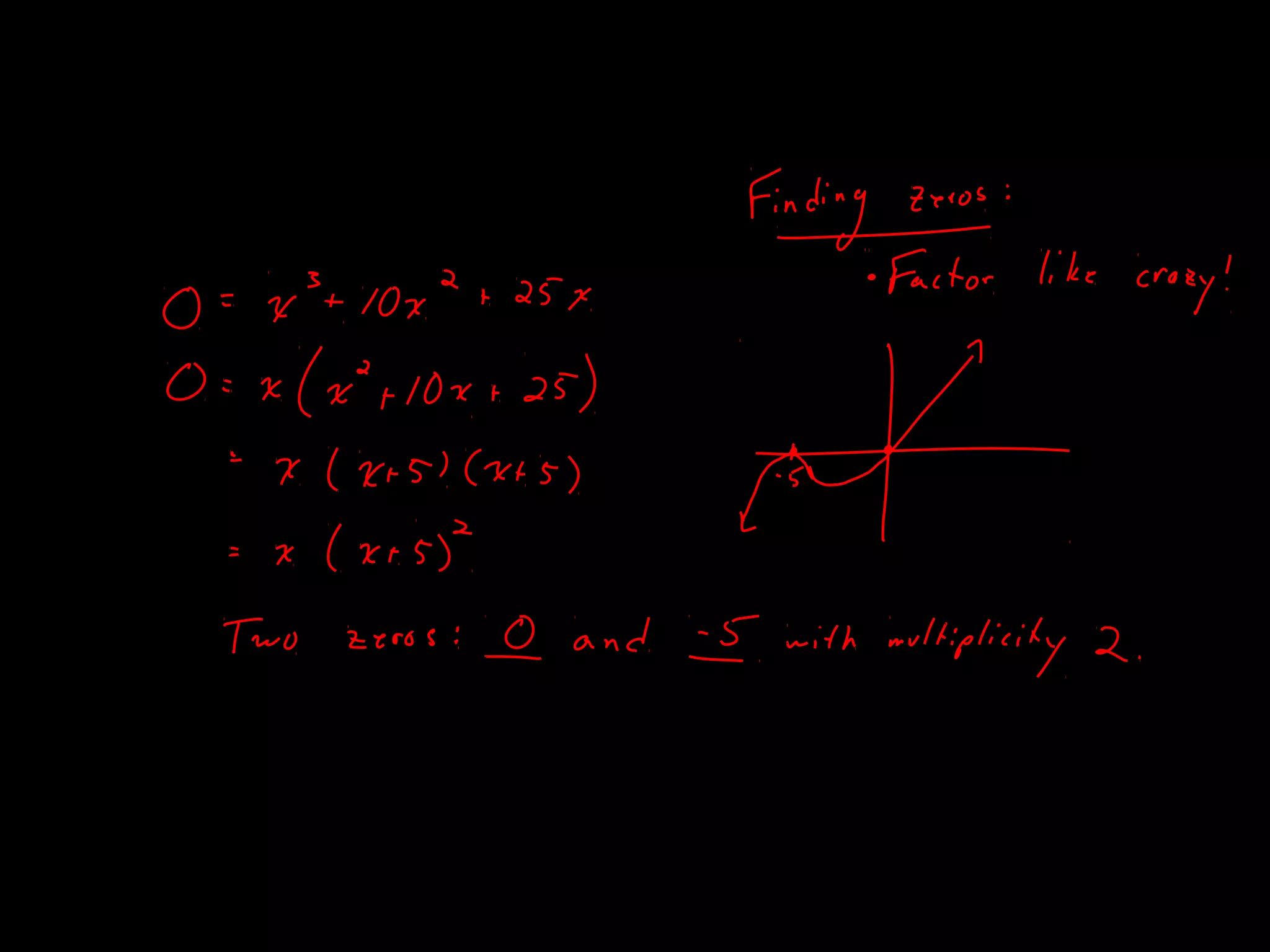
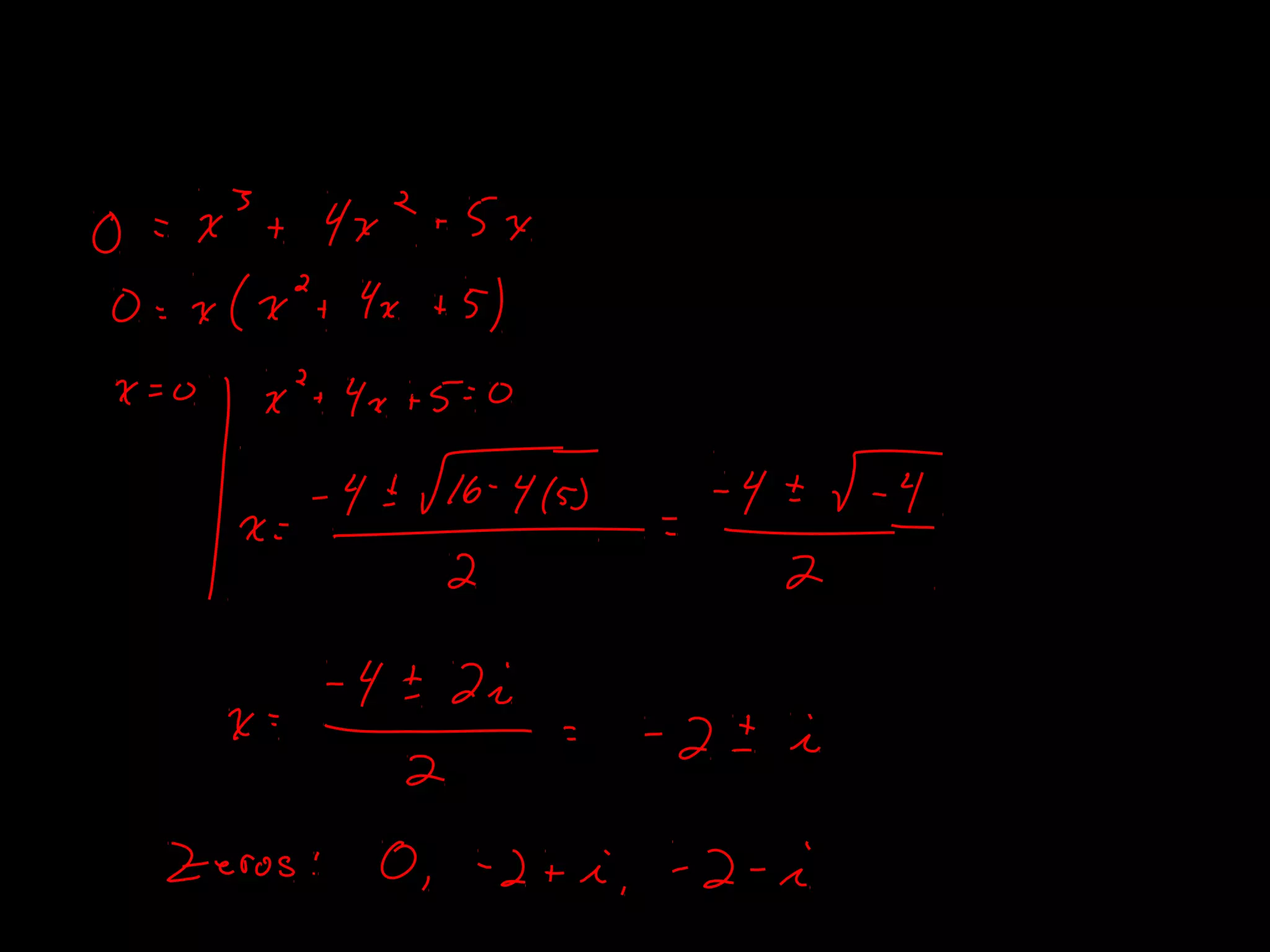
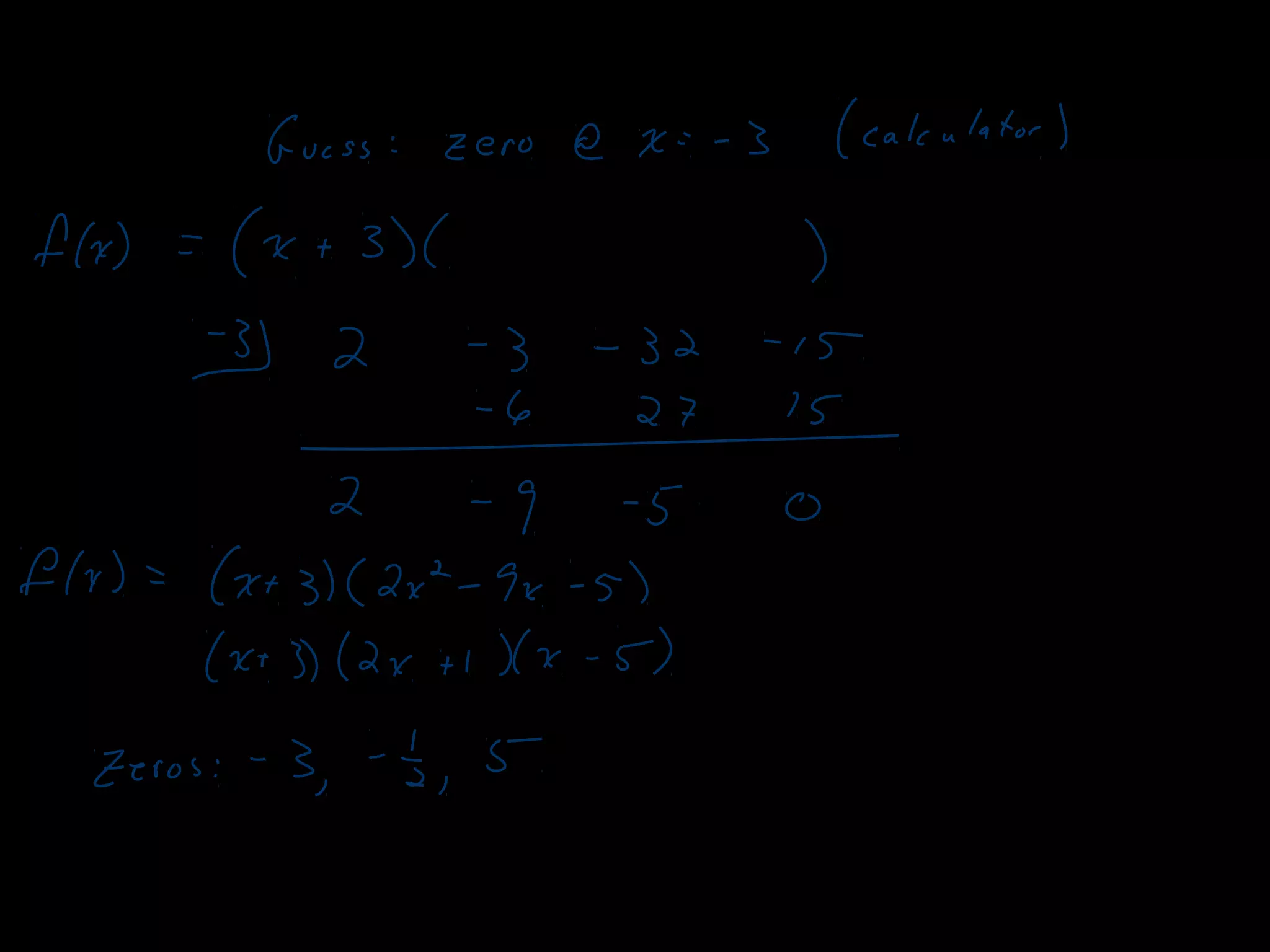
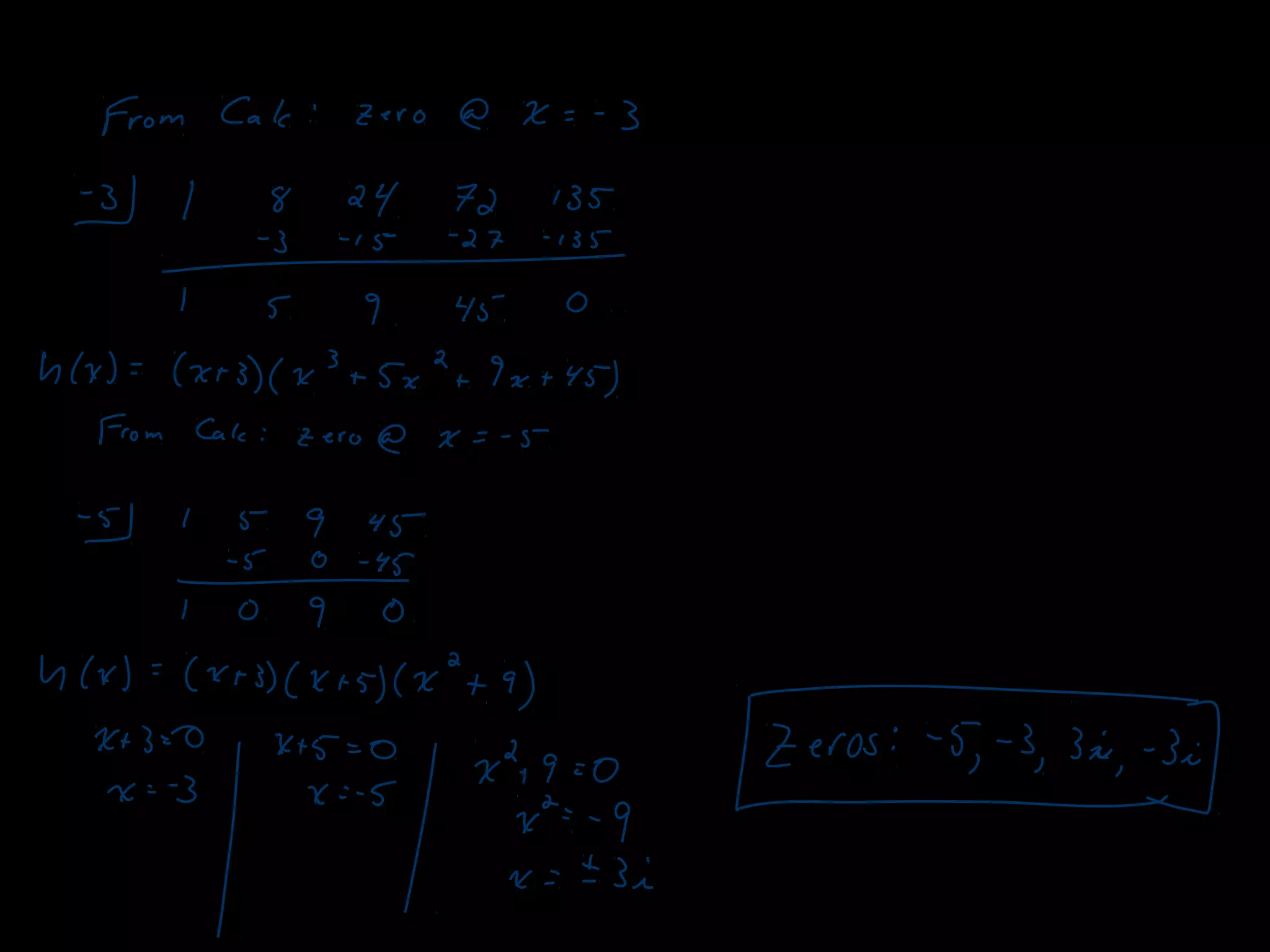
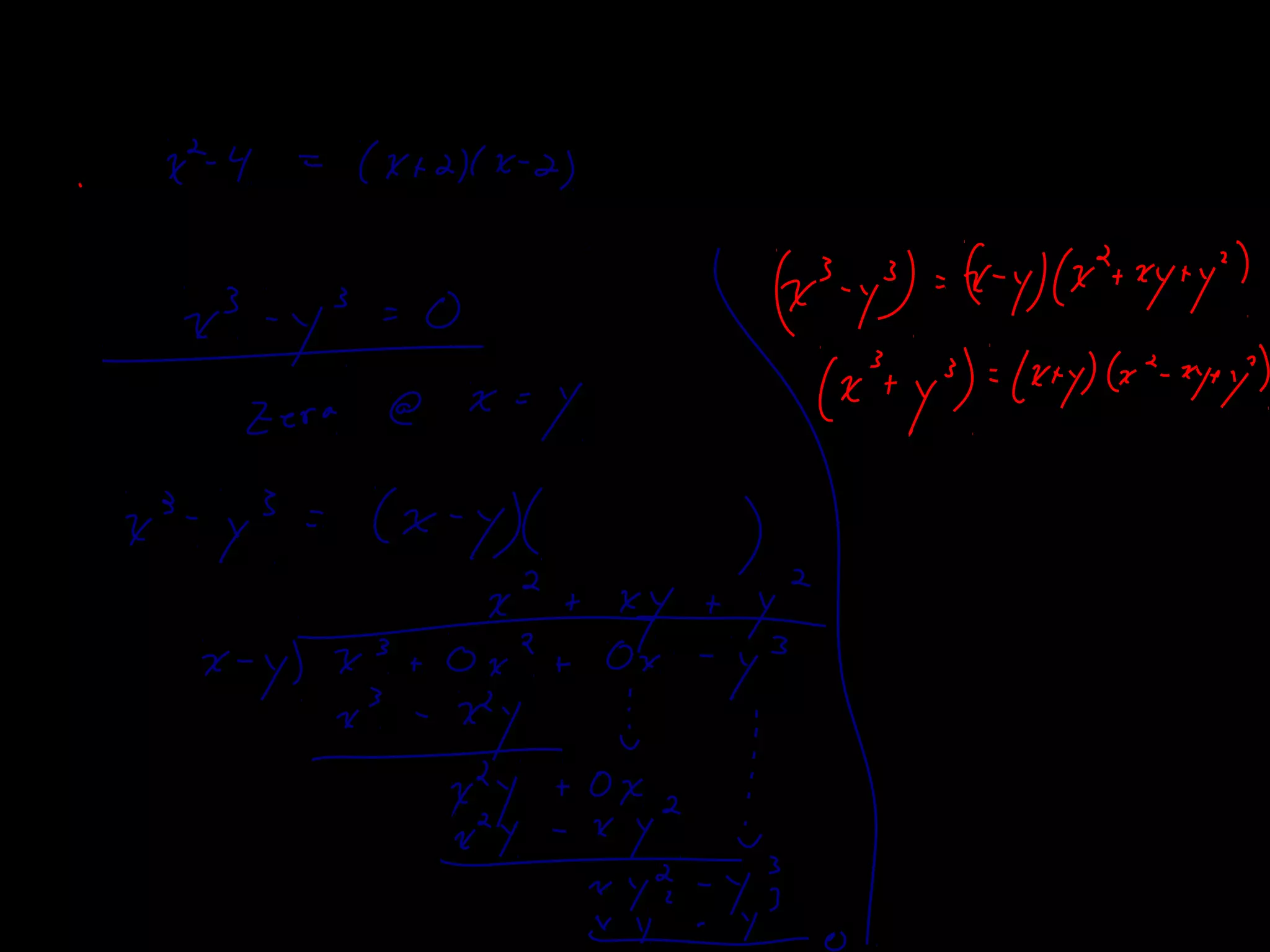
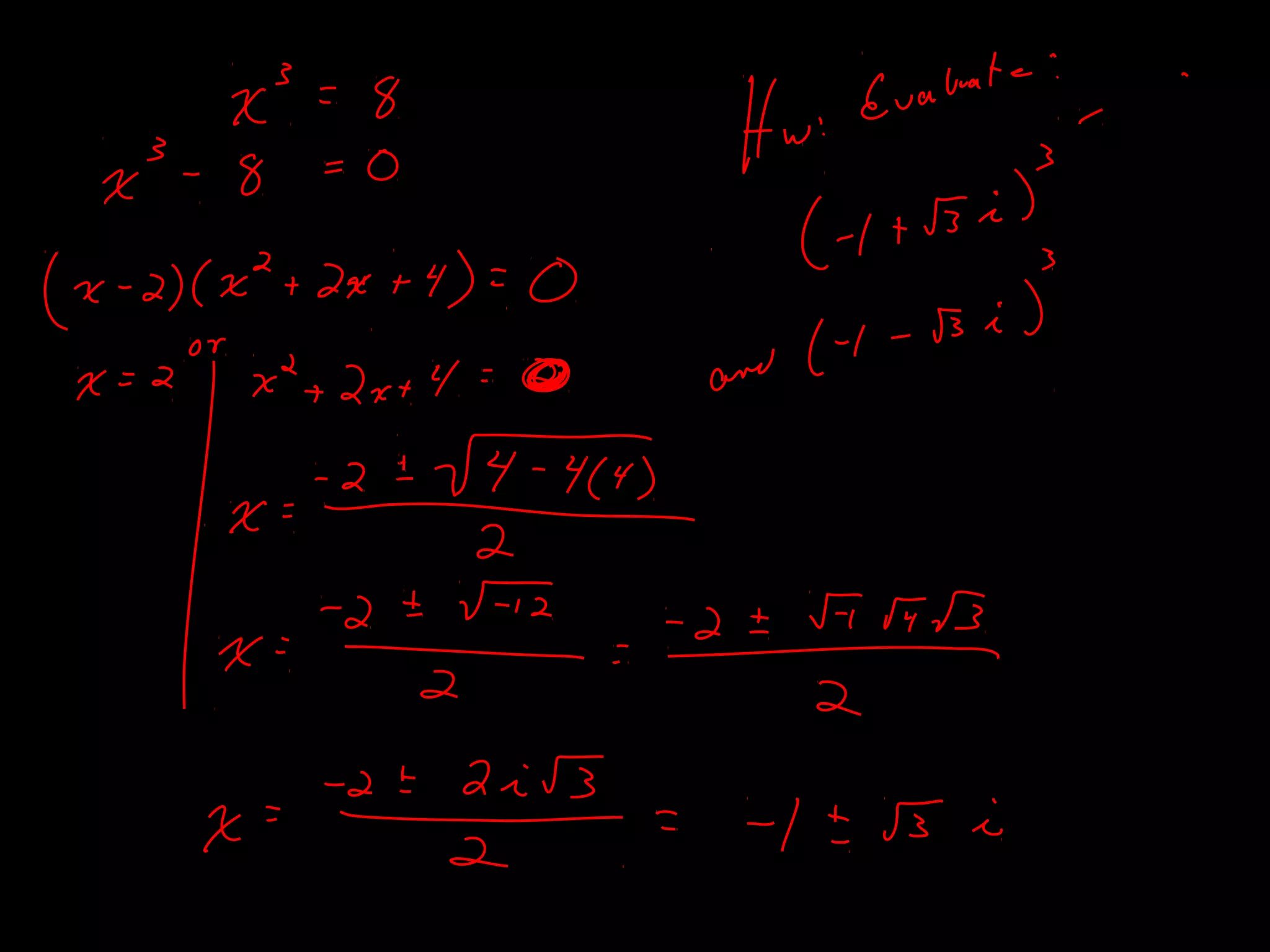
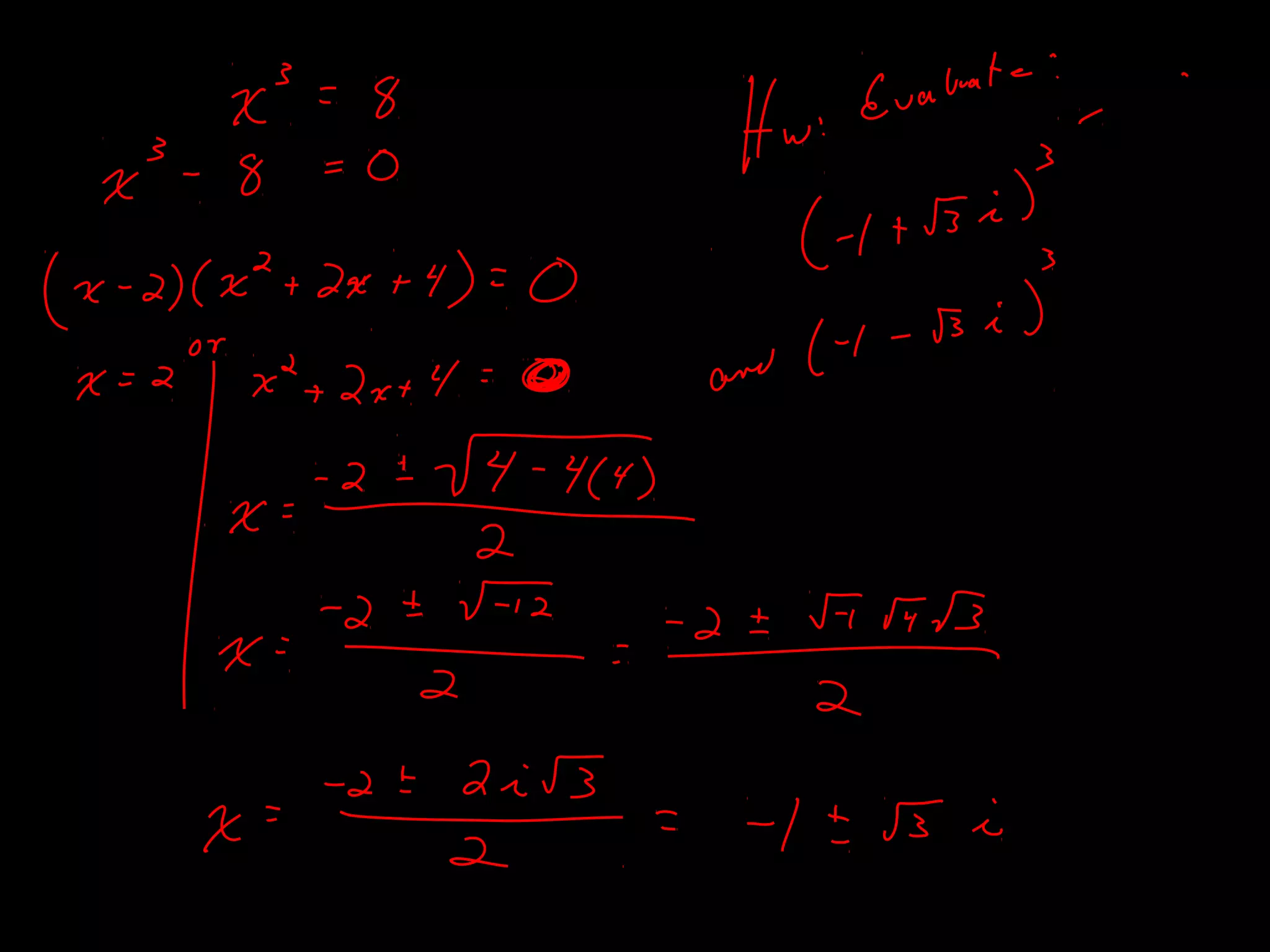
The document discusses several theorems related to polynomials: 1) The Fundamental Theorem of Algebra states that any polynomial of degree greater than 1 with complex coefficients has at least one complex zero. 2) A polynomial of degree n has at most n zeros. 3) A polynomial of degree n greater than 1 with complex coefficients has exactly n complex zeros, if multiplicities are counted.

1. The Fundamental Theorem of Algebra
If p(x) is any polynomial of degree n>1 with complex coefficients, then p(x)
has at least one complex zero.
A related theorem:
A polynomial of degree n has at most n zeros.
10
8
6
4
2
-2
-4
-6
-5 5 10 15
10
8
6
4
2
-2
-4
-15 -10 -5 5 10 15
f x( ) = x-2( )2
10
8
6
4
2
-2
-15 -10 -5 5
f x( ) = x-2( )2+3

2. Finding Zeros:
14)( 2
+−= xxxp 44)( 2
+−= xxxp
a
acbb
x
2
42
−±−
=

3. Multiplicity of Zeros:
If a polynomial has the same zero more than once, we describe that zero’s
multiplicity:
Ex:
Another theorem:
A polynomial of degree n>1 with complex coefficients has exactly n
complex zeros, if multiplicities are counted.
xxxxp 2510)( 23
++=

4. Complex Zeros
xxxxp 54)( 23
++=

5. 153232)( 23
−−−= xxxxf

6. 12112)( 23
−−−= xxxxg

7. 13572248)( 234
++++= xxxxxh

8. Factoring Sums and Differences of Powers
Recall that can be factored into .
What about ?
22
yx − ( )( )yxyx −+
33
yx −

9. Find the cube roots of 8.

10. Find the cube roots of 8.