Drift flux

Prof. G. Das
Department of Chemical Engineering
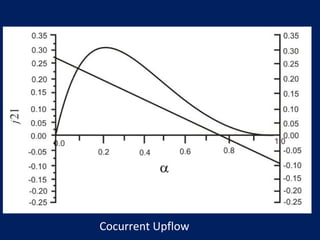
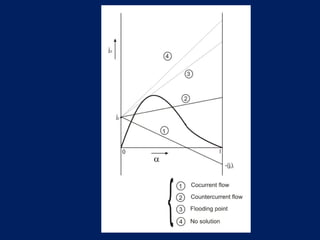
The Drift Flux Model
Lecture – 13
Indian Institute of Technology, Kharagpur

• Simplicity
• Applicable to a wide range of two phase flow problems of practical
interest
- bubbly, slug and drop regimes of gas-liquid flow
- fluidised bed of fluid particle system.
• Rapid solution of unsteady flow problems of sedimentation and
foam drainage
• Useful for the study of system dynamics and instabilities caused by
low velocity wave propagation namely void propagation.
Advantages

• A starting point for extension of theory to complicated problems of
fluid flow and heat transfer where two and three dimensional effects
such as density and velocity variations across a channel are
significant.
•Important for scaling of systems.
•Detailed analysis of the local behaviour of each phase can be carried
out more easily if the mixture responses are known

General Theory
08/14/16
Application- Bubbly
flow, slug flow, drop
regimes of gas-liquid
flow as well as to
fluidized bed
Volumetric Flux
Drift flux ( )21 2 TPj u jα= −
( ) ( )12 11 TPj u jα= − − ( )1 211 TPj j jα= − −
2 21TPj j jα= +
2 21
2
1
TP
j j
j j
α
 
= − ÷
 
( )1 1 2 2 21
2 1TP
TP TP
j j j
j j
ρ ρ
ρ ρ ρ
+
= + −
TP
Q
j
A
= 1 1(1 )j uα= − 2 2j uα=
21 2(1 )u j jα α α= − = −
Relative velocity between the phases taken care of by the
concept of drift flux

1
1 1 1 1 1u u b f p
t
ρ
∂ 
+ ∇ = + − ∇ ∂ 
u
2
2 2 2 2 2
u
u u b f p
t
ρ
∂ 
+ ∇ = + −∇ ∂ 
Kinematic Constitutive Relation
In two fluid model, the momentum balance equations for unit
volume of the individual phases in three dimensional vector form
is:

1 1
1 1 1 1
u u p
u b f
t z z
ρ
∂ ∂ ∂ 
+ = + − ∂ ∂ ∂ 
2 2
2 2 2 2
u u p
u b f
t z z
ρ
∂ ∂ ∂ 
+ = + − ∂ ∂ ∂ 
For one dimensional flow, eqns can be resolved in the direction of
motion to give:

1
10
1
Fdp
g
dz
ρ
α
= − − +
−
2
20
Fdp
g
dz
ρ
α
= − − +
( )1 1 12 11 wF f F Fα= − = −
Under steady state inertia dominant conditions the aforementioned
equations become:
Where F1
and F2
are the equivalent f’s per unit volume of the
whole flow field. Thus
( )2 2 2 12wF f F Fα= = − +

Since action and reaction are equal
F1 = F2= - F12
Therefore the equations become:
12
10
1
Fdp
g
dz
ρ
α
= − − +
−
12
20
Fdp
g
dz
ρ
α
= − − −

( ) 12 12
2 10
1
F F
gρ ρ
α α
= − + +
−
or
( ) ( )12 1 21F gα α ρ ρ= − −
On subtracting momentum eqn for phase 1 from that
of phase 2, we get

2 (1 )n
ju u α∞= −
This gives:
21 (1 )n
j u α α∞= −
F12=F12 (α, j21 )

The values of u2j
for a few representative cases are as follows:
For the viscous regime,
( ) ( ) { ( )}
( ){ }
4/3
* *1/3 1.5
2
2 6/72 * *
2
11 ( )
10.8
( )
d d
j
d d
r rfg
u
r r f
ψ ψα αµ ρ
ρ ψ α
+− ∆
≈  ÷
+ 
Where
( ) ( )
1/ 2 1
1
TP
f
µ
α α
µ
= −
( ) ( ){ }
3
4/7
0.75* *
0.55 1 0.08 1d dr rψ = + −

* 1
2
1
d d
g
r r
ρ ρ
µ
 ∆
=  ÷
 
Where rd
is the radius of the dispersed phase
For Newton’s regime ( 34.65)dr∗
≥
( )
( ) }{
1/ 2
1.5
2 6/7
1
18.67
2.43 1 ( )
1 17.67
d
j
r g
u f
f
ρ
α α
ρ α
 ∆
= − × ÷
+ 

For distorted fluid particle regime
where Nμ the viscosity number is given as:
( ) 8/3
0.11 1 /Nµ ψ ψ ≥ + 
1
1/ 2
1
N
g
µ
µ
σ
ρ σ
ρ
=
 
 ÷
∆ 

( )
( )
( )
1.75
1/ 4
2
2 1 22
1 2.25
2 1
1
2 1
1
j
g
u
α
σ ρ
α µ µ
ρ
α µ µ
 −
 ∆ 
≈ × − ≈ ÷
  
− >>
For churn turbulent flow regime
( )
1/ 4
1/41 2
2 2
1
2 1j
g
u
ρ ρσ ρ
α
ρ ρ
  −∆
= − ÷
∆ 

1/ 4
1 2
2
2
g ρ ρσ ρ
ρ ρ
  −∆
≈  ÷
∆ 
It may be noted that in the aforementioned expression for u2j
, the
proportionality constant is applicable for bubbly flows and
1.57 for droplet flows.
2
2
1
0.35j
g D
u
ρ
ρ
 ∆
=  ÷
 

In the absence of infinite relative velocity,
21
21
0 0
0 1
j at
j at
α
α
= =
= =

Graphical Technique for solution of Drift Flux Mod

Countercurrent flow with Gas Flowing up and Liquid flowing down
for a constant gas and different liquid velocities

Countercurrent flow with Gas Flowing down and Liquid flowing up

Drift Flux Model for Solid as the dispersed phase

Corrections to the one dimensional model:
2 21j j jα= +
( )j dA
j
dA
α
α =
∫
∫

It may be noted that
j jα α≠
Since
dA jdA
j
dA dA
α
α
   
   =
   
   
∫ ∫
∫ ∫

0
j
C
j
α
α
=
0CWhere is the ratio of averae of product of flux and
concentration to product of averages or
( )
0
1
1 1
j dA
AC
dA jdA
A A
α
α
=
   
      
∫
∫ ∫

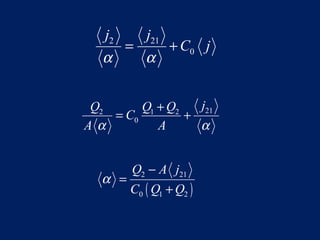
2 21
0
j j
C j
α α
= +
212 1 2
0
jQ Q Q
C
A Aα α
+
= +
( )
2 21
0 1 2
Q A j
C Q Q
α
−
=
+

0
2
1
2
C
m n
= +
+ +
[1 ]wα
α
−
< >
0CEstimation of
For fully developed bubbly flow (Ishii)
0 0 ,
g
l l
GD
C C
ρ
ρ µ
 
=  ÷
 
Assuming power law profiles for α and j

For flow in a round tube
Co= 1.2 – 0.2 /g lρ ρ
For flow in a rectangular channel
Co = 1.35 – 0.35 /g lρ ρ
For developing void profile (0< α<0.25)
-18
0 gC = ( 1.2 - 0.2 ) ( 1- e ) round tubel
α
ρ ρ−
-18
0 gC = ( 1.35 - 0.35 ) ( 1- e ) rectangular channel.l
α
ρ ρ−

For boiling bubbly flow in an internally heated annulus
3.12< >0.212
Co= 1.2 - 0.2 [1 - e ]
g
l
α
ρ
ρ
 
 
  
In downward two-phase flow for all flow regimes
0C =(- 0.0214<j*> + 0.772) + (0.0214<j*> + 0.228) for (-20) <j*> < 0
g
l
ρ
ρ
≤
0.00848[<j*>+20] 0.00848[<j*>+20]
oC =(0.2e +1) - 02e for < j*> < (-20)
g
l
ρ
ρ
 
 ÷
 ÷
 
Where <j*
> =
2 j
j
u

Void profile changes from concave
to convex due to
• Wall nucleation and delayed transverse
migration of bubbles towards centre
• Subcooled boiling regime
• Injecting gas into flowing liquid through
porous tube wall
• Adiabatic flow at low void fraction when small
bubbles tend to accumulate near the walls
• Droplet or particulate flow in turbulent regime

08/14/16
Evaluation of terminal velocity
Bubbly flow

08/14/16
Bubble formation at Orifice
• Spherical bubble of radius Rb attached to orifice of radius Ro
• Largest bubble at static equilibrium
• Radius of bubble-blowing through-small orifice at low rates
• More accurate
34
( ) 2
3
b f g oR g Rπ ρ ρ π σ− =
1
3
3
2 ( )
o
b
f g
R
R
g
σ
ρ ρ
 
≈ 
−  
1
3
1.0
( )
o
b
f g
R
R
g
σ
ρ ρ
 
≈  
−   1
2
0.5
( )
o
f g
R
g
σ
ρ ρ
 
>  
−  

08/14/16
Influence of shear stress
• Shear stress determine bubble size in
forced convection /mechanically agitated system
• Shear stress influence –
• Size of bubbles form away from point of formation
 Max bubble size which is stable in flow
• Mechanical power dissipated/unit mass
3 2
5 5
0.725( ) ( )
f
p
d
M
σ
ρ
−
=
p
m

08/14/16
Formation of bubble by
Taylor instability
• Formed by detachment from blanket of gas or vapor
over a porous or heated surface
• Formation not identical with “Taylor instability” of a
fluid below a denser fluid but physics similar
1
2
( )
b
f g
R
g
σ
ρ ρ
 
≈ 
−  

08/14/16
Formation by evaporation or mass transfer
• By evaporation of surrounding liquid/ release of gases
dissolved in liquid
• Bubble form-nucleation centre-impurities in fluids/pits,
scratches, cavities on wall
• contact angle in degrees
• Valid for quasi-static case-not for bubbles formed during
boiling
1
2
0.0208
( )
o
b
f g
R
D
g
σ
β
ρ ρ
 
≈  
−  
β

08/14/16
INFLUENCE OF CONTAINING
WALLS
In finite vessel: ub
<u∞
ub
/u∞
=fn(d/D), D=Tube diameter
In region 5 for large inviscid bubbles
 d/D < 0.125 , ub
/u∞
=1
 0.125 < d/D < 0.6 , ub
/u∞
=1.13 e-d/D
 0.6 < d/D , ub
/u∞
=0.496 (d/D)-1/2
[Bubbles behaves like slug flow bubbles in an inviscid fluid]

08/14/16
INFLUENCE OF CONTAINING WALLS
CONTINUED
• In viscous fluids:
ub
/u∞
=[1+2.4(d/D)]-1
For bubbles behaving as solid spheres
ub
/u∞
=[1+1.6(d/D)]-1
For fluid spheres & µg
<< µf
If d/D > 0.6 ,ub
/u∞
=0.12 (d/D)-2
At d/D = 0.6 , ub
/u∞
= 1-(d/D)/0.9 ( used to estimate ub
for d/D <
0.6)

Drift flux

More Related Content

Similar to Drift flux

Recently uploaded

Drift flux