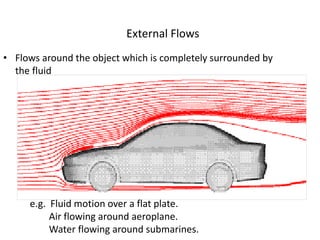
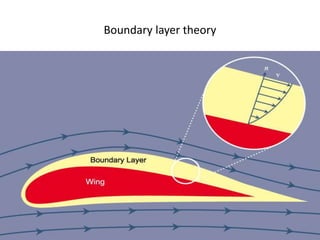
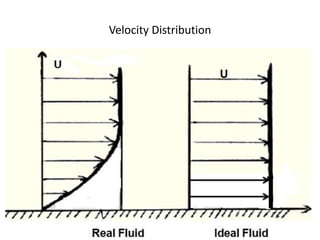
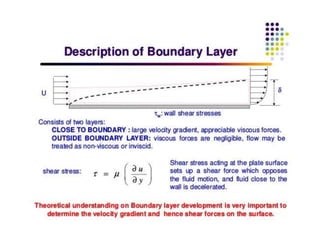
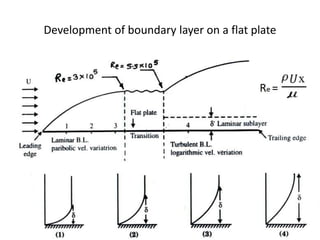
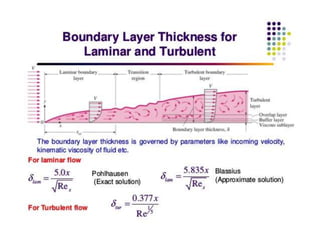
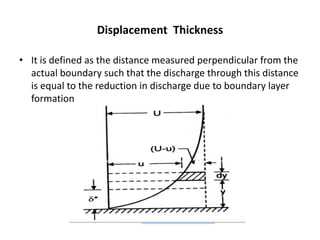
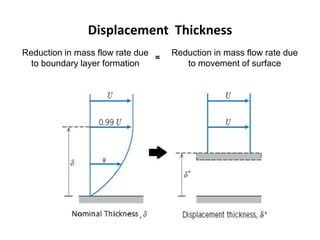
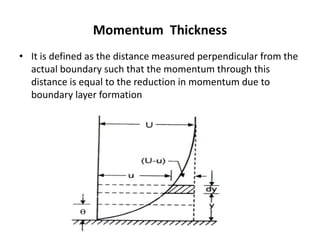
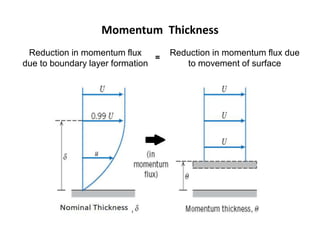
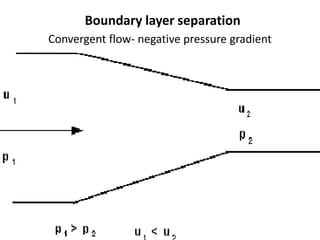
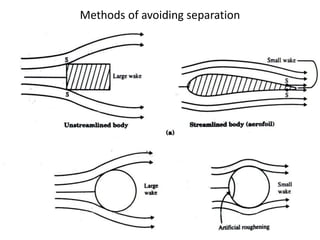
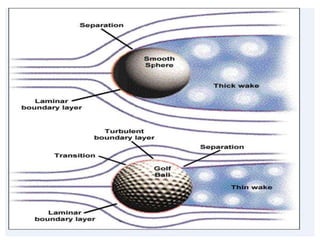
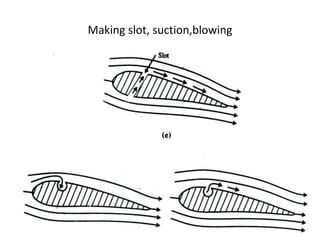
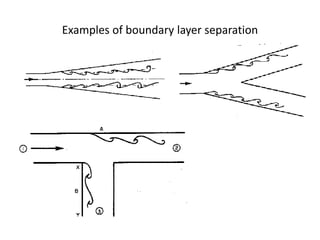
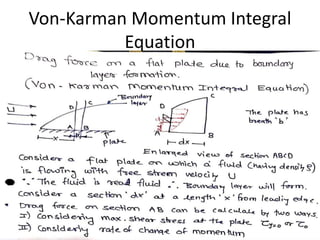
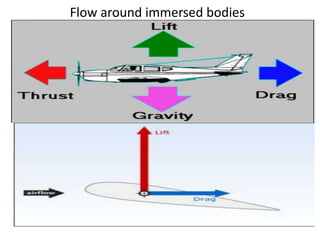
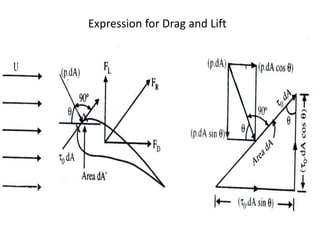
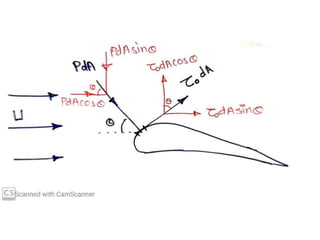
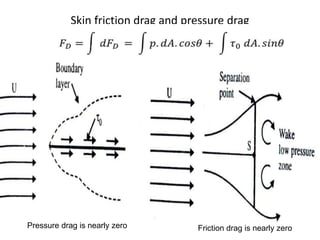
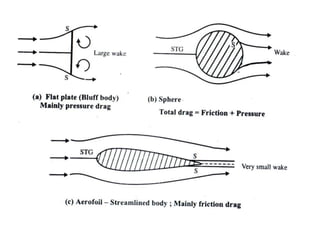
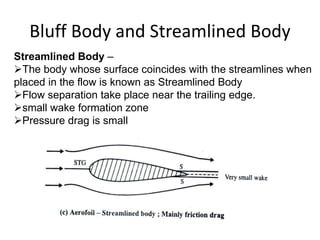
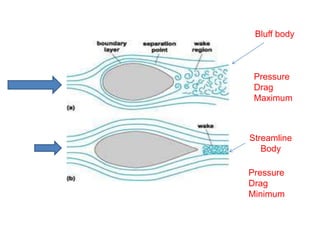
The document discusses the concept of external flows in fluid mechanics, focusing on boundary layer formation over flat plates and the factors affecting its thickness. It elaborates on various types of drag forces, including lift and drag on different body shapes, and explains the implications of boundary layer behavior on fluid motion. Additionally, it covers separation effects and methods to control them, along with a practical example to calculate terminal velocity.

1. External Flows (Unit- V)
• Fluid mechanics
• Prof. S. B. Powar
• Mechanical Engineering Department

2. • Boundary layer formation for flow over Flat plate, boundary
layer thickness:-displacement, momentum and energy.
• Separation of Boundary Layer and Methods of Controlling.
• Drag force on flat plate due to boundary layer formation
(Von-Karman momentum integral equation)
• Forces on immersed bodies: -Lift and Drag, types of bodies-
Bluff, streamline. Terminal velocity, drag and lift on stationary
and rotating cylinder. Drag on sphere.
Content

3. External Flows
• Flows around the object which is completely surrounded by
the fluid
e.g. Fluid motion over a flat plate.
Air flowing around aeroplane.
Water flowing around submarines.

4. Boundary layer theory

5. Boundary Layer
• A thin layer of fluid in the vicinity of boundary whose velocity
is affected due to viscous shear is called as Boundary Layer
• The region normal to the surface, in which velocity gradient
exists is known as Boundary Layer.

6. Velocity Distribution

8. Development of boundary layer on a flat plate

10. Factors affecting the growth of boundary layer
• The distance from the leading edge
• Viscosity of fluid
• The free stream velocity
• Density of fluid

11. Importance of boundary layer theory
• Calculation of friction drag of bodies in a flow.
• Calculation of pressure drag formed because of boundary
layer separation.
• Answers the important question of what shape a body
must have in order to avoid separation.

12. Nominal thickness
• It is defined as that distance from the boundary in which the
velocity reaches 99% of the main stream velocity

14. • Nominal thickness gives an approximate value of the boundary
layer thickness.
• For greater accuracy the boundary layer thickness is defined in
terms of certain mathematical expressions which are the
measures of the effect of boundary layer on the flow.

15. Displacement Thickness
• It is defined as the distance measured perpendicular from the
actual boundary such that the discharge through this distance
is equal to the reduction in discharge due to boundary layer
formation

16. Displacement Thickness
Reduction in mass flow rate due
to boundary layer formation
=
Reduction in mass flow rate due
to movement of surface

17. Consider a strip of height ‘dy’ and width ‘b’
Mass flow rate through the strip =
If there is no surface then Mass
flow rate through the strip =
Reduction in Mass flow rate
through the strip =

19. Displacement Thickness

20. Momentum Thickness
• It is defined as the distance measured perpendicular from the
actual boundary such that the momentum through this
distance is equal to the reduction in momentum due to
boundary layer formation

21. Momentum Thickness
Reduction in momentum flux
due to boundary layer formation
=
Reduction in momentum flux due
to movement of surface

22. MOMENTUM THICKNESS

23. Momentum Thickness

24. Energy Thickness
• It is defined as the distance measured perpendicular from the
actual boundary such that the kinetic energy through this
distance is equal to the reduction in kinetic energy due to
boundary layer formation

28. Convergent flow- negative pressure gradient
Boundary layer separation

29. Divergent flow-positive pressure gradient

30. • Convergent flow-negative
pressure gradient
• Favourable pressure
gradient
• Pressure decreases and
velocity increases
• Fluid particles are
accelerated
• Boundary layer is held in
place
• Divergent flow-positive
pressure gradient
• Adverse pressure gradient
• Pressure increases and
velocity decreases
• Fluid particles are
deaccelerated
• Adverse pressure gradient
may lead to negative
velocity or flow reversal
gradientpressure
favorable,0


x
P
0, adverse
pressure gradient
P
x




31. Boundary layer separation

33. Boundary Layer and separation
gradientpressure
favorable,0


x
P
gradientno,0


x
P
0, adverse
pressure gradient
P
x



Flow accelerates Flow decelerates
Constant flow
Flow reversal
free shear layer
highly unstable
Separation point

34. Effects of separation
• Large amount of energy is lost
• Pressure drag is increased and hence additional resistance to
movement of the body is developed
• Bodies are subjected to lateral vibrations

35. Methods of avoiding separation

37. Making slot, suction,blowing

38. Examples of boundary layer separation

39. Numerical on Boundary layer
separation

41. Von-Karman Momentum Integral
Equation

47. Flow around immersed bodies

48. Expression for Drag and Lift

51. Pressure Drag
(or)
Form Drag
Friction Drag
(or)
Skin Drag
(or)
Shear Drag

54. Skin friction drag and pressure drag
Pressure drag is nearly zero Friction drag is nearly zero

56. Bluff Body and Streamlined Body
Bluff Body –
The body whose surface does not coincide with the
streamlines when placed in the flow is known as Bluff Body
Flow separation take place much ahead of trailing edge.
Large wake formation zone

57. Bluff Body and Streamlined Body
Streamlined Body –
The body whose surface coincides with the streamlines when
placed in the flow is known as Streamlined Body
Flow separation take place near the trailing edge.
small wake formation zone
Pressure drag is small

58. Bluff body
Pressure
Drag
Maximum
Streamline
Body
Pressure
Drag
Minimum

59. • Drag Coeff For Different Body
Shapes

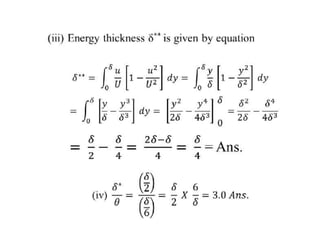
60. Terminal Velocity
The maximum constant velocity of a falling body with which
body is travelling is known as terminal velocity
Example- Sphere falling from sufficient height, Parachute with
man
At Terminal velocity
Weight of Body = Drag Force + Buoyant Force
W = FD + FB
A parachutist has a mass of 90 kg and a projected frontal area of 0.30
m2 in free fall. The drag coefficient based on frontal area is found to be
0.75. If the air density is 1.28 kg/m3, the terminal velocity of the
parachutist will be: [IES-1999]
(a) 104.4 m/s (b) 78.3 m/s
(b) (c) 25 m/s (d) 18.5 m/s

61. Thank You
Questions?