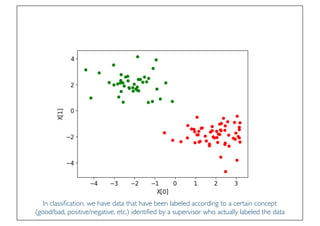
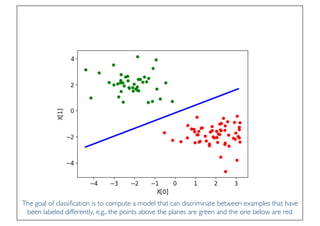
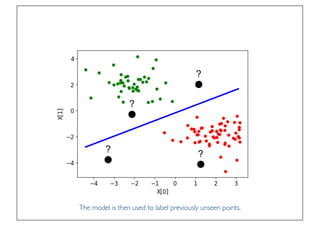
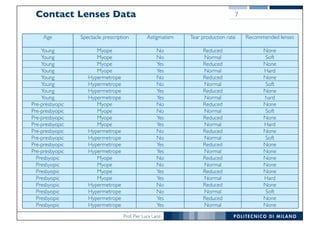
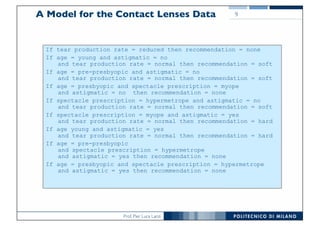
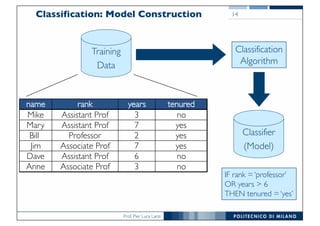
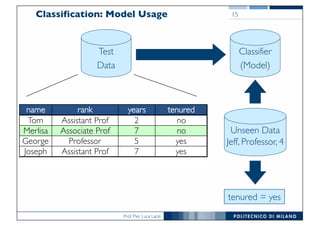
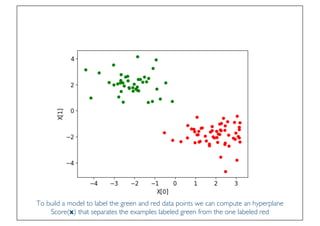
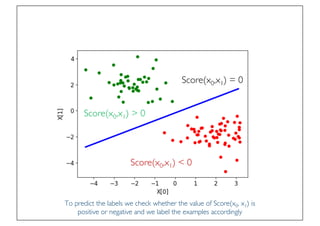
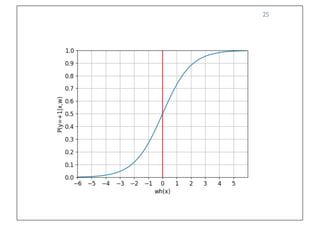
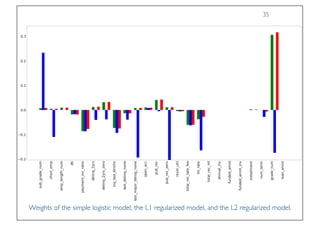
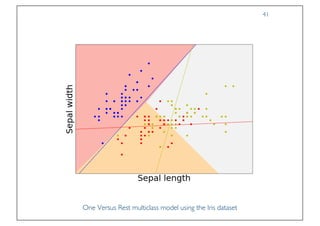
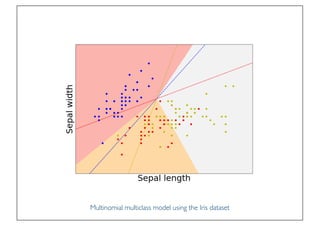
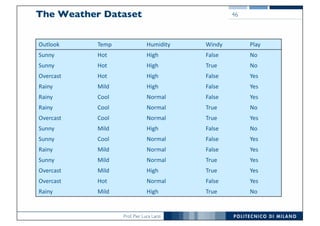
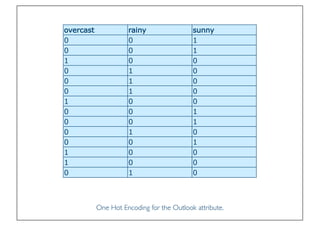
The document discusses classification and regression in data mining, outlining the process of model building and usage, particularly in contexts such as predicting contact lens recommendations based on various attributes. It covers classification algorithms, logistic regression, regularization techniques to prevent overfitting, and methods for handling categorical data, including one-hot encoding. The content also explains k-fold cross-validation for model evaluation and the extension of binary classifiers to multiclass scenarios.