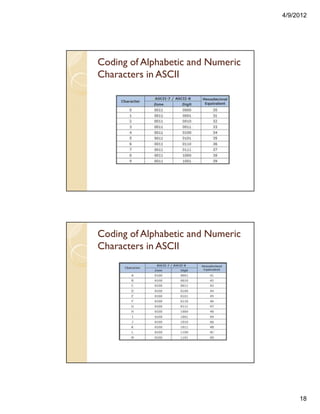
This document contains lecture notes on computer codes including BCD, EBCDIC, ASCII, and other coding systems. It discusses the binary representations of decimal digits in BCD code and provides examples of BCD addition. It also describes EBCDIC, ASCII, control codes, and the coding of alphabetic and numeric characters in these standards.

1. 4/9/2012
1
Digital Logic & Design
Dr. Sajjad Ahmed Nadeem
Department of Computer Science & IT
University of Azad Jammu & Kashmir
Muzaffarabad
Module 03
Computer Codes.
BCD.
EBCDIC.
ASCII.
Assignment-2

2. 4/9/2012
2
Data Types
Computer Codes (1)

3. 4/9/2012
3
Computer Codes (2)
Binary-Coded Decimal (BCD)
Four bits per digit Digit Bit pattern
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
Note: the following bit
patterns are not used:
1010
1011
1100
1101
1110
1111

4. 4/9/2012
4
Example
709310 = ? (in BCD)
7 0 9 3
0111 0000 1001 0011
Chapter 1 8
Warning: Conversion or Coding?
Do NOT mix up conversion of a decimal
number to a binary number with coding a
decimal number with a BINARY CODE.
1310 = 11012 (This is conversion)
13 ⇔ 0001|0011 (This is coding)

5. 4/9/2012
5
Addition-Example-1
410 0100
+510 +0101
_________________
910 1001
410 0100
+810 +1000
_________________
1100
+0110
_________________
1210 1 0010
Addition-Example-2
1 1
18410 0001 1000 0100
+57610 0101 0111 0110
______________________________________________
Binary Sum 0111 10000 1010
Add 6 0110 0110
______________________________________________
76010 0111 0110 0000

6. 4/9/2012
6
Other Decimal Codes-Binary Codes for
Decimal Digits
Decimal 8,4,2,1 Excess3 8,4,-2,-1 Gray
0 0000 0011 0000 0000
1 0001 0100 0111 0100
2 0010 0101 0110 0101
3 0011 0110 0101 0111
4 0100 0111 0100 0110
5 0101 1000 1011 0010
6 0110 1001 1010 0011
7 0111 1010 1001 0001
8 1000 1011 1000 1001
9 1001 1100 1111 1000
BCD
2421
0000
0001
0010
0011
0100
1011
1100
1101
1110
1111
Other Decimal Codes-Binary Codes for Decimal Digits
• Excess-3
• Is unweighted code
• Is obtained from the corresponding values + 3
• has been used in some older computers.
• Some digits in 2421 can be coded in two possible
ways e.g. 4 = 0100 and 4=1010

7. 4/9/2012
7
13
What special property does the Gray code
have in relation to adjacent decimal digits?
GRAY CODE – Decimal
Decimal 8,4,2,1 Gray
0 0000 0000
1 0001 0100
2 0010 0101
3 0011 0111
4 0100 0110
5 0101 0010
6 0110 0011
7 0111 0001
8 1000 1001
9 1001 1000
EBCDIC
Extended BCD Interchange Code
8-bit code (28 = 256 different characters)
Developed by IBM
Rarely used today
IBM mainframes only

8. 4/9/2012
8
Coding of Alphabetic and Numeric
Characters in EBCDIC
Coding of Alphabetic and Numeric
Characters in EBCDIC

9. 4/9/2012
9
EBCDIC
The Problem
Representing text strings, such as
“Hello, world”, in a computer

10. 4/9/2012
10
ASCII
ASCII-7 Features
7-bit code
8th bit is unused (or used for a parity bit)
27 = 128 codes
Two general types of codes:
◦ 95 are “Graphic” codes (displayable on a
console)
◦ 33 are “Control” codes (control features of
the console or communications channel)

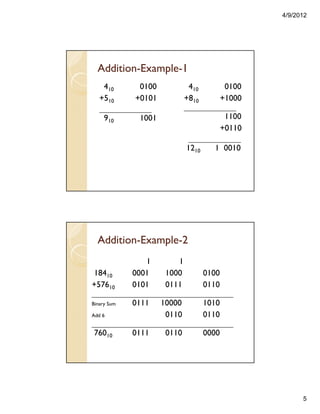
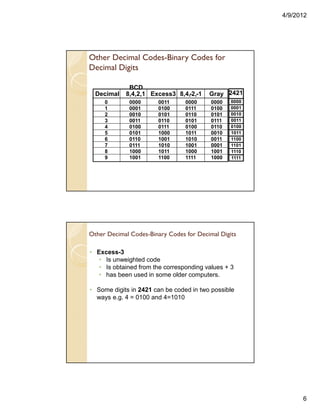
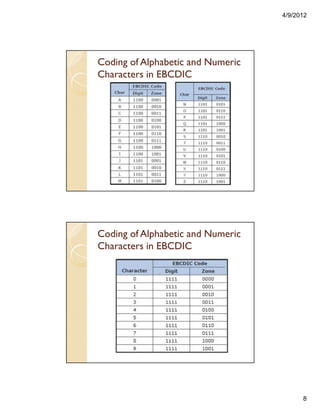
11. 4/9/2012
11
ASCII-7 Chart
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

12. 4/9/2012
12
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
Most significant bit
Least significant bit
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
e.g., ‘a’ = 1100001

13. 4/9/2012
13
95 Graphic codes
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
33 Control codes
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

14. 4/9/2012
14
Alphabetic codes
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
Numeric codes
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

15. 4/9/2012
15
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
Punctuation, etc.
“Hello, world” Example
=
=
=
=
=
=
=
=
=
=
=
=
Binary
01001000
01100101
01101100
01101100
01101111
00101100
00100000
01110111
01100111
01110010
01101100
01100100
Hexadecimal
48
65
6C
6C
6F
2C
20
77
67
72
6C
64
Decimal
72
101
108
108
111
44
32
119
103
114
108
100
H
e
l
l
o
,
w
o
r
l
d
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=

16. 4/9/2012
16
Common Control Codes
CR 0D carriage return
LF 0A line feed
HT 09 horizontal tab
DEL 7F delete
NULL 00 null
Hexadecimal code
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

17. 4/9/2012
17
Terminology
Learn the names of the special symbols
◦ [ ] brackets
◦ { } braces
◦ ( ) parentheses
◦ @ commercial ‘at’ sign
◦ & ampersand
◦ ~ tilde
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

18. 4/9/2012
18
Coding of Alphabetic and Numeric
Characters in ASCII
Coding of Alphabetic and Numeric
Characters in ASCII

19. 4/9/2012
19
Coding of Alphabetic and Numeric
Characters in ASCII
PARITY BIT Error-Detection Codes
Redundancy (e.g. extra information),in the form
of extra bits, can be incorporated into binary
code words to detect and correct errors.
A simple form of redundancy is parity, an extra
bit appended onto the code word to make the
number of 1’s odd or even. Parity can detect all
single-bit errors and some multiple-bit errors.
A code word has even parity if the number of
1’s in the code word is even.
A code word has odd parity if the number of 1’s
in the code word is odd.

20. 4/9/2012
20
4-Bit Parity Code Example
Fill in the even and odd parity bits:
The codeword "1111" has even parity and the
codeword "1110" has odd parity. Both can be
used to represent 3-bit data.
Even Parity Odd Parity
Message - Parity Message - Parity
000 - 000 -
001 - 001 -
010 - 010 -
011 - 011 -
100 - 100 -
101 - 101 -
110 - 110 -
111 - 111 -
Assignment-2
BCD subtraction
UNICODE