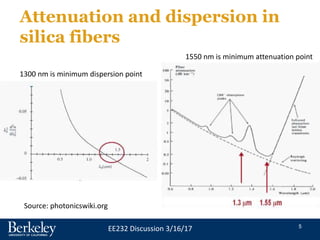
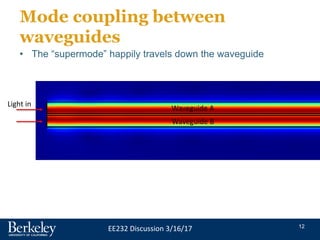
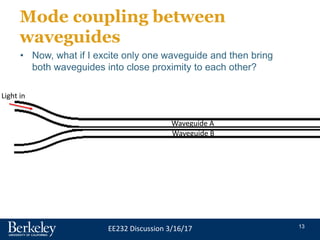
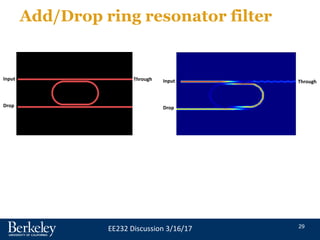
This document discusses single wavelength optical communication and wavelength division multiplexing (WDM). It then focuses on ring resonator structures, including how they can be used for filtering, modulation, and multiplexing/demultiplexing of optical signals. Key points covered include mode coupling between waveguides, using ring resonators for all-pass filtering and adding/dropping wavelengths, and exploiting the sensitivity of ring resonator resonance to index changes for modulation applications. Upcoming classes will design ring resonator-based modulators.