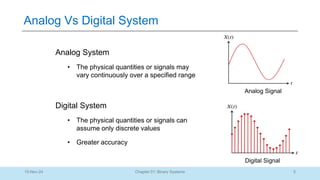
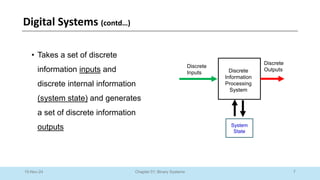
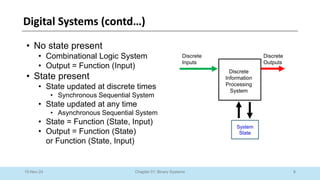
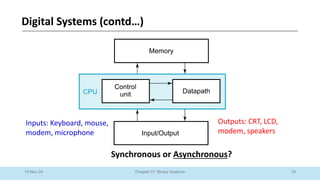
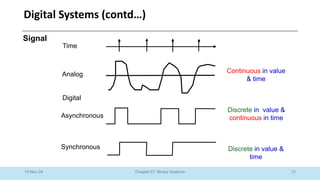
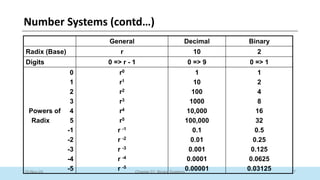
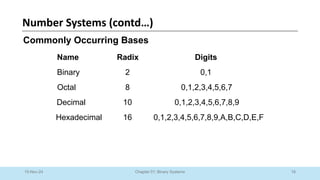
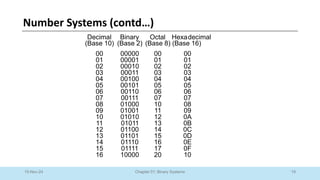
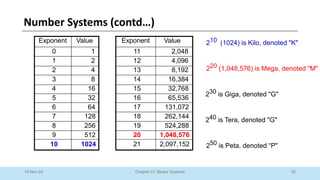
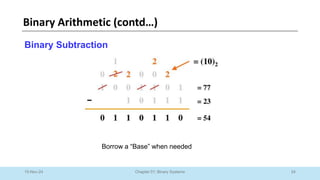
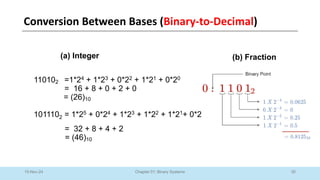
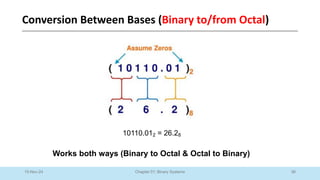
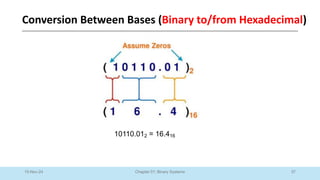
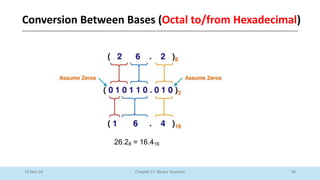
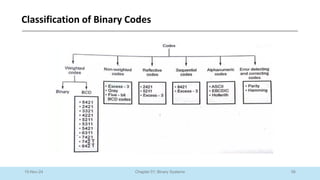
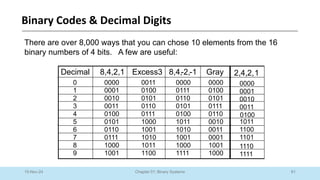
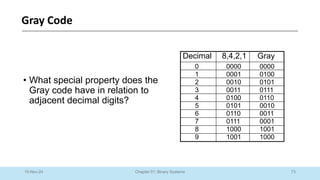
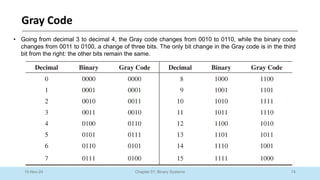
The document outlines a course on Digital Logic Design, covering binary systems, number bases, and the functioning of digital systems. It describes key concepts such as binary numbers, conversions between number systems, and binary arithmetic necessary for understanding digital electronics. The course aims to provide students with foundational knowledge applicable in various digital applications and technology.