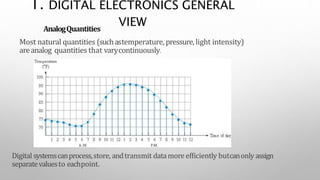
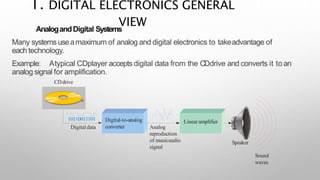
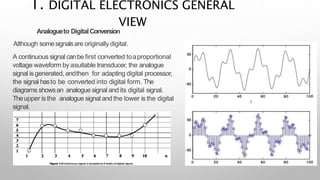
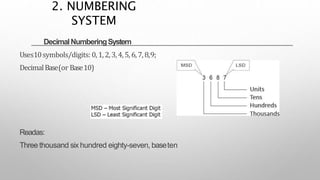
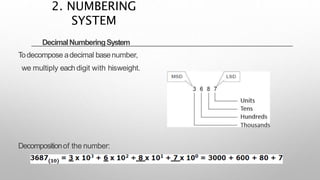
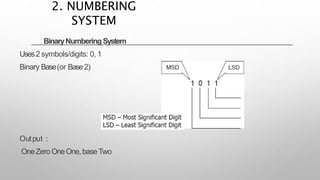
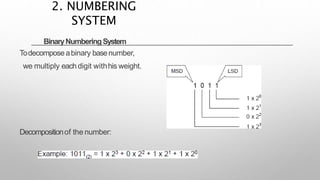
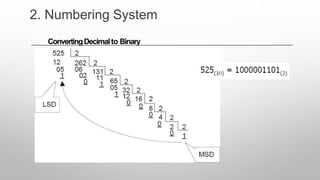
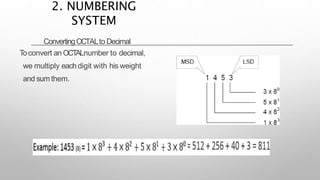
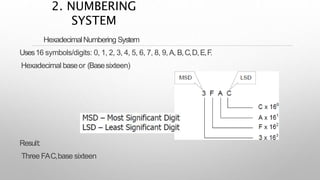
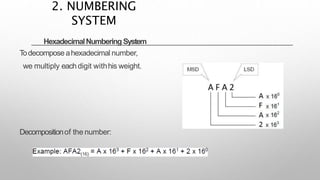
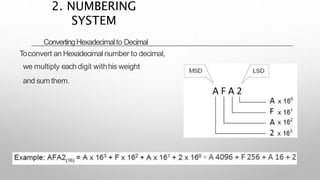
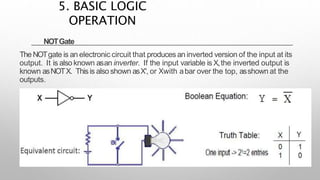
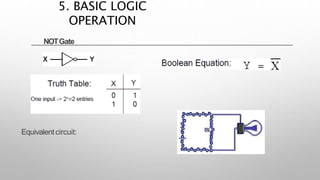
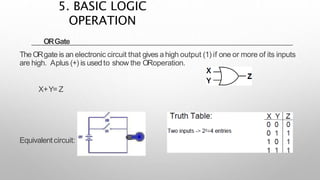
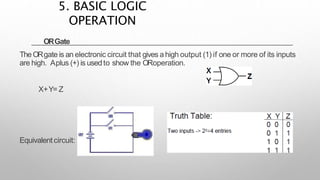
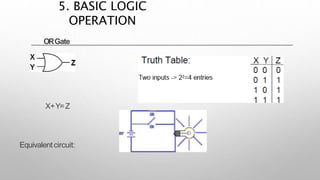
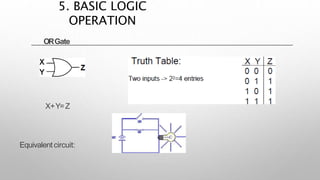
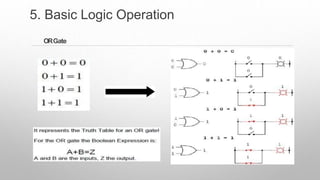
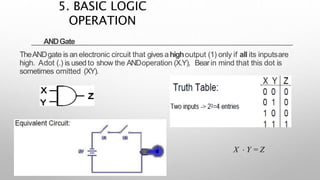
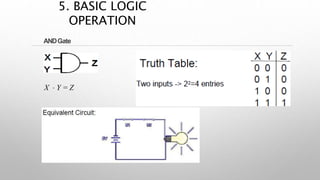
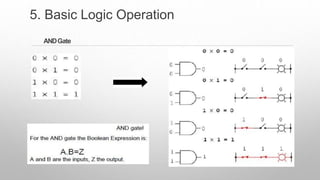
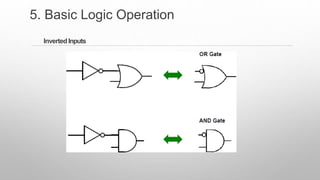
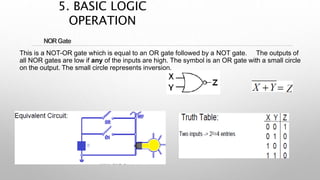
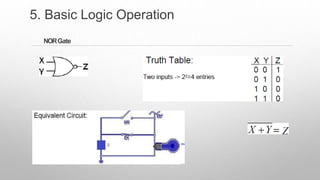
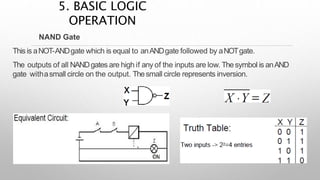
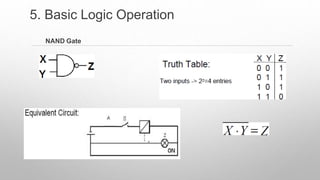
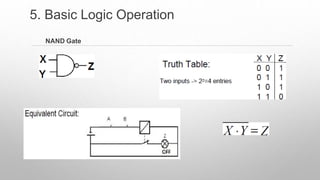
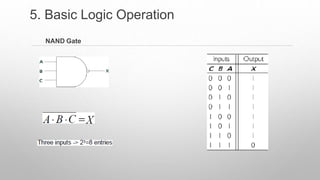
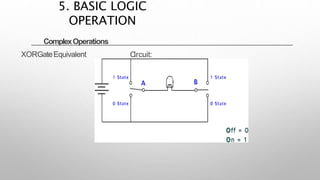
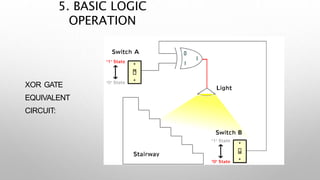
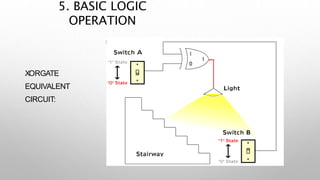
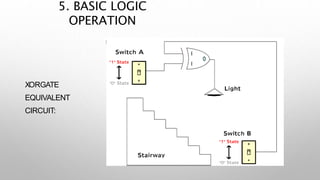
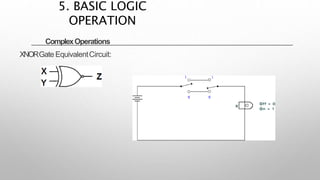
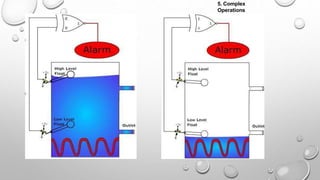
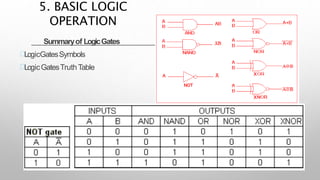
This document provides information about a digital electronics course syllabus, including: 1. The course is titled EC8392 Digital Electronics and covers topics such as digital fundamentals, combinational and sequential circuit design, memory devices, and digital integrated circuits. 2. The syllabus is divided into 5 units that cover these topics in more detail over 45 class periods. 3. The objectives of the course are to present digital fundamentals, design digital circuits, explain sequential circuits and memory technology, and introduce electronic circuit implementation.

1. EC8392 – DIGITAL ELECTRONICS
Unit1
Digital ElectronicsGeneral View
Subject Name : EC 8392 – Digital Electronics
Department : Electronics and Communication
Engineering
Class : III year ECE
Dr.M.A.Raja
Professor
ECE Department
NEHRU INSTITUTE OF ENGINEERING AND TECHNOLOGY
T. M. Palayam, Coimbatore-641 105
(Approved by AICTE, New Delhi and Affiliated to Anna UniversityChennai)
Accredited by NAAC, Recognized by UGC under Section 2(f) and 12, (B)

2. EC8392 – DIGITAL ELECTRONICS
SYLLABUS
EC8392 DIGITAL ELECTRONICS L T P C 3 0 0 3 TOTAL:45 PERIODS
OBJECTIVES:
To present the Digital fundamentals, Boolean algebra and its applications in digital systems
To familiarize with the design of various combinational digital circuits using logic gates
To introduce the analysis and design procedures for synchronous and asynchronous sequential circuits
To explain the various semiconductor memories and related technology
To introduce the electronic circuits involved in the making of logic gates
UNIT I DIGITAL FUNDAMENTALS 9
Number Systems – Decimal, Binary, Octal, Hexadecimal, 1‘s and 2‘s complements, Codes – Binary, BCD, Excess 3, Gray, Alphanumeric codes, Boolean theorems, Logic
gates, Universal gates, Sum of products and product of sums, Minterms and Maxterms, Karnaugh map Minimization and Quine-McCluskey method of minimization.
UNIT II COMBINATIONAL CIRCUIT DESIGN 9
Design of Half and Full Adders, Half and Full Subtractors, Binary Parallel Adder – Carry look ahead Adder,
BCD Adder, Multiplexer, Demultiplexer, Magnitude Comparator, Decoder, Encoder, Priority Encoder.
UNIT III SYNCHRONOUS SEQUENTIAL CIRCUITS 9
Flip flops – SR, JK, T, D, Master/Slave FF – operation and excitation tables, Triggering of FF, Analysis and
design of clocked sequential circuits – Design – Moore/Mealy models, state minimization, state assignment, circuit implementation – Design of Counters- Ripple Counters,
Ring Counters, Shift registers, Universal Shift Register.
UNIT IV ASYNCHRONOUS SEQUENTIAL CIRCUITS 9
Stable and Unstable states, output specifications, cycles and races, state reduction, race free assignments, Hazards, Essential Hazards, Pulse mode sequential circuits,
Design of Hazard free circuits.
UNIT V MEMORY DEVICES AND DIGITAL INTEGRATED CIRCUITS 9
Basic memory structure – ROM -PROM – EPROM – EEPROM –EAPROM, RAM – Static and dynamic RAM – Programmable Logic Devices – Programmable Logic Array
(PLA) – Programmable Array Logic (PAL) – Field Programmable Gate Arrays (FPGA) – Implementation of combinational logic circuits using PLA, PAL.
Digital integrated circuits: Logic levels, propagation delay, power dissipation, fan-out and fan-in, noise
margin, logic families and their characteristics-RTL, TTL, ECL, CMOS
OUTCOMES:
At the end of the course:
Use digital electronics in the present contemporary world
Design various combinational digital circuits using logic gates
Do the analysis and design procedures for synchronous and asynchronous sequential circuits
Use the semiconductor memories and related technology
Use electronic circuits involved in the design of logic gates

3. 1. DIGITAL ELECTRONICS GENERAL
VIEW
Introductionto DigitalElectronics
Digitalelectronicsisabranchof electronicswhichdealswith digitalformat of dataandcodes.
Digitalstandfor digit,digital electronicsbasicallyhastwo conditionswhicharepossible, 0
(low logic)and1(highlogic).
Digital electronic systemsuseadigital signalthat arecomposedofmathematical features to
work.
"1" astrue and"0" asfalsearecalledbit andthe groupof bitsarenamedbyte.
Digitalelectronic circuitsareusuallymadefrom largeassembliesof logicgates.
Digitaldescribeselectronic technology that generates,stores, andprocessesdata in termsof two
states:1andnumber0.
Amodemisusedto convertthe digitalinformation in yourcomputerto analogsignalsfor
your deviceandto convertanalog signalsto digital information for yourcomputer.

4. and
(ICs)
ited on
Digital ElectronicsQuick History
Priorto digital technology, electronic transmission waslimited toanalogtechnology, which
conveysdata aselectronic signalsof varyingfrequencyoramplitude.
• 1930'sthe prototypes of the computer were
constructed from mechanicalswitches(vacuum
tubes) andrelays.Thesewere comparativelyslow,
large, produced agreat dealofheat.
• Thenext stagein the 1940'swasthe useofelectronic
diodes,andwhile thesewerebetter but theywere
unreliable.
• Thenext stagewasthe result of the development in 1947
of the transistor which wasmuchsmaller,faster and
cooler.
• Simpletransistors were replacedbyintegrated
circuits andthat got smaller andsmallerand
finallydepossilicon to beput intoa"chip".
1. DIGITAL ELECTRONICS GENERAL
VIEW

5. AnalogVersusDigital
Analog=Continuouswaves
Digital =Discretewaves
Example:
Ananalogclock,whosehandsmovesmoothly andcontinuously.
Adigital clock,whosedigitsjumpfrom onevalueto the next.
1. DIGITAL ELECTRONICS GENERAL
VIEW

6. Digital systemscanprocess,store, andtransmit datamore efficiently butcanonly assign
separatevaluesto eachpoint.
1. DIGITAL ELECTRONICS GENERAL
VIEW
AnalogQuantities
Most natural quantities (suchastemperature, pressure,light intensity)
areanalog quantities that varycontinuously.

7. AnalogandDigital Systems
Many systems useamaximum of analog and digital electronics to takeadvantage of
eachtechnology.
Example: Atypical CDplayer accepts digital data from the CDdrive and converts it to an
analog signal for amplification.
CDdrive
Digital data
10110011101
Analog
reproduction
of musicaudio
signal
Speaker
Sound
waves
Digital-to-analog
converter
Linearamplifier
1. DIGITAL ELECTRONICS GENERAL
VIEW

8. 1. DIGITAL ELECTRONICS GENERAL
VIEW
Analogueto DigitalConversion
Although somesignalsare originallydigital.
A continuous signal canbe first converted toaproportional
voltage waveform by asuitable transducer, the analogue
signal is generated, andthen for adapting digital processor,
the signal hasto be converted into digital form. The
diagrams showsan analogue signal and its digital signal.
Theupper is the analogue signal and the lower is the digital
signal.

9. TheDigital Revolution
Recently, many types of devices have been converted from analog to digital.
In all of these digital devices, info is processed, transmitted and received aslong strings
of 1sand0s.
1. DIGITAL ELECTRONICS GENERAL
VIEW

10. Advantagesof Digital Electronics
• Computer-controlled digital systems canbe controlled by software, allowing
new functions to be added withoutchanging hardware.
• Information storage can be easier in digital systems than in analog ones.
• The noise-immunity of digital systems permits data to be stored and retrieved
without noise.
• In adigital system are easier to design and more precise representation of asignalcan
be obtained by using more binary digits torepresent it.
• More digital circuitry canbe fabricated onICchips.
• Error management method can be inserted into the signal path. Todetect errors,
and then either correct the errors, or at least askfor anew copy of the data.
1. DIGITAL ELECTRONICS GENERAL
VIEW

11. Disadvantagesof DigitalElectronics
Conversion to digital format and re-conversion to analog format is needed, which always
include the lost ofinformation.
In somecases,digital circuits usemore energy than analog circuits and producemore
heat and need heatsinks.
Digital circuits are sometimes moreexpensive,
especially in smallquantities.
1. DIGITAL ELECTRONICS GENERAL
VIEW

12. Unit1
NumberingSystem
EC8392 – DIGITAL
ELECTRONICS

13. Types of NumberingSystems
Manynumberingsystemsarein usein digital technology. Themost commonarethe:
Decimal 537 10
Binary 1010012
Octal 148 8
Hexadecimal 4BAF16
Toavoid confusion while using different numeral systems,
the baseof eachindividual number maybe
asspecified by writing it asasubscript of thenumber.
2. NUMBERING
SYSTEM

14. DecimalNumberingSystem
Uses10symbols/digits: 0,1,2,3,4,5,6,7,8,9;
DecimalBase(or Base10)
Readas:
Three thousand six hundred eighty-seven, baseten
2. NUMBERING
SYSTEM

15. DecimalNumberingSystem
Todecompose adecimal basenumber,
we multiply eachdigit with hisweight.
Decompositionof the number:
2. NUMBERING
SYSTEM

16. BinaryNumberingSystem
Uses2 symbols/digits: 0, 1
Binary Base(or Base2)
Output :
OneZero OneOne,baseTwo
2. NUMBERING
SYSTEM

17. BinaryNumberingSystem
Todecomposeabinary basenumber,
we multiply eachdigit withhis weight.
Decompositionof the number:
2. NUMBERING
SYSTEM

18. ConvertingDecimalto Binary
• To convert from adecimal integer numeral to binary, the number is divided by
two and the remainder is the least-significant bit(LSD).
• The result is again divided by two, and its remainder is the next least significant
bit.
• The processis repeated until theresult cannot be divided anymore and the last
result is the most-significant bit(MSD).
2. NUMBERING
SYSTEM

19. ConvertingDecimalto Binary
2. Numbering System

20. ConvertingDecimalto Binary
2. Numbering System

21. ConvertingBinaryto Decimal
Toconvert abinary number to decimal,
we multiply eachdigit withhis weight
and sumthem.
2. NUMBERING
SYSTEM

22. CONVERTING FRACTIONARY DECIMALS TO BINARY
• If it is afactionary decimal number the integer is converted using the previous
method and the factionary part is multipliedby 2;
• Theinteger part of that product is the MSDof the factionary part of the number;
• If the fractionary part is not zero, it is once more multiplied by 2 and the integer part
of that product is the next significant digit and soon until we reach zero for the
fractionary part.
2. NUMBERING
SYSTEM

23. CONVERTINGFRACTIONARYDECIMALSTOBINARY
2. Numbering System

24. BINARYCODEDDECIMALBCD
Onthe BCD(Binary CodedDecimal) system the digits aregrouped in
4 bits nibbles, eachnibble representing adecimaldigit;
Therepresentation of the decimals 10, 11, 12, 13, 14 and 15is
excluded.
TheBCDis usually usedin frequency counters, digital counters
and calculators.
2. NUMBERING
SYSTEM

25. OCTALNUMBERINGSYSTEM
Uses8 symbols/digits: 0, 1, 2, 3, 4, 5, 6,7.
OCTALBaseor (Base8)
Result:
One thousand four hundred fifty-three, base eight
2. NUMBERING
SYSTEM

26. OCTALNumberingSystem
OTCALnumbering system makesit easier torepresent binary numbers with many digits
becausean octal number represents a3 digit binarynumber:
2. NUMBERING
SYSTEM

27. OCTALNumberingSystem
Todecompose an OCT
ALnumber,
we multiply eachdigit withhis weight.
Decompositionof the number:
2. NUMBERING
SYSTEM

28. ConvertingOCTALto Decimal
Toconvert an OCT
ALnumber to decimal,
we multiply eachdigit with his weight
and sumthem.
2. NUMBERING
SYSTEM

29. DecomposingaFactionaryOCTALNumber
2. Numbering System

30. HexadecimalNumbering System
Uses16 symbols/digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,A, B,C,D,E,F
.
Hexadecimal baseor (Basesixteen)
Result:
Three FAC,base sixteen
2. NUMBERING
SYSTEM

31. HEXADECIMAL NumberingSystem
Makes it even easier torepresent large binary numbers (an hexadecimal represents a4
digit binary);
2. NUMBERING
SYSTEM

32. HexadecimalNumbering System
Todecomposeahexadecimal number,
we multiply eachdigit withhis weight.
Decompositionof the number:
2. NUMBERING
SYSTEM

33. ConvertingHexadecimalto Decimal
Toconvert an Hexadecimal number to decimal,
we multiply eachdigit withhis weight
and sumthem.
2. NUMBERING
SYSTEM

34. DecomposingaFactionaryHexadecimal Number
2. Numbering System

35. Unit1
BinarySystem Operations
EC8392 – DIGITAL
ELECTRONICS

36. • Sum
• Multiplication
• Subtraction
• Division
3. BINARY SYSTEM
OPERATIONS

37. SUM(X+Y)
3. Binary System Operations

38. MULTIPLICATION
Example:
3. BINARY SYSTEM
OPERATIONS

39. SUBTRACTION(X-Y)
3. Binary System Operations

40. DIVISION (X/Y)
No table, it is done by using the mathematical rules of multiplication and
subtraction.
3. BINARY SYSTEM
OPERATIONS

41. DIGITAL ELECTRONICS
Unit1
BooleanAlgebra

42. Introduction to BooleanAlgebra
• Much of what we will be discussing wasformalized by George Boole (1815–1864) inhis
paper An Investigation of the LawsofThought.
• Thebranch of mathematics involving digital logic is aptly named BooleanAlgebra.
• Developedto investigate the fundamental laws of the human mind ´s operations relating
to reasoning.
• Its purpose is to define symbols to represent phenomenon's that will originate more
complex mathematical expressions– Boolean Functions or BooleanExpressions;
• But unlike traditional Algebra, instead of dealing with quantities, BooleanAlgebra deals
with Logic.
• Symbolslike (+) or (x) represent logic relations between signals and pules, instead of sum
and multiplication algorithms.
• Thesymbols 0 and 1 represent LogicStates and not quantities (0 is Low or Falseand 1 is
High or True).
4. BOOLEAN
ALGEBR
A

43. Sumof TwoStates
4. Boolean Algebra

44. Productof TwoStates
Multiplication of twostates:
- There are only twopossibilities: true or false;
-Asquare wave with High value multiplying to
another results in asquare wave with Highvalue.
It doesnot matter how many or few terms we
multiply together.
4. BOOLEAN
ALGEBR
A

45. DIGITAL ELECTRONICS
Unit1
BasicLogic Operation

46. What isLogicGate?
Digital gate is aDigital Deviceusedto perform thelogic operation
Logicgates (or simply gates) are the fundamental building blocks of digital circuitry
Electronic gates require apower supply.
GateINPUTSare driven by voltages having two nominalvalues,
e.g. 0Vand 5Vrepresenting logic 0 and logic 1respectively.
TheOUTPUTof agate provides two nominal values of voltageonly,
e.g. 0Vand 5V representing logic 0 and logic 1respectively.
In general, there is only one output to alogic gate except in some special cases.
5. BASIC LOGIC
OPERATION

47. 5. BASIC LOGIC
OPERATION
TruthTable
Truth table are usedto help show the function of alogic gate.
Relation between outputs andinputs.
Number of entries on thetable is with n
being the number of entries and base2because
it is related to the binary numbering 0 and 1.

48. Typesof LogicGate
NOTGate
– Output is the invert of the input;
– Always one input.
ORGate
– Output is the binary sum of theinputs.
ANDGate
– Output is the binary multiplication of the inputs.
5. BASIC LOGIC
OPERATION

49. NOTGate
The NOTgate is an electronic circuit that produces an inverted version of the input at its
output. It is also known asan inverter. If the input variable is X,the inverted output is
known asNOTX. Thisis also shown asX', or Xwith abar over the top, asshown at the
outputs.
5. BASIC LOGIC
OPERATION

50. NOTGate
Equivalentcircuit:
5. BASIC LOGIC
OPERATION

51. NOTGate
Boolean variables are 1 or 0, and eachone hasits complement orinverse.
5. BASIC LOGIC
OPERATION

52. ORGate
The ORgate is an electronic circuit that gives ahigh output (1) if one or more of its inputs
are high. Aplus (+) is usedto show the ORoperation.
X+Y= Z
Equivalent circuit:
5. BASIC LOGIC
OPERATION

53. ORGate
The ORgate is an electronic circuit that gives ahigh output (1) if one or more of its inputs
are high. Aplus (+) is usedto show the ORoperation.
X+Y= Z
Equivalent circuit:
5. BASIC LOGIC
OPERATION

54. ORGate
X+Y=Z
Equivalent circuit:
5. BASIC LOGIC
OPERATION

55. ORGate
X+Y=Z
Equivalent circuit:
5. BASIC LOGIC
OPERATION

56. ORGate
5. Basic Logic Operation

57. ORGate
C+B+A=X
5. BASIC LOGIC
OPERATION

58. ANDGate
TheANDgate is an electronic circuit that gives ahighoutput (1) only if all its inputsare
high. Adot (.) is usedto show the ANDoperation (X.Y), Bearin mind that this dot is
sometimes omitted (XY).
X  Y = Z
5. BASIC LOGIC
OPERATION

59. ANDGate
X  Y = Z
5. BASIC LOGIC
OPERATION

60. ANDGate
5. Basic Logic Operation

61. ANDGate
5. Basic Logic Operation

62. Inverted Inputs
5. Basic Logic Operation

63. NORGate
This is a NOT-OR gate which is equal to an OR gate followed by a NOT gate. The outputs of
all NOR gates are low if any of the inputs are high. The symbol is an OR gate with a small circle
on the output. The small circle represents inversion.
5. BASIC LOGIC
OPERATION

64. NORGate
5. Basic Logic Operation

65. NORGate
5. Basic Logic Operation

66. NAND Gate
Thisis aNOT-ANDgate which is equal to anANDgate followed by aNOTgate.
The outputs of all NANDgates are high if any of the inputs are low. Thesymbol is anAND
gate withasmall circle on the output. Thesmall circle represents inversion.
5. BASIC LOGIC
OPERATION

67. NAND Gate
5. Basic Logic Operation

68. NAND Gate
5. Basic Logic Operation

69. NAND Gate
5. Basic Logic Operation

70. ComplexOperations
Upuntil now we remembered the followinglogic gates:
NOT
, OR, AND, NOR, NAND
There are two more gates available to do more complex operations:
- XOR(Exclusive-OR),and its output is HIGHonly if the number of HIGHinputs isODD.
- XNOR(Exclusive-NOR),and its output is HIGHonly if the number of HIGHinputs isEVEN.
5. BASIC LOGIC
OPERATION

71. ComplexOperations
XORGate
The 'Exclusive-OR' gate isacircuit which will give ahigh output if its two inputs are
different.
An encircled plus sign ( ) is usedto show the EORoperation.
5. BASIC LOGIC
OPERATION

72. ComplexOperations
XORGate
5. BASIC LOGIC
OPERATION

73. ComplexOperations
XORGateEquivalent Circuit:
5. BASIC LOGIC
OPERATION

74. ComplexOperations
XORGate
EquivalentCircuit:
5. BASIC LOGIC
OPERATION

75. 5. BASIC LOGIC
OPERATION
XOR GATE
EQUIVALENT
CIRCUIT:

76. s
5. BASIC LOGIC
OPERATION
XORGATE
EQUIVALENT
CIRCUIT:

77. s
5. BASIC LOGIC
OPERATION
XORGATE
EQUIVALENT
CIRCUIT:

78. ComplexOperations
XNORGate: The 'Exclusive-NOR' gate circuit does the opposite to the XORgate. It will
give a low output when its two inputs are different. The symbol is an EXORgate with a
small circle on the output. Thesmall circlerepresents inversion.
5. BASIC LOGIC
OPERATION

79. ComplexOperations
XNORGate EquivalentCircuit:
5. BASIC LOGIC
OPERATION

80. 5. Complex
Operations

81. 5. Complex
Operations

82. Simplificationof LogicCircuits
Theprevious Boolean identities and proprieties are usedto simplify complexdigital
circuits in order to obtain more direct ways of circuit implementation.
The circuit will have the samefunction but with fewer components, and consequently
more liability at alower cost ofproduction.
Like in normalAlgebra, the useof Theorems defines the way to simplify digital circuits
using BooleanAlgebra.
5. BASIC LOGIC
OPERATION

83. Simplificationof LogicCircuits
DeMorgan'sTheorems
DeMorgan wasamathematician that developedSimplification
of LogicCircuits in Booleanalgebra.
5. BASIC LOGIC
OPERATION

84. Summaryof LogicGates
LogicGatesSymbols
LogicGatesTruthTable
5. BASIC LOGIC
OPERATION