This document provides an overview of Karnaugh maps (K-maps) for simplifying Boolean functions in digital circuit design, including techniques for 2 to 5-variable K-maps and their advantages and limitations. It emphasizes the benefits of simplification, such as reduced complexity and improved circuit performance, and discusses systematic methods for obtaining simplified expressions. Additionally, it illustrates the grouping method in K-maps to minimize product terms effectively.

1. Digital Circuit
Design
18B11EC215
Lecture 8
Karnaugh Maps

2. Outline
▪ K-Map Introduction
▪ 2-variable K-maps
▪ 3-variable K-maps
▪ 4-variable K-maps
▪ 5 –variable K-maps
▪ Simplification using K-maps

3. K-Map Introduction [1,2]
• Complexity of digital logic gates that implement a Boolean function is directly related
to the complexity of Boolean expression from which the function is implemented.
• Simplification of Boolean functions leads to simpler (and usually faster) digital
circuits.
• Simplifying Boolean functions using identities is time-consuming and error-prone.
• The map method provides a simple procedure for minimizing Boolean functions.

4. Function Simplification[1,2]
▪ Why simplify?
❖ Simpler expression uses less logic gates.
❖ Thus: cheaper, less power, faster.
▪ Simplification techniques:
❖ Algebraic Simplification.
➢ simplify symbolically using theorems/postulates.
➢ requires skill but extremely open-ended.
❖ Karnaugh Maps.
➢ diagrammatic technique
➢ easy for humans (pattern-matching skills).
➢ simplified standard forms.
➢ limited to not more than 6 variables.

5. Algebraic Simplification[1,2]
▪ Algebraic simplification aims to minimise
(i) number of literals, and
(ii) number of terms

6. Algebraic Simplification
▪ Difficulty – needs good algebraic manipulation skills.
▪ Advantage – very open-ended (to your desired form!)

7. Introduction to K-maps[1,2]
▪ Systematic method to obtain simplified sum-of-products (SOPs) Boolean
expressions.
▪ Objective: Fewest possible terms/literals.
▪ Diagrammatic technique
▪ Advantage: Easy with visual aid.
▪ Disadvantage: Limited to 5 or 6 variables.

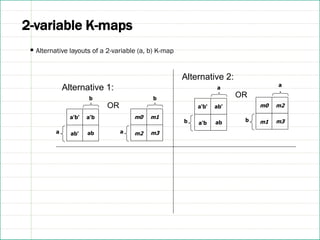
8. 2-variable K-maps[1]
▪ Karnaugh-map (K-map) is an abstract form of Venn diagram, organised as
a matrix of squares, where
❖each square represents a minterm
❖adjacent squares always differ by just one literal (so that the unifying
theorem may apply: a + a' = 1)
▪ For 2-variable case (e.g.: variables a,b), the map can be drawn as:

9. 2-variable K-maps
▪ Alternative layouts of a 2-variable (a, b) K-map
a'b' ab'
a'b ab
b
a
m0 m2
m1 m3
b
a
OR
Alternative 2:
a'b' a'b
ab' ab
a
b
m0 m1
m2 m3
a
b
Alternative 1:
OR

10. 2-variable K-maps
▪ The K-map for a function is specified by putting
❖ a ‘1’ in the square corresponding to a minterm
❖ a ‘0’ otherwise
▪ For example: Carry and Sum of a half adder.
0 0
0 1
a
b
0 1
1 0
a
b
C = ab S = ab' + a'b

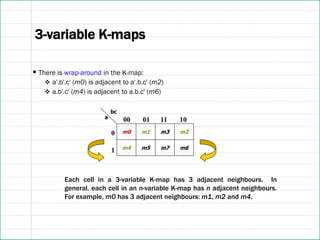
11. 3-variable K-maps[1,2]
▪ There are 8 minterms for 3 variables (a, b, c). Therefore, there are 8 cells in a 3-variable
K-map.
ab'c' ab'c
a
b
abc abc'
a'b'c' a'b'c a'bc a'bc'
0
1
00 01 11 10
c
a
bc
OR
m4 m5
a
b
m7 m6
m0 m1 m3 m2
0
1
00 01 11 10
c
a
bc
Note Gray code sequence
Above arrangement ensures that minterms of
adjacent cells differ by only ONE literal. (Other
arrangements which satisfy this criterion may also
be used.)

12. 3-variable K-maps
▪ There is wrap-around in the K-map:
❖ a'.b'.c' (m0) is adjacent to a'.b.c' (m2)
❖ a.b'.c' (m4) is adjacent to a.b.c' (m6)
m4 m5 m7 m6
m0 m1 m3 m2
0
1
00 01 11 10
a
bc
Each cell in a 3-variable K-map has 3 adjacent neighbours. In
general, each cell in an n-variable K-map has n adjacent neighbours.
For example, m0 has 3 adjacent neighbours: m1, m2 and m4.

13. 4-variable K-maps
▪ There are 16 cells in a 4-variable (w, x, y, z) K-map.
m4 m5
w
y
m7 m6
m0 m1 m3 m2
00
01
11
10
00 01 11 10
z
wx
yz
m12 m13 m15 m14
m8 m9 m11 m10
x

14. 4-variable K-maps
▪ There are 2 wrap-arounds: a horizontal wrap-around and a vertical wrap-around.
▪ Every cell thus has 4 neighbours. For example, the cell corresponding to minterm m0
has neighbours m1, m2, m4 and m8.
m4 m5
w
y
m7 m6
m0 m1 m3 m2
z
wx
yz
m12 m13 m15 m14
m8 m9 m11 m10
x

15. 5-variable K-maps
▪ Maps of more than 4 variables are more difficult to use as combining adjacent
squares becomes difficult.
▪ For 5 variables, e.g. vwxyz, need 25
= 32 squares.

16. 5-variable K-maps
Organised as two 4-variable K-maps:
Corresponding squares of each map are adjacent.
Can visualise this as being one 4-variable map on TOP of the other 4-
variable map.
m20 m21
w
y
m23 m22
m16 m17 m19 m18
00
01
11
10
00 01 11 10
z
wx
yz
m28 m29 m31 m30
m24 m25 m27 m26
x
m4 m5
w
y
m7 m6
m0 m1 m3 m2
00
01
11
10
00 01 11 10
z
wx
yz
m12 m13 m15 m14
m8 m9 m11 m10
x
v ' v

17. Larger K-maps
▪ 6-variable K-map is pushing the limit of human “pattern-recognition”
capability.
▪ K-maps larger than 6 variables are practically unheard of!

18. Simplification Using K-maps
▪ Based on the Unifying Theorem:
A + A' = 1
▪ In a K-map, each cell containing a ‘1’ corresponds to a minterm of a given
function F.
▪ Each group of adjacent cells containing ‘1’ (group must have size in powers of
twos: 1, 2, 4, 8, …) then corresponds to a simpler product term of F.
▪ Grouping 2 adjacent squares eliminates 1 variable, grouping 4 squares
eliminates 2 variables, grouping 8 squares eliminates 3 variables, and so on.
In general, grouping 2n squares eliminates n variables.

19. Simplification Using K-maps
▪ Group as many squares as possible.
❖The larger the group is, the fewer the number of literals in the resulting
product term.
▪ Select as few groups as possible to cover all the squares (minterms) of the
function.
❖The fewer the groups, the fewer the number of product terms in the
minimized function.

20. Example
• Simplify the Boolean function:
F(a, b, c) = ∑(0, 2, 4, 5, 6)
F = c’ + ab’
1 1
a
b
1
1 1
0
1
00 01 11 10
c
a
bc

21. Example
The function can be expressed in sum of minterms form:
F(a,b,c) = ∑(1, 2, 3,5,7)
F = c +a’b
1
a
b
1
1 1 1
0
1
00 01 11 10
c
a
bc

22. Simplification Using K-maps
▪ Example:
F (w, x, y, z) =  m(4, 5, 10, 11, 14, 15)
z
1 1
w
y
00
01
11
10
00 01 11 10
wx
yz
1 1
1 1
x (cells with ‘0’ are not
shown for clarity)

23. Simplification Using K-maps
▪ Each group of adjacent minterms (group size in powers of twos) corresponds
to a possible product term of the given function.
1 1
w
00
01
11
10
00 01 11 10
z
wx
yz
1 1
1 1
x
A
B
y

24. Simplification Using K-maps
▪ There are 2 groups of minterms: A and B, where:
A = w'.x.y'.z' + w‘.x.y'.z
= w'.x.y'.(z' + z)
= w'.x.y'
B = w.x'.y.z' + w.x'.y.z + w.x.y.z' + w.x.y.z
= w.x'.y.(z' + z) + w.x.y.(z' + z)
= w.x'.y + w.x.y
= w.(x'+x).y
= w.y
1 1
w
00
01
11
10
00 01 11 10
z
wx
yz
1 1
1 1
x
A
B
y

25. Simplification Using K-maps
▪ Each product term of a group, w'.x.y' and w.y, represents the sum of minterms in that
group.
▪ Boolean function is therefore the sum of product terms (SOP) which represent all groups
of the minterms of the function.
F(w,x,y,z) = A + B = w'.x.y' + w.y

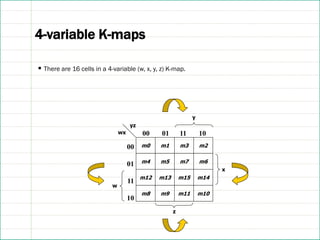
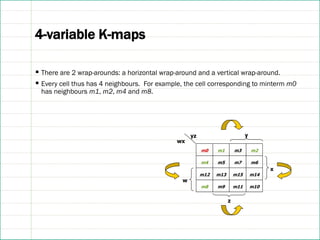
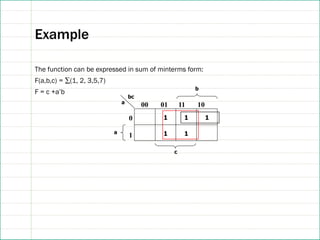
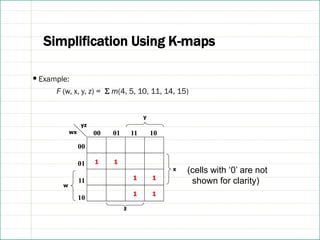
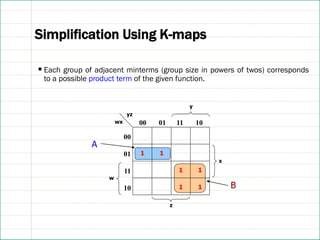
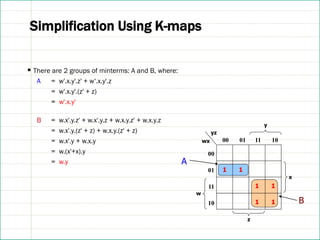
26. References
[1]. M. M. Mano, Digital logic and computer design, 5th ed., Pearson Prentice Hall, 2013.
[2]. M. M. Mano and M. D. Ciletti, Digital design, 5th ed., Pearson Prentice Hall, 2013.