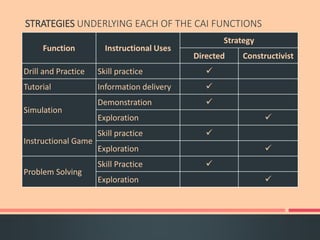
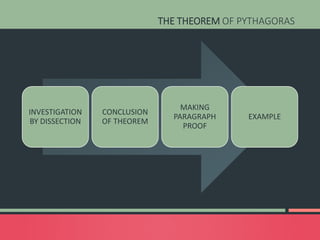
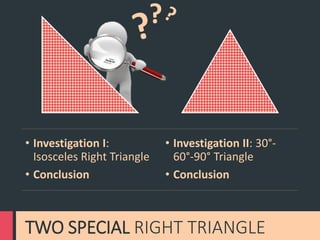
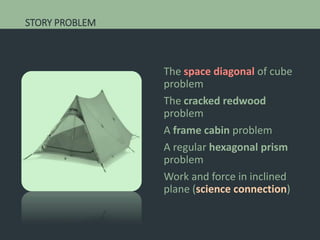
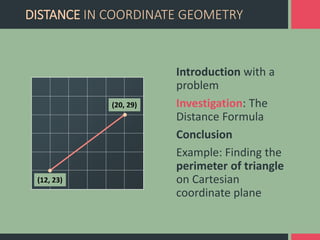
The document discusses developing a computer assisted instruction program focused on teaching the Pythagorean theorem using an investigative approach. It outlines strategies for teaching key topics related to the Pythagorean theorem through exploration and problem solving using different types of computer assisted instruction like drill and practice, tutorials, simulations, and instructional games. The document also discusses advantages and disadvantages of using computer assisted instruction and provides examples of investigations and activities that could be included in the program.

1. DEVELOPING COMPUTER ASSISTED
INSTRUCTION IN THE PYTHAGOREAN
THEOREM TOPIC WITHIN INVESTIGATIVE
APPROACH
Written by Yosep Dwi K.

2. INVESTIGATIVE APPROACH
The essence of an investigative
approach is the application of
communication, reasoning,
operational and recording processes
to a study of the core topics which
make up the content of a
mathematics curriculum.–Frobisher (1994)

3. TEACHERS’ ACTION
Demonstrate how to approach
various aspects of the
investigative processes.
Become the socializing force in
helping pupils become
mathematically literate by
encouraging them to question,
to challenge and learn
anything about the real
mathematical behavior

4. Listen to pupils so that
teachers can understand
pupils' beliefs about
learning, the experiences
they bring to specific
inquiries, and to gain
insight into the meanings
and connections pupils
construct during inquiries.
Initially give children
'short' investigations
which provide short term
rewards.

5. PUPILS’ ACTION
Become active members of a
community of practice who share
the responsibility of planning,
conducting and reflecting on
their inquiries with other
members;
Listen and negotiate with others;
and
Must have mutual trust between
peers and the teacher so that
mathematical thinking is shared
freely.

6. COMPUTER ASSISTED
INSTRUCTION

7. WHAT IS IT?
A teaching tool that involves the use of a
computer program or programs to facilitate
the education of a group of students.
(www.questia.com)
Instruction or remediation presented on a
computer. (www.readingrockets.org)
A kind of tutorial implication in which a
computer helps the learner(s) to present
material and acts a tutor. Using a branching
model of lessons in this process, the computer
presents information, asks questions, and
gives feedback. (Konukman, 2003)

8. TYPES
OF CAI
Drill and Practice
Tutorial
Simulation
Instructional Game
Problem Solving

9. STRATEGIES UNDERLYING EACH OF THE CAI FUNCTIONS
Function Instructional Uses
Strategy
Directed Constructivist
Drill and Practice Skill practice 
Tutorial Information delivery 
Simulation
Demonstration 
Exploration 
Instructional Game
Skill practice 
Exploration 
Problem Solving
Skill Practice 
Exploration 

10. 

ADVANTAGES AND DISADVANTAGES
The student can choose his own
way and speed.
The program can be stopped at
any time.
The program can be repeated as
often as the usher wishes.
The computer is not judgmental.
The student can learn from his
mistakes without embarrassment.
Saves time for the teacher (in the
long term).
The students are more activated.
Weak students are favored.
Starting costs are
high.
The staff needs to
be trained.
Students have to be
familiarized with
the medium.

11. PROTOTYPE
The Theorem of
Pythagoras
The Converse of
Pythagorean
Theorem
Two Special Right
Triangles
Story Problems
Distance in
Coordinate
Geometry

12. THE THEOREM OF PYTHAGORAS
INVESTIGATION
BY DISSECTION
CONCLUSION
OF THEOREM
MAKING
PARAGRAPH
PROOF
EXAMPLE

13. THE CONVERSE OF PYTHAGOREAN THEOREM
Investigation: Is the
Converse True?
Conclusion of the
Converse
Developing Proof
Algebra Connection:
Radical Expressions

14. • Investigation I:
Isosceles Right Triangle
• Conclusion
• Investigation II: 30°-
60°-90° Triangle
• Conclusion
TWO SPECIAL RIGHT TRIANGLE
?

15. The space diagonal of cube
problem
The cracked redwood
problem
A frame cabin problem
A regular hexagonal prism
problem
Work and force in inclined
plane (science connection)
STORY PROBLEM

16. Introduction with a
problem
Investigation: The
Distance Formula
Conclusion
Example: Finding the
perimeter of triangle
on Cartesian
coordinate plane
DISTANCE IN COORDINATE GEOMETRY
(12, 23)
(20, 29)

17. PREVIEW