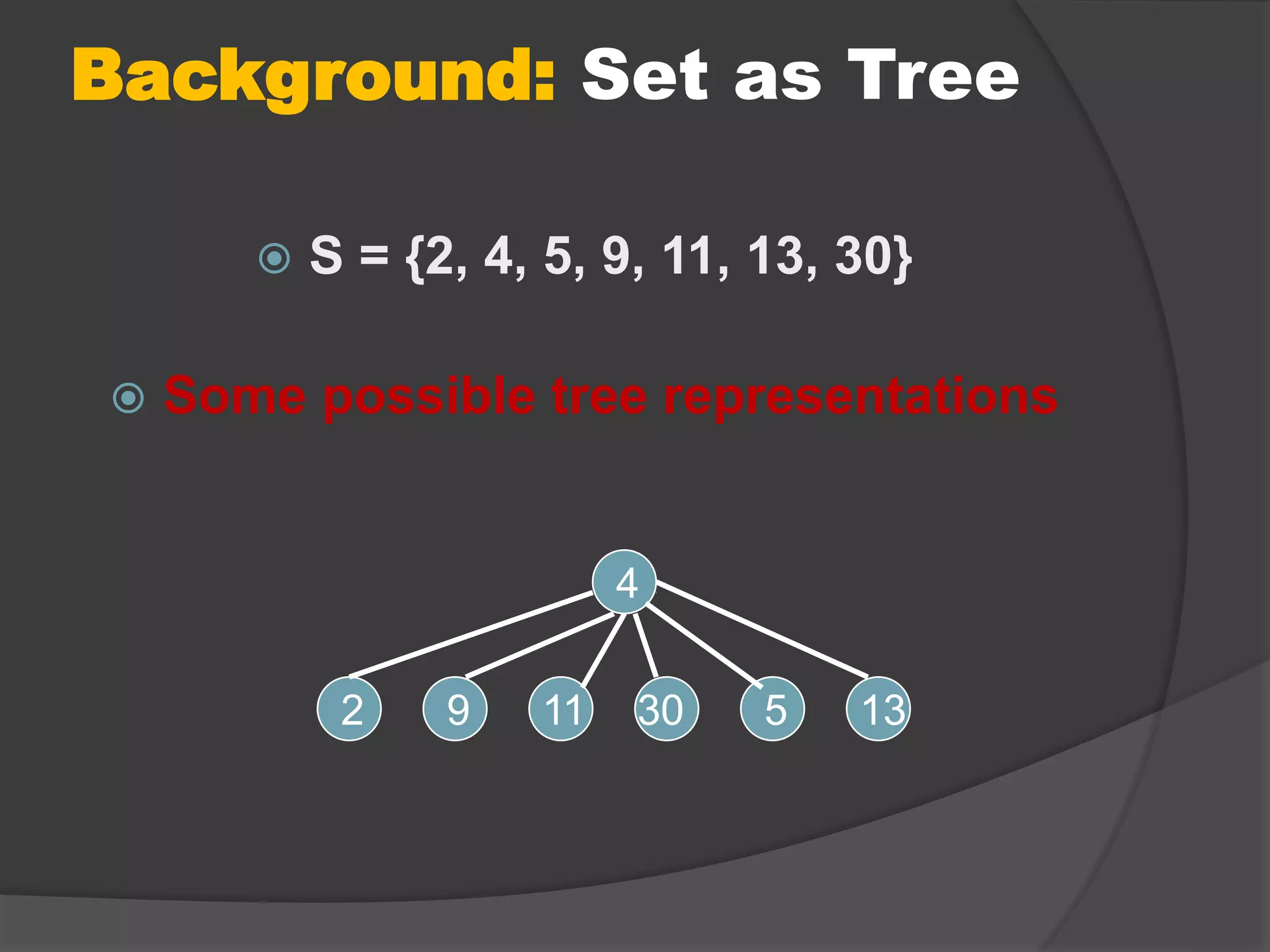
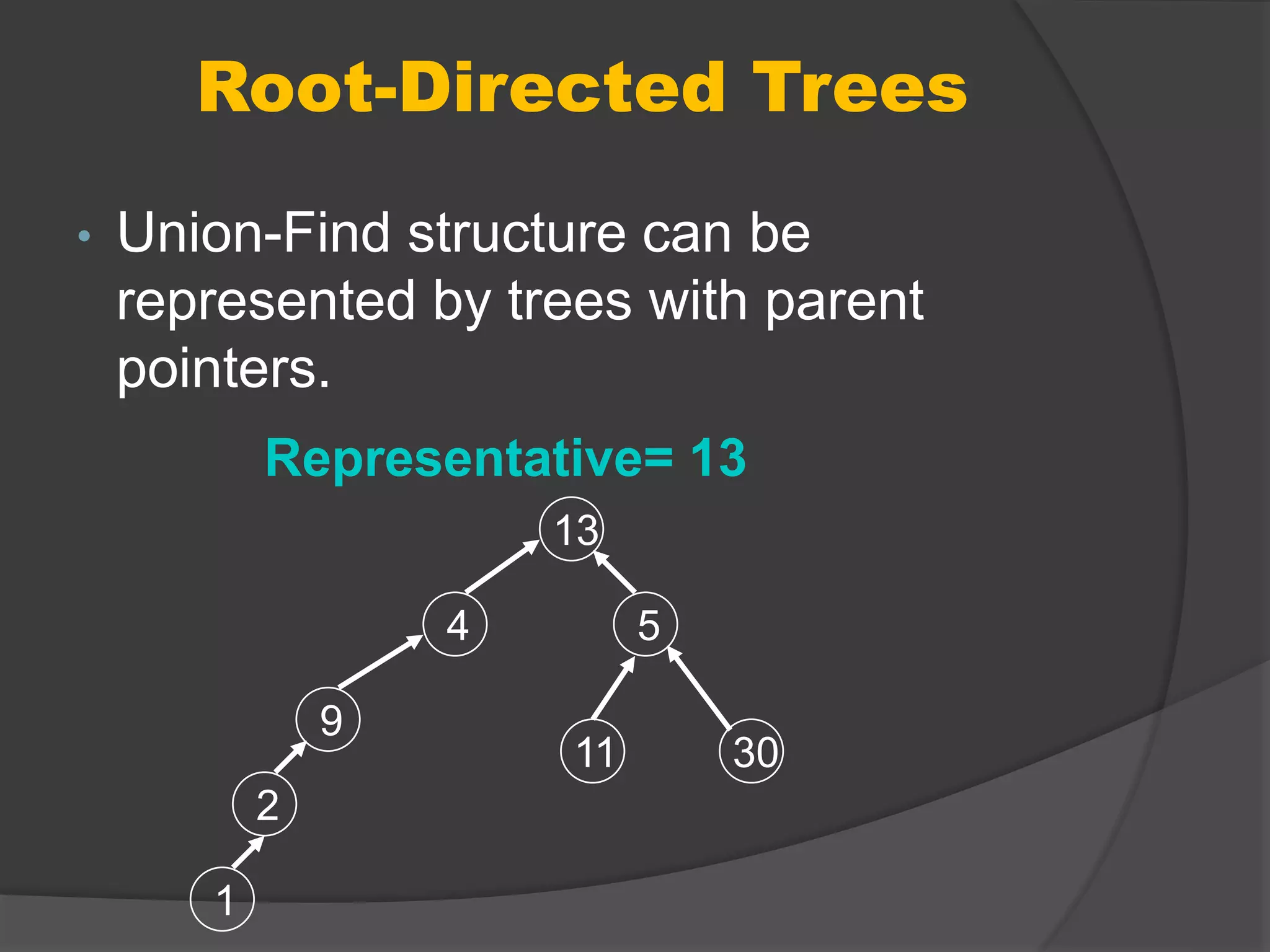
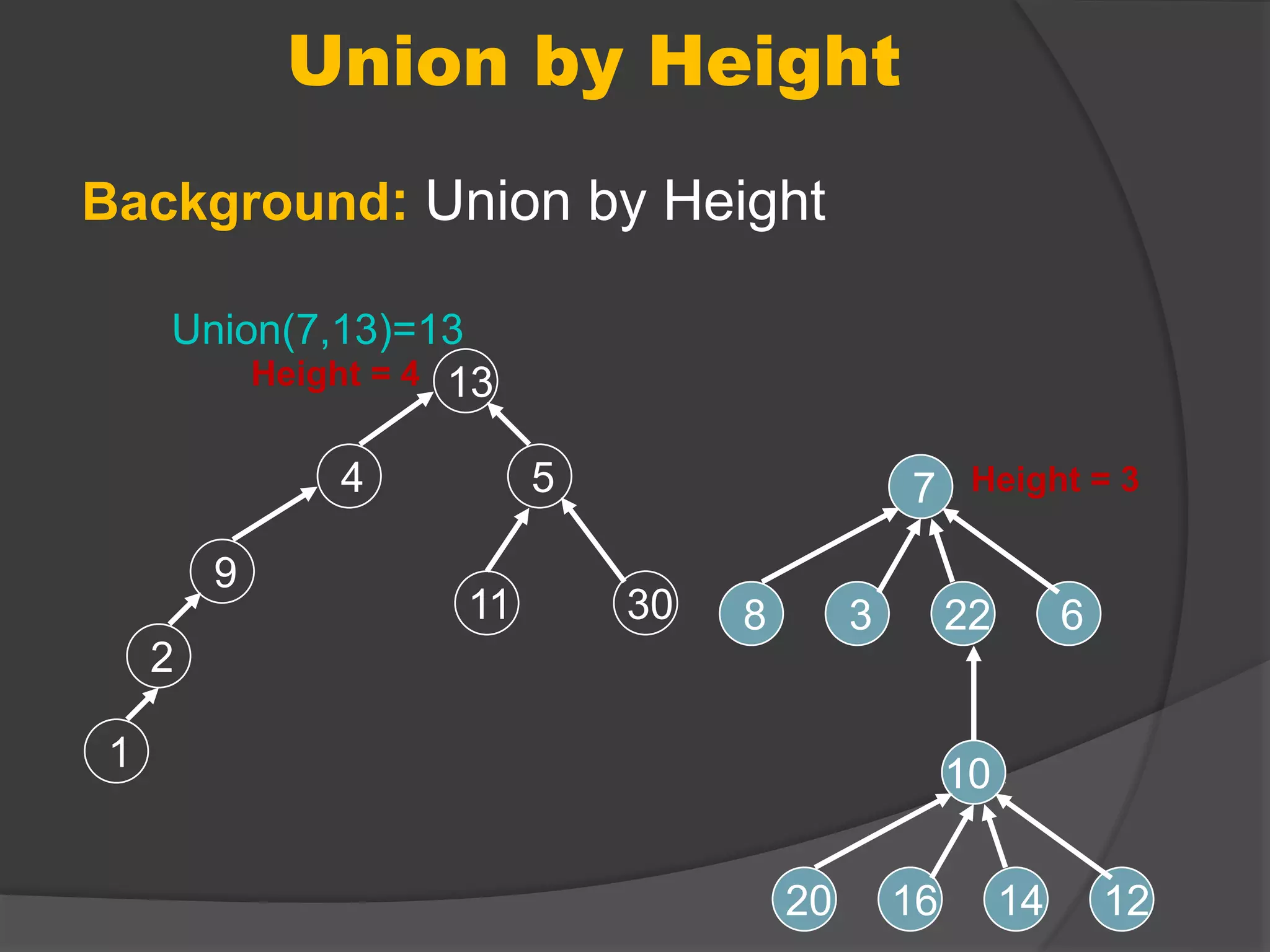
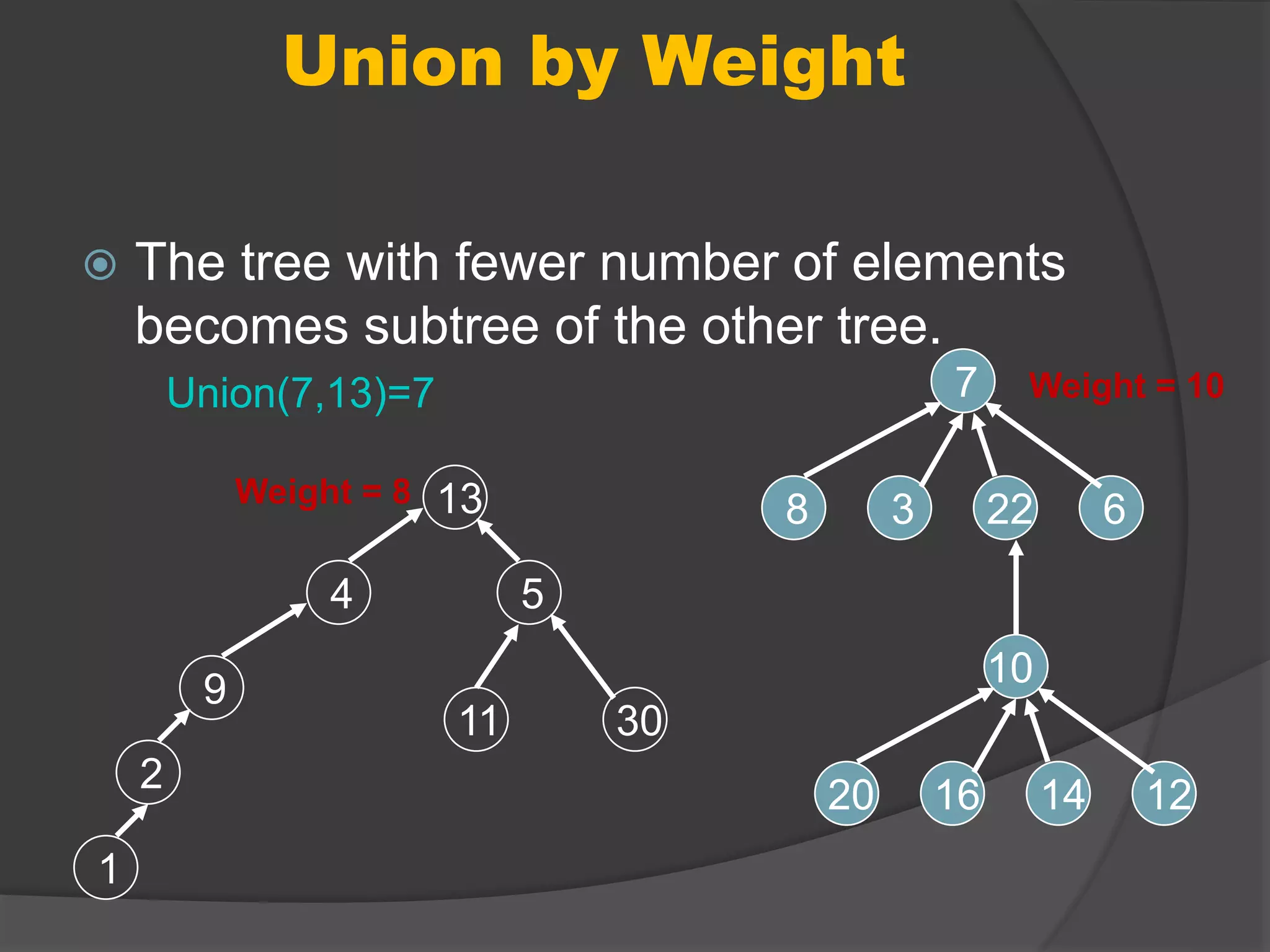
This document discusses path compression for a disjoint-set data structure, which represents sets as trees. It describes the union-find operations of find, union, and makeset. Union by rank and path compression are introduced, where ranks represent tree heights and path compression flattens trees during finds. Very quickly growing inverse functions are used to prove the amortized time of union-find with path compression is O(mα(n)), where α(n) is a very slowly growing function.

1. PATH COMPRESSION

2. Outline
 Background
 Union-Find: Merging Classes of a
Partition
 Union-Find with Copies and Dynamic
Segment Trees
 List Splitting
 Problems on Root-Directed Trees
 Maintaining a Linear Order

3. Union Whom?
&
Find What?

4. Background: Disjoint Data
Set
 Disjoint-set data structure is a data
structure that keeps track of a set of
elements partitioned into a number of
disjoint (non-overlapping) subsets.
Disjoint-set data structure is sometimes
called a union-find data structure.

5.  Union-find algorithm is an algorithm
that performs three useful operations on
such a data structure:
• Find: determine which subset a
particular element is in. This can be used
for determining if two elements are in the
same subset.
• Union: join two subsets into a single
subset.
• Makeset: makes a set containing only a
given element (a singleton).

6. Background: Set as Tree
 S = {2, 4, 5, 9, 11, 13, 30}
 Some possible tree representations
4
2 9 11 30 5 13

7. Root-Directed Trees
• Union-Find structure can be
represented by trees with parent
pointers.
Representative= 13
4
2
9
30
5
13
11
1

8. Union Operation
 Union(i,j) : i and j are the roots of two
different trees, i != j.
 To unite the trees, make one tree a
subtree of the other.
 Time Complexity of Union operation is
O(1)

9. Smart Union Approaches
There are two approaches to apply union
operation:
 Union by Height
 Union by Weight

10. Union by Height
Background: Union by Height
Union(7,13)=13
4
2
9
30
5
13
11
1
7
8 3 22 6
10
20 16 14 12
Height = 4
Height = 3

11. Union by Weight
 The tree with fewer number of elements
becomes subtree of the other tree.
4
2
9
30
5
13
11
1
7
8 3 22 6
10
20 16 14 12
Weight = 10
Weight = 8
Union(7,13)=7

12. Applications
There are many applications that utilize
this structure. Some of them are:
 Check the network connectivity.
 Kruskal's minimum spanning tree
algorithm.
 Find least common ancestor.

13. Union by Rank & Path
Compression
 Union by Rank: Each node is associated
with a rank, which is the upper bound on
the height of the node (i.e., the height of
subtree rooted at the node), then when
UNION, let the root with smaller rank
point to the root with larger rank.
 Path Compression: used in FIND-
SET(x) operation, make each node in
the path from x to the root directly point
to the root. Thus reduce the tree height.

14. Analysis of Union by Rank
with Path Compression
 Discuss the following:
 A very quickly growing function and its
very slowly growing inverse
 Properties of Ranks
 Proving time bound of O(m(n))
where (n) is a very slowly growing
function.

15.  For integers k0 and j 1, define Ak(j):
 Ak(j)= j+1 if k=0
 Ak-1
(j+1)(j) if k1
 Where Ak-1
0(j)=j, Ak-1
(i)(j)= Ak-1(Ak-1
(i-1)(j)) for i
1.
 k is called the level of the function and
 i in the above is called iterations.
 Ak(j) strictly increase with both j and k.
 Let us see how quick the increase is!!

16. Summary
 Disjoint set
 Three operations
 Different implementations and different
costs
 Forest implementation:
 Union by rank and path compression
 Properties: rank, level, iter.
 Amortized analysis of the operations:
Potential function.