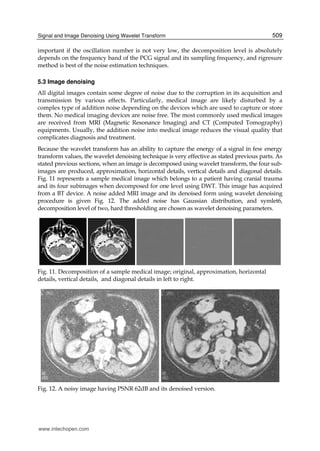
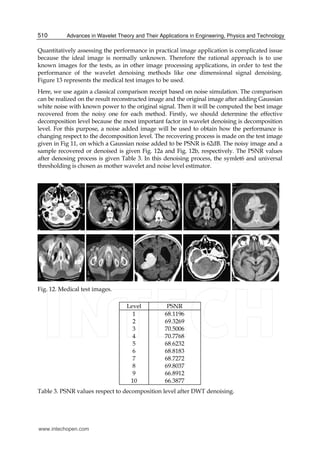
This document discusses wavelet transforms and their application to signal and image denoising. It begins with an introduction to wavelets and their advantages over Fourier transforms for analyzing non-stationary signals. It then describes discrete wavelet transforms (DWT) and wavelet packet decomposition, which decompose signals into approximation and detail coefficients. Thresholding techniques are discussed for removing noise by eliminating small wavelet coefficients assumed to represent noise. The document focuses on using DWT and thresholding to reconstruct original signals and images from noisy versions by removing noise in the high frequency detail coefficients.








![Signal and Image Denoising Using Wavelet Transform 503
Where Sure is defined as
2
( , ) 2 : min( ,i iSure X n i X X (13)
Where the operator ( ) returns the cardinality of the set : ii X , it is found that Sure is
an un biased estimate of the 2
l risk .
5. Denoising application examples
5.1 Comparison assessments
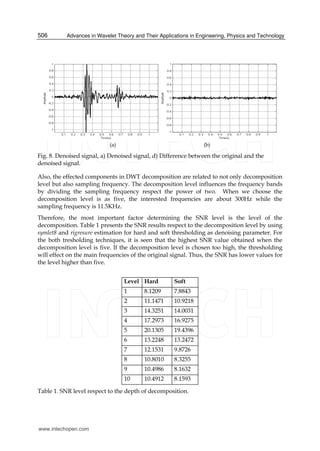
The best way to test the effect of noise on a signal is to add a Gaussian white noise, in which
case its values independently and identically distributed (i.i.d) Gaussian real values. After
the denoising process, the performance can be measure by comparing the denoised signal
and the original signal. However, many methods have been proposed to measure the
performance of denoising algorithms, the signal to noise ratio (SNR) and peak signal to
noise ratio (PSNR) has generally accepted to measure the quality of signal and images,
respectively. For one dimensional signal, measuring the performance of the denoising
method by calculation of the residual SNR given as;
1 1 2
2
10
0 0
10log ( ) ( ) ( ])r
N N
n n
SNR x n x n x n
(14)
where ( )x n is the original signal, ( )rx n is the denoised signal and ( )x n refers to the mean
value of ( )x n .
In order to measure the quality of image, it is generally used PSNR, which given as;
1 1 2
10
0 0
10log ( , ) ( , )r
N M
n m
PSNR L x n m x n m
(15)
where L denotes the quantized gray level of the images, ( )x n is original images, ( , )x n m is
the mean value of ( )x n , and ( , )r
x n m refers to reconstructed image. In order to get visible
alteration on signal, the power of noise should be chosen adequately. Indeed, SNR is usually
the most important measure rather than the power of noise, when taking into consideration
that the power of the signal to denoise can be varied. When the SNR is chosen above 3dB, it
is generally enough to get the visible corruption.
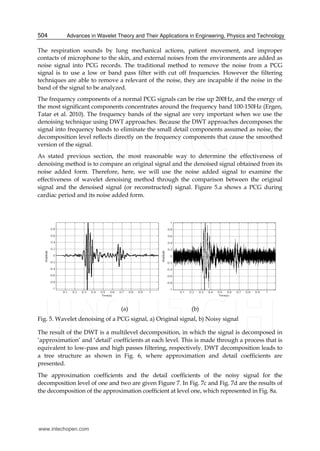
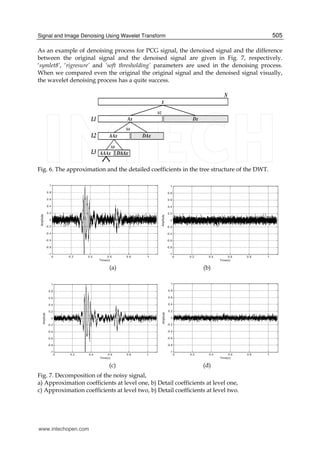
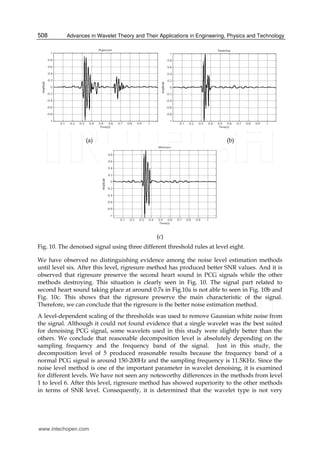
5.2 Phonocardiogram denoising
The records of the acoustical vibrations produced by heart, acquired through microphones
from human chest, called phonocardiogram (PCG), consist of the heart sounds and the
murmurs. This records of acoustic signals are unfortunately disturbed by various factors
which effecting as noise. These effects decrease the performance of visual and computerized
analysis (Akay, Semmlow et al. 1990; Ergen, Tatar et al. 2010).
www.intechopen.com](https://image.slidesharecdn.com/34967-160128141239/85/34967-9-320.jpg)


![Signal and Image Denoising Using Wavelet Transform 513
Jiang, Q. (1998). "Orthogonal multiwavelets with optimum time-frequency resolution."
Signal Processing, IEEE Transactions on 46(4): 830-844.
Jovanov, L., A. Pi urica, et al. (2010). "Fuzzy logic-based approach to wavelet denoising of
3D images produced by time-of-flight cameras." Optics Express 18(22): 22651-
22676.
Lang, M., H. Guo, et al. (1996). "Noise reduction using an undecimated discrete wavelet
transform." Signal Processing Letters, IEEE 3(1): 10-12.
Lewis, A. S. and G. Knowles (1992). "Image compression using the 2-D wavelet transform."
Image Processing, IEEE Transactions on 1(2): 244-250.
Mallat, S. and Z. Zhang (1993). "Matching pursuits with time-frequency dictionaries." IEEE
Transactions on signal processing 41(12): 3397-3415.
Mallat, S. G. (1989). "A theory for multiresolution signal decomposition: The wavelet
representation." Pattern Analysis and Machine Intelligence, IEEE Transactions on
11(7): 674-693.
Mallat, S. G. (1999). A wavelet tour of signal processing, Academic Pr.
Meyer, F., A. Averbuch, et al. (2002). "Fast adaptive wavelet packet image compression."
Image Processing, IEEE Transactions on 9(5): 792-800.
Misiti, M., Y. Misiti, et al. "Wavelet Toolbox(tm) 4." Matlab User's Guide, Mathworks.
Moulin, P. and J. Liu (1999). "Analysis of multiresolution image denoising schemes using
generalized Gaussian and complexity priors." Information Theory, IEEE
Transactions on 45(3): 909-919.
Nasri, M. and H. Nezamabadi-pour (2009). "Image denoising in the wavelet domain using a
new adaptive thresholding function." Neurocomputing 72(4-6): 1012-1025.
Pizurica, A., A. M. Wink, et al. (2006). "A review of wavelet denoising in MRI and
ultrasound brain imaging." Current Medical Imaging Reviews 2(2): 247-260.
Portilla, J., V. Strela, et al. (2003). "Image denoising using scale mixtures of Gaussians in the
wavelet domain." Image Processing, IEEE Transactions on 12(11): 1338-1351.
Qian, S. and D. Chen (1999). "Joint time-frequency analysis." Signal Processing Magazine,
IEEE 16(2): 52-67.
Qu, Y., B. Adam, et al. (2003). "Data reduction using a discrete wavelet transform in
discriminant analysis of very high dimensionality data." Biometrics 59(1): 143-151.
Rioul, O. and M. Vetterli (1991). "Wavelets and signal processing." Signal Processing
Magazine, IEEE 8(4): 14-38.
Sen, O., S. Zhengxiang, et al. (2002). "Application of wavelet soft-threshold de-noising
technique to power quality detection [J]." Automation of Electric Power Systems 19.
Simoncelli, E. P. and E. H. Adelson (1996). Noise removal via Bayesian wavelet coring, IEEE.
Valens, C. "A Really Friendly Guide to Wavelets. 1999." URL: http://perso. orange. fr
/polyvalens/ clemens/ wavelets/ wavelets. html [Last accessed: 13 December
2007].
Vetterli, M. and C. Herley (1992). "Wavelets and filter banks: Theory and design." Signal
Processing, IEEE Transactions on 40(9): 2207-2232.
Vetterli, M. and J. Kova evi (1995). Wavelets and subband coding, Citeseer.
Vetterli, M. and J. Kovacevic (1995). Wavelets and Subband Coding. Englewood Clis, NJ:
Prentice-Hall.
www.intechopen.com](https://image.slidesharecdn.com/34967-160128141239/85/34967-19-320.jpg)

