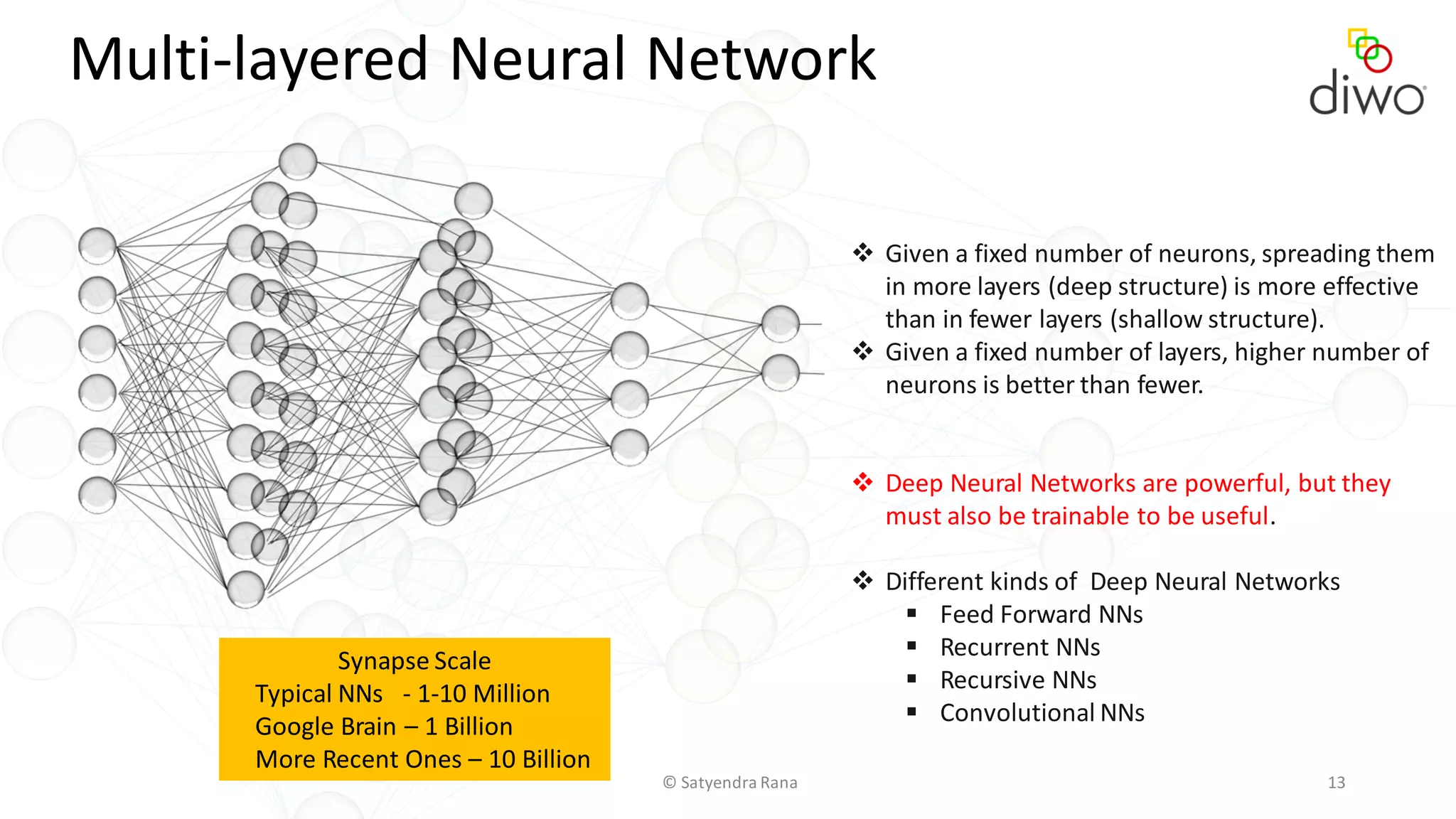
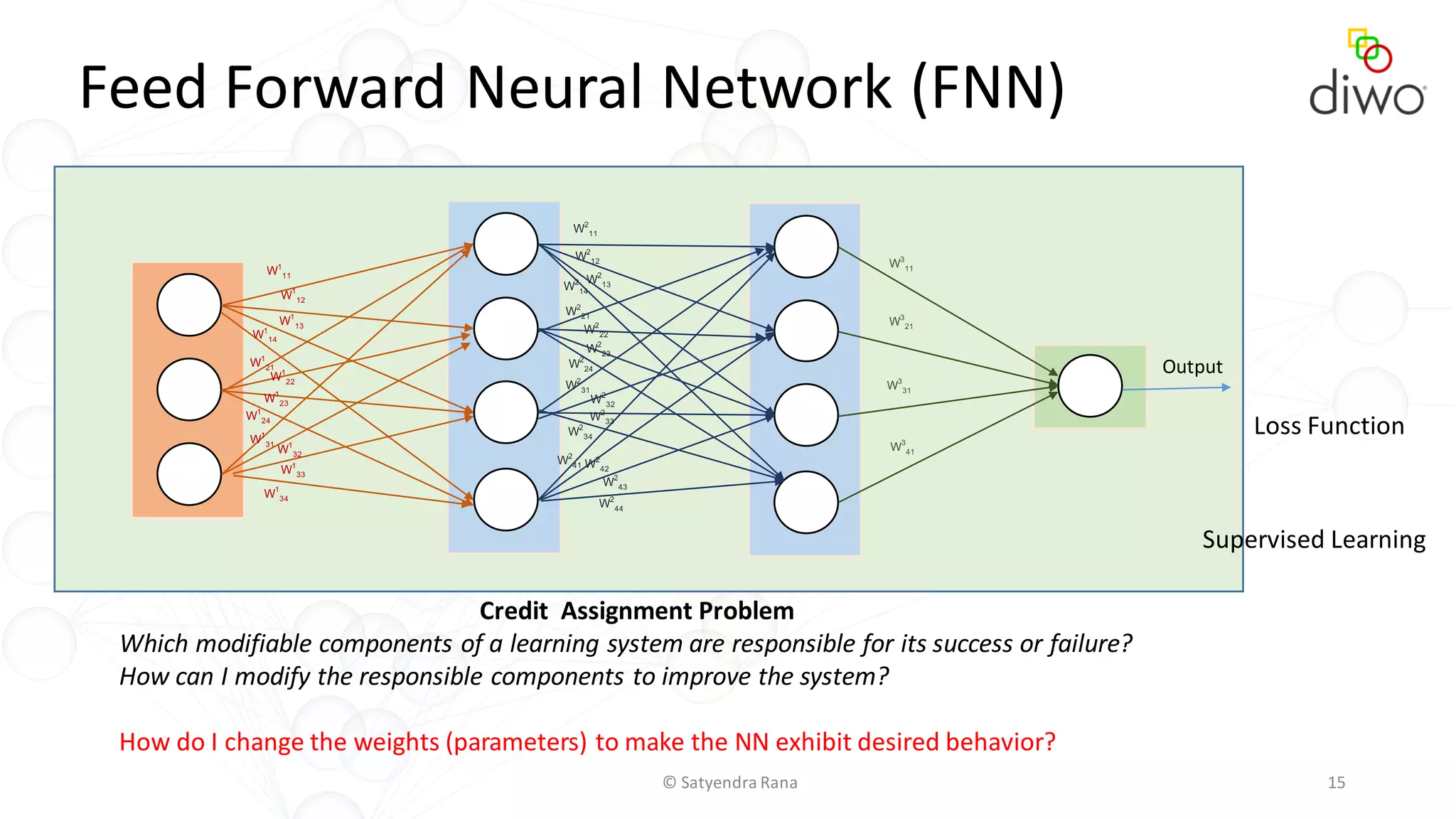
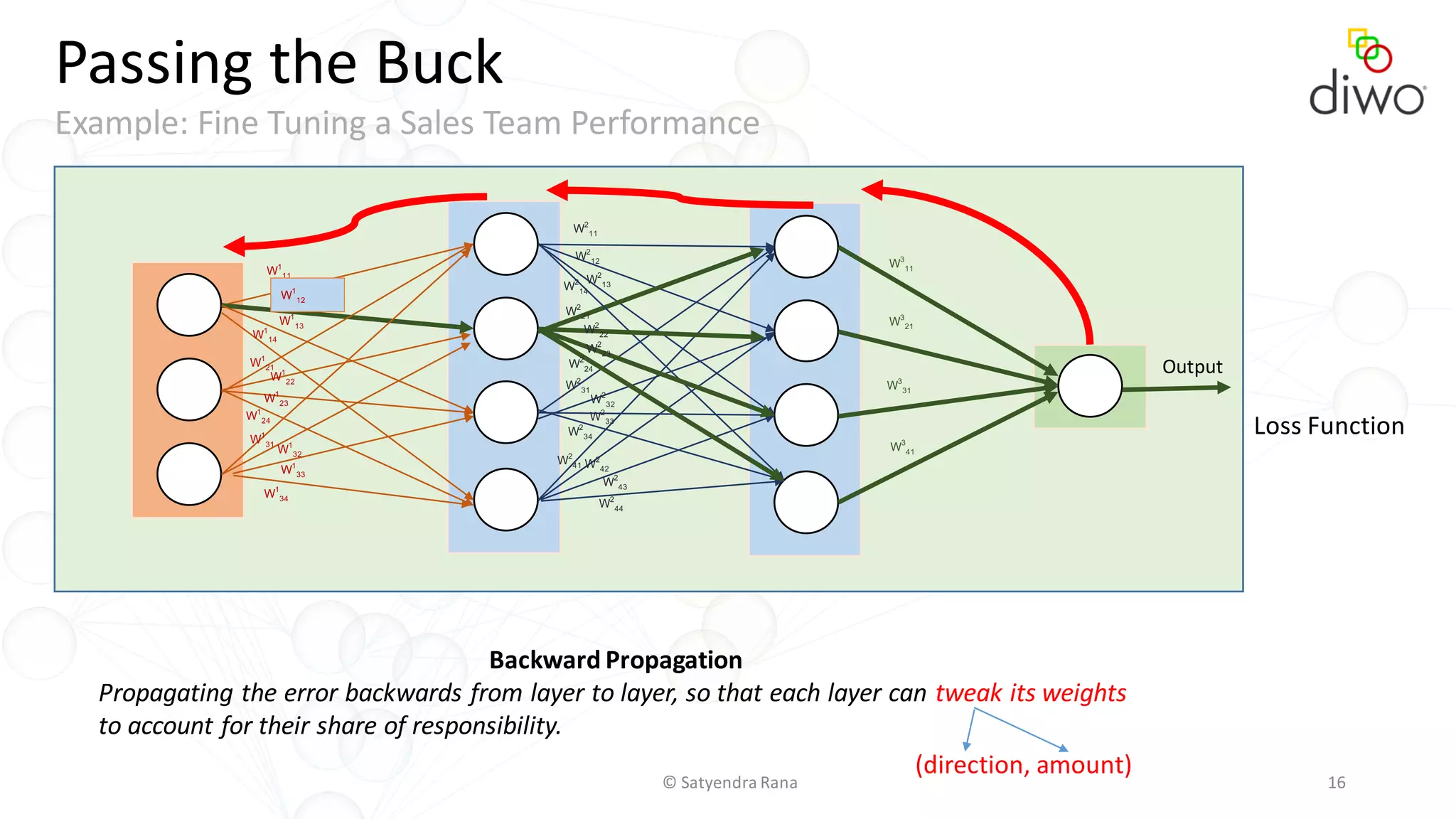
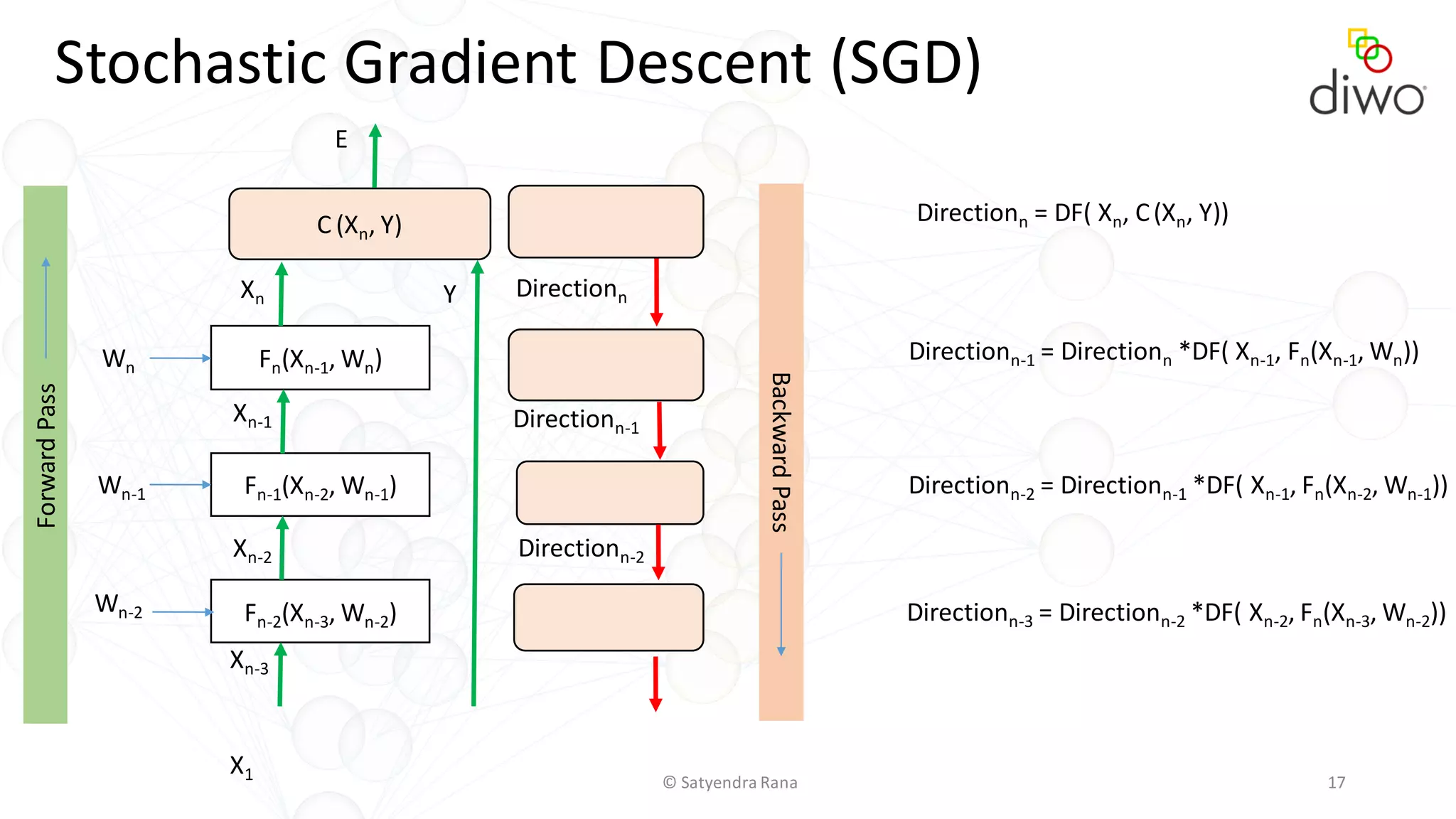
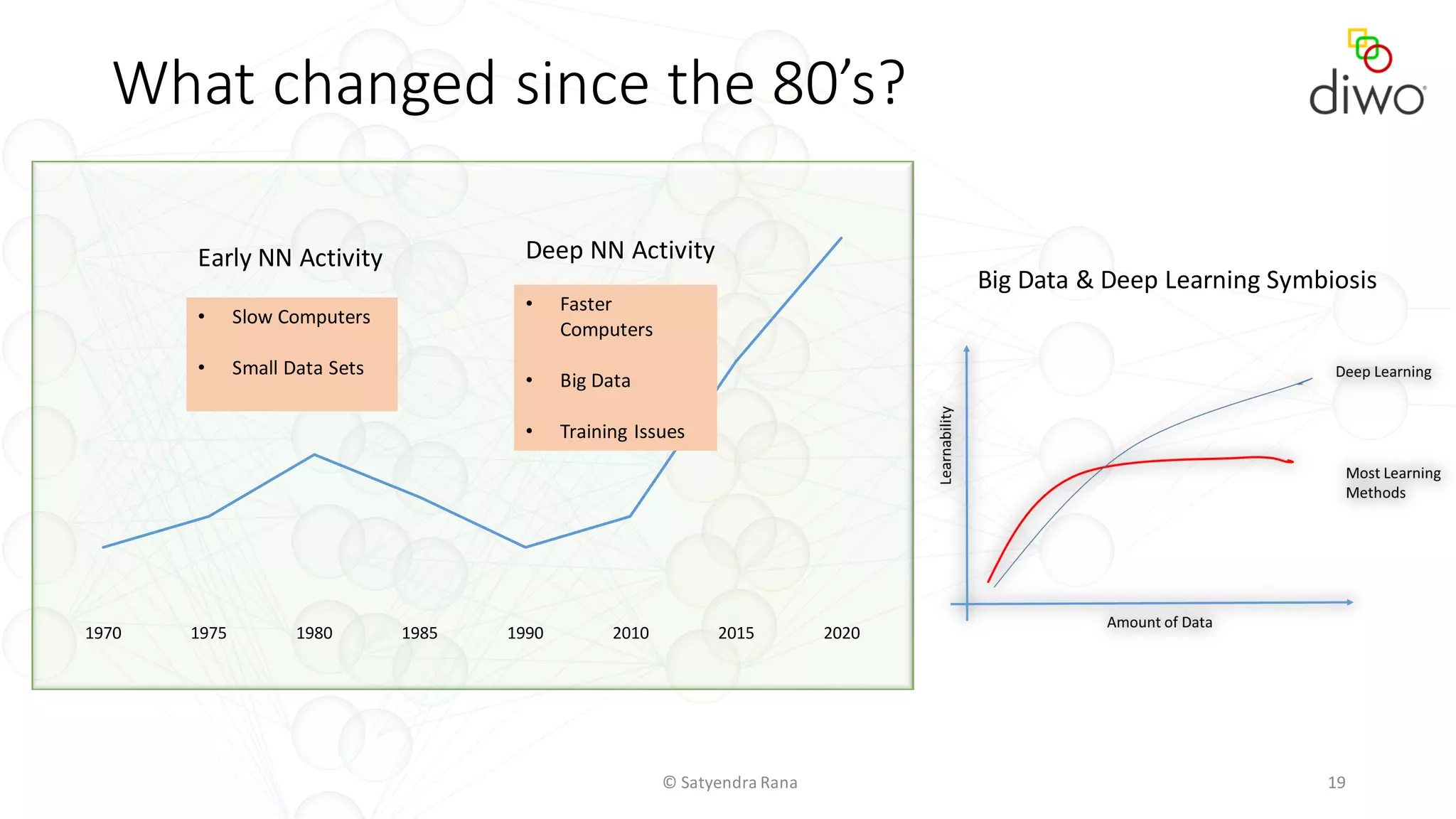
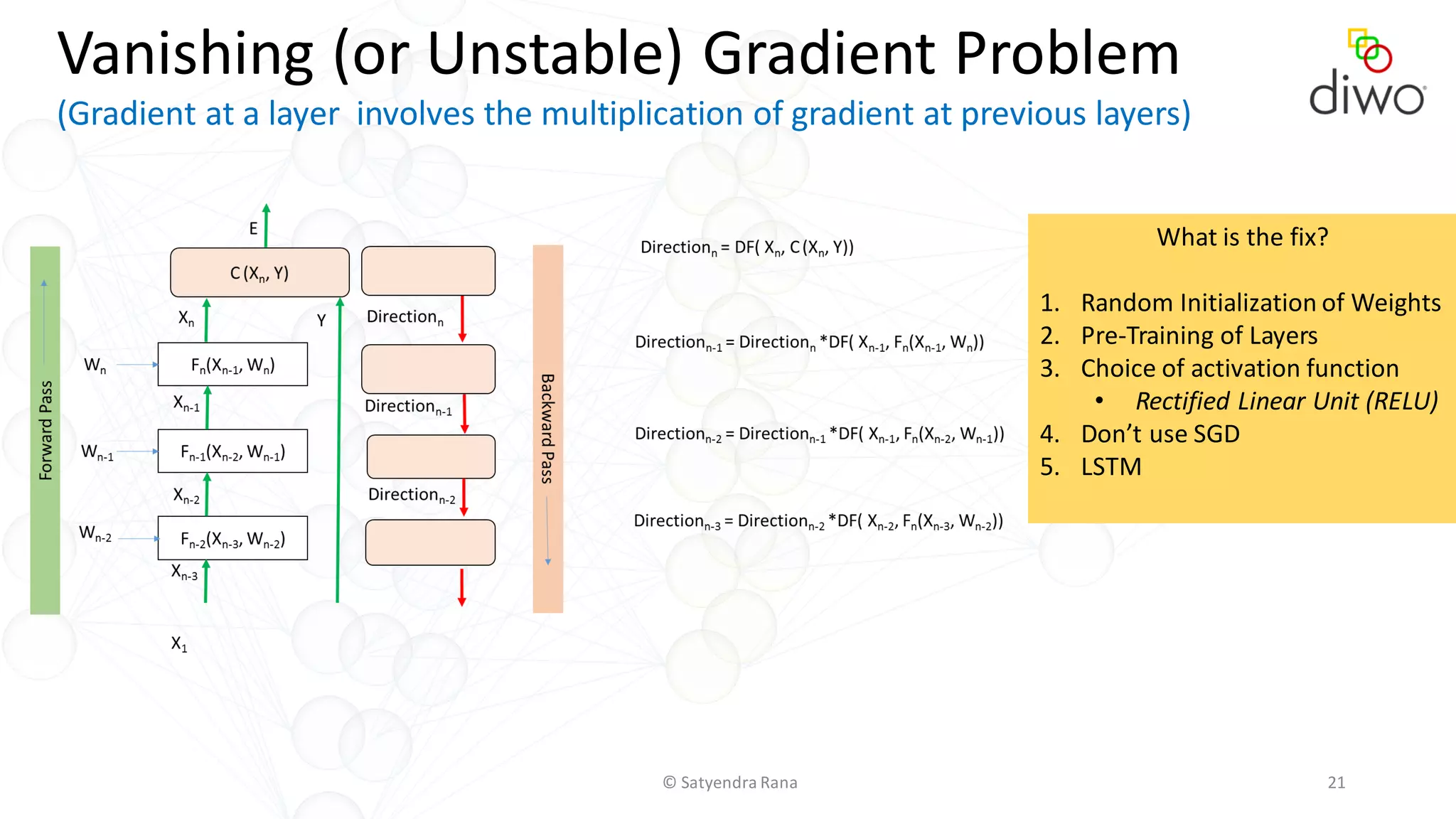
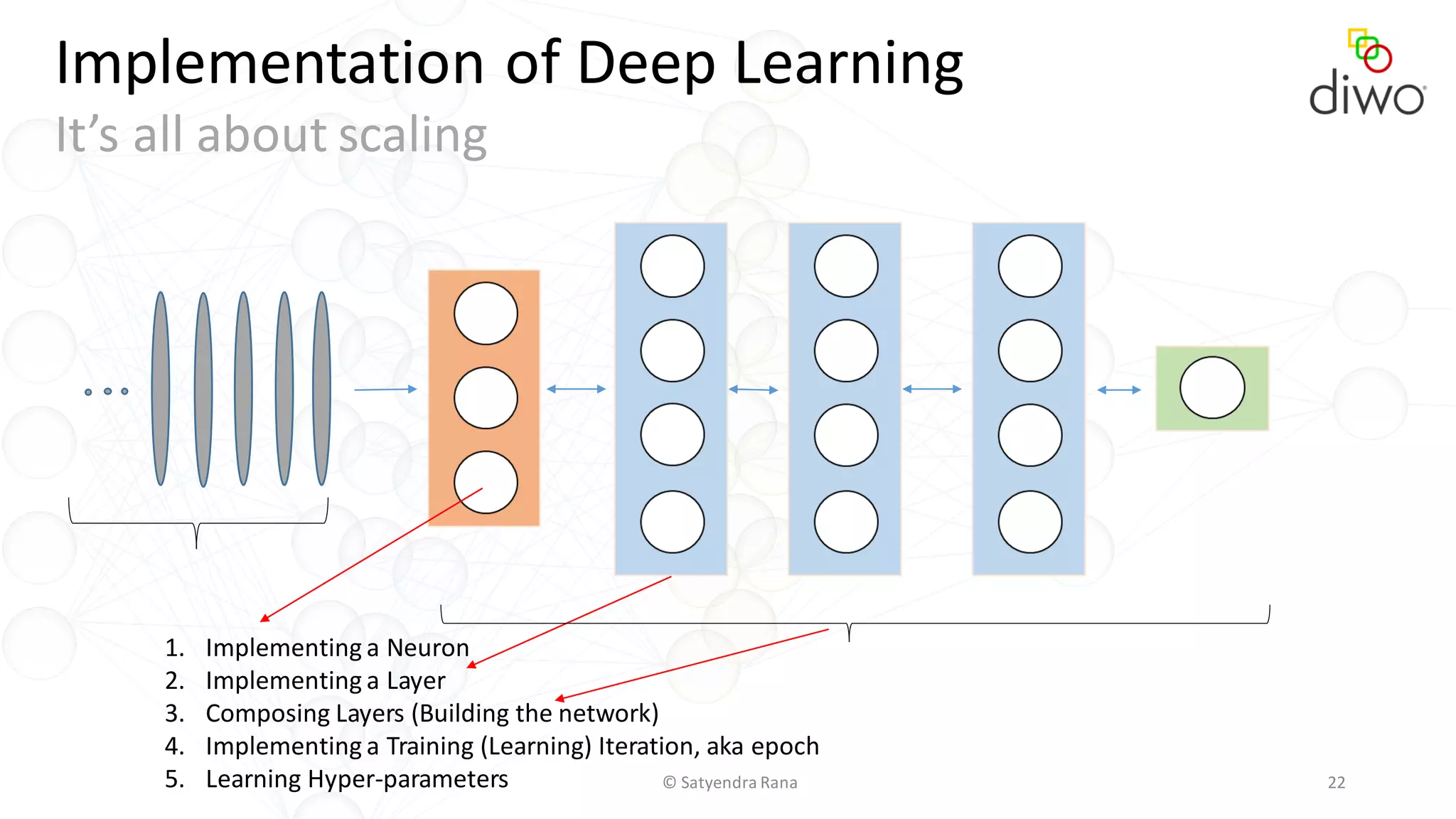
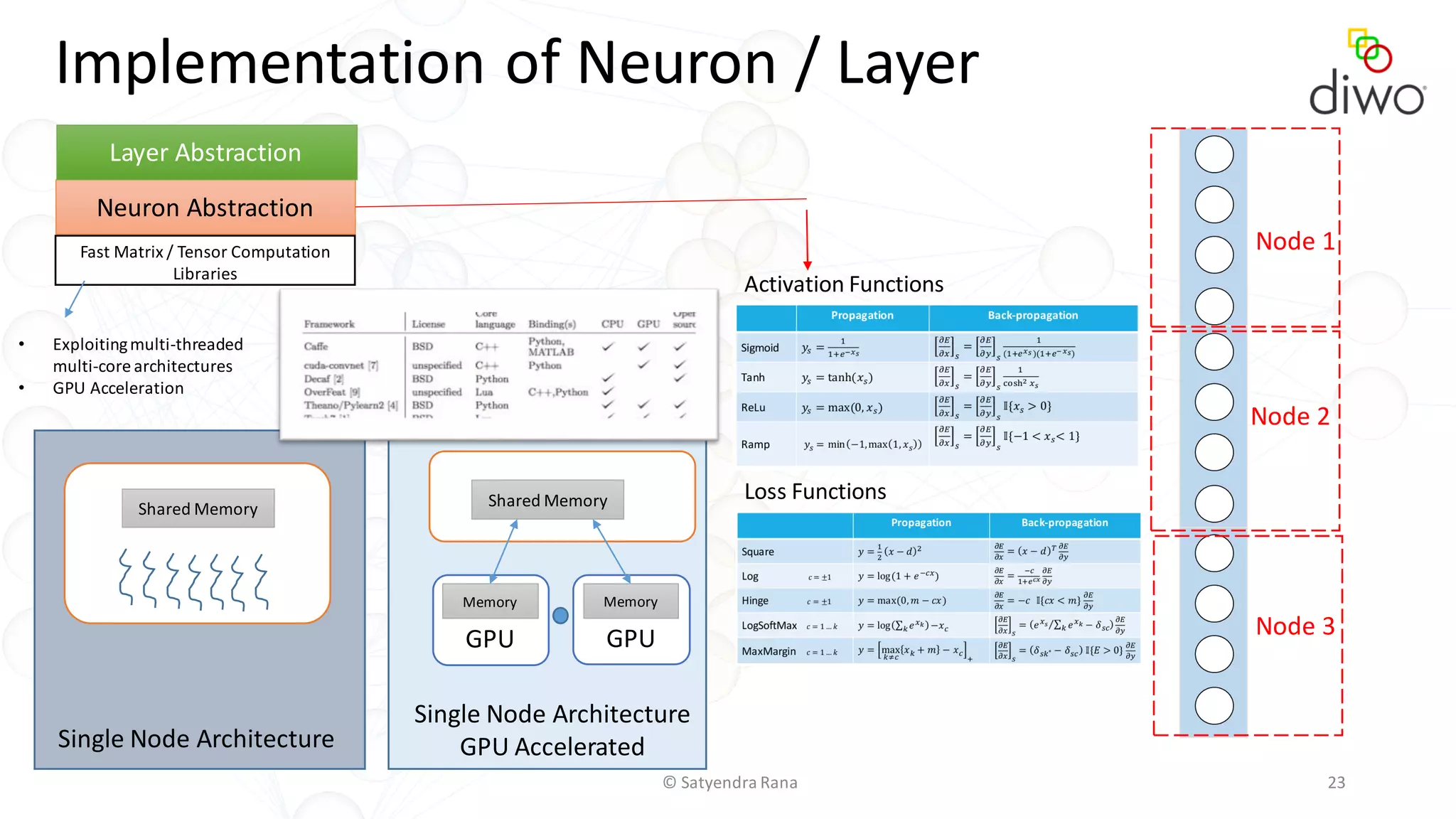
The document discusses various aspects of machine learning, particularly focusing on neural networks, their architecture, and learning methods. It highlights the importance of deep learning, types of neural networks, training techniques, and overcoming challenges such as the vanishing gradient problem. Additionally, it emphasizes the integration of deep learning with distributed computing frameworks like Apache Spark for efficient model training.

1. 1

2. Learning is about acquiring the ability
to discriminate.
Memorization
Overfitting
Under fitting
Generalization
© Satyendra Rana 2
2 2 4
2 3 5
2 4 6
2 5 7
2 3 ?
2 7 ?
3 4 ?
2 2 4.05
2 3 4.98
4 2 5.95
2 5 7.06
2 3 ?
2 7 ?
3 4 ?
Noise

3. Machine Learning
Data In Wisdom Out
© Satyendra Rana 3
?
Square Boxes
Thin
Rectangular
Boxes
Round
Boxes
Q1: Which type of box should we
look for?
Q2: Having picked up the box type,
how do we find the right box?
Computational
Architecture
Learning
Method

4. Deep (Machine) Learning
Data In Wisdom Out
© Satyendra Rana 4
?
Type of box?
Right box?
Computational
Architecture
Learning
Method
Discrimination Ability?
Finer Discrimination
(Non-linearity)
Network of Neurons
(aka Neural Network or NN)

5. © Satyendra Rana 5
Natural Language Generation

6. © Satyendra Rana 6
Machine Translation

7. © Satyendra Rana 7
Automatic Image Captioning

8. © Satyendra Rana 8
Automatic Colorization of Gray Scale Images
Input Image
Automatically
Colorized
Ground-Truth
Source:
Nvidia news

9. © Satyendra Rana 9
Ping Pong Playing Robot
Source:
Omron Automation Lab
Kyoto, Japan

10. © Satyendra Rana 10
Deep learning for the sight-impaired
(and also for the sight-endowed)

11. © Satyendra Rana 11
Neurons
Adult Brain - 100 Trillion
Infant Brain – 1 Quadrillion
Synapses

12. © Satyendra Rana 12
Model of a Neuron & Artificial Neural Networks
I
N
P
U
T
w0
w1
w2
w3
w4
Hyper-parameters
- number of layers
- type & number of neurons in each layer
Parameters
- weights (one for each connection)

13. © Satyendra Rana 13
Multi-layered Neural Network
Synapse Scale
Typical NNs - 1-10 Million
Google Brain – 1 Billion
More Recent Ones – 10 Billion
 Given a fixed number of neurons, spreading them
in more layers (deep structure) is more effective
than in fewer layers (shallow structure).
 Given a fixed number of layers, higher number of
neurons is better than fewer.
 Deep Neural Networks are powerful, but they
must also be trainable to be useful.
 Different kinds of Deep Neural Networks
 Feed Forward NNs
 Recurrent NNs
 Recursive NNs
 Convolutional NNs

14. © Satyendra Rana 14
How does a Neural Network Learn?
Parameters
Learning problem is to find the best combination of
parameter values, among all possible choices, which would
give us on an average most accurate (or minimum error)
result (output) in all possible situations (inputs).

15. © Satyendra Rana 15
Feed Forward Neural Network (FNN)
W1
11
W1
12
W1
13
W1
14
W1
21
W1
22
W1
23
W1
24
W1
31
W1
32
W1
33
W1
34
W2
11
W2
12
W2
13W2
14
W2
21
W2
22
W2
23
W2
24
W2
31
W2
32
W2
33
W2
34
W2
41 W2
42
W2
43
W2
44
W3
21
W3
11
W3
31
W3
41
Loss Function
Output
Credit Assignment Problem
Which modifiable components of a learning system are responsible for its success or failure?
How can I modify the responsible components to improve the system?
How do I change the weights (parameters) to make the NN exhibit desired behavior?
Supervised Learning

16. © Satyendra Rana 16
Passing the Buck
Example: Fine Tuning a Sales Team Performance
W1
11
W1
12
W1
13
W1
14
W1
21
W1
22
W1
23
W1
24
W1
31
W1
32
W1
33
W1
34
W2
11
W2
12
W2
13W2
14
W2
21
W2
22
W2
23
W2
24
W2
31
W2
32
W2
33
W2
34
W2
41 W2
42
W2
43
W2
44
W3
21
W3
11
W3
31
W3
41
Loss Function
Output
Backward Propagation
Propagating the error backwards from layer to layer, so that each layer can tweak its weights
to account for their share of responsibility.
(direction, amount)

17. © Satyendra Rana 17
Fn-2(Xn-3, Wn-2)
Fn-1(Xn-2, Wn-1)
Fn(Xn-1, Wn)Wn
Wn-2
Wn-1
Xn-1
Xn-2
Xn-3
X1
Xn
C (Xn, Y)
Y
E
Directionn
Directionn-1
Directionn-2
ForwardPass
BackwardPass
Directionn = DF( Xn, C(Xn, Y))
Directionn-1 = Directionn *DF( Xn-1, Fn(Xn-1, Wn))
Directionn-2 = Directionn-1 *DF( Xn-1, Fn(Xn-2, Wn-1))
Directionn-3 = Directionn-2 *DF( Xn-2, Fn(Xn-3, Wn-2))
Stochastic Gradient Descent (SGD)

18. © Satyendra Rana 18
Base camp
You are here
Climbing down Mountains with Zero Gravity
Steepest Descent
Learning rate
Epoch

19. © Satyendra Rana 19
What changed since the 80’s?
1970 1975 1980 1985 1990 2010 2015 2020
Early NN Activity Deep NN Activity
• Slow Computers
• Small Data Sets
• Faster
Computers
• Big Data
• Training Issues
Big Data & Deep Learning Symbiosis

20. © Satyendra Rana 20
Reaching Saturation Point in Learning
I don’t want to learn anymore.

21. © Satyendra Rana 21
Vanishing (or Unstable) Gradient Problem
(Gradient at a layer involves the multiplication of gradient at previous layers)
What is the fix?
1. Random Initialization of Weights
2. Pre-Training of Layers
3. Choice of activation function
• Rectified Linear Unit (RELU)
4. Don’t use SGD
5. LSTM

22. © Satyendra Rana 22
Implementation of Deep Learning
It’s all about scaling
1. Implementing a Neuron
2. Implementing a Layer
3. Composing Layers (Building the network)
4. Implementing a Training (Learning) Iteration, aka epoch
5. Learning Hyper-parameters

23. © Satyendra Rana 23
Implementation of Neuron / Layer
Neuron Abstraction
Layer Abstraction
Fast Matrix / Tensor Computation
Libraries
• Exploitingmulti-threaded
multi-core architectures
• GPU Acceleration
Single Node Architecture
Shared Memory Shared Memory
Memory
GPU
Memory
GPU
Single Node Architecture
GPU Accelerated
Activation Functions
Loss Functions
Node 1
Node 2
Node 3

24. © Satyendra Rana 24
Composing Layers / Building a Neural Network
1. Specifying Layer Composition
(network specification)
SparkML
val mlp = new MultilayerPerceptronClassifier()
.setLayers(Array(784, 300, 100, 10))
.setBlockSize(128)
SparkNet
val netparams = NetParams(
RDDLayer(“data”, shape=List(batchsize, 1, 28, 28)),
RDDLayer(“label”, shape=List(batchsize, 1)),
ConvLayer(“conv1”, List(“data”), Kernel=(5,5), numFilters=20),
PoolLayer(“pool1”, List(“conv1”), pool=Max, kernel=(2,2), stride=(2,2)),
ConvLayer(“conv2”, List(“pool1”), Kernel=(5,5), numFilters=50),
PoolLayer(“pool2”, List(“conv2”), pool=Max, kernel=(2,2), stride=(2,2)),
LinearLayer(“ip1”, List(“pool2”), numOutputs=500),
ActivationLayer(“relu1”, List(“ip1”), activation=ReLU),
LinearLayer(“ip2”, List(“relu1”), numOutputs=10),
SoftmaxWithLoss(“loss”, List(“ip2”, “label”))
)
2. Allocating layers to nodes

25. © Satyendra Rana 25
Speeding up the Training Iteration
Distributed Implementation of SGD
Executor 1
BLAS
Master
Executor n
BLAS
Wk
Wk
Step 1: Get parameters from Master
Step 2: Compute gradient
Step 3: Send gradients to Master
Master
Step 4: Compute Wk+1 from gradients
Wk+1
Wk+1
Iteration k
BLAS: Basic Linear Algebra Subprograms, use in Spark thru NetLib-java

26. © Satyendra Rana 26
MultilayerPerceptronClassifier() in Spark ML
Scala Code
val digits: DataFrame = sqlContext.read.format(“libsvm”).load(“/data/mnist”)
val mlp = new MultilayerPerceptronClassifier()
.setLayers(Array(784, 300, 100, 10))
.setBlockSize(128)
val model=mlp.fit(digits)
Features
(input)
Classes (output)
Hidden layer
With 300
neurons
Hidden layer
With 100
neurons

27. © Satyendra Rana 27
SparkNet: Training Deep Networks in Spark
Executor 3
GPU Caffe
Executor 2
GPU Caffe
Executor 1
GPU Caffe
Executor 4
GPU Caffe
Master
Data Shard 1
Data Shard 2 Data Shard 3
Data Shard 4
2. Run SGD on a mini-batch
for a fixed time/iterations
3. Send parameters to master
1. Broadcast model parameters
4. Receive parameters from executors
5. Average them to get new parameters
2. Run SGD on a mini-batch
for a fixed time/iterations
3. Send parameters to master
2. Run SGD on a mini-batch
for a fixed time/iterations
3. Send parameters to master
2. Run SGD on a mini-batch
for a fixed time/iterations
3. Send parameters to master

28. © Satyendra Rana 28
with
Best Model
Model # 1
Training
Model # 2
Training
Model # 3
Training
Distributed Cross Validation

29. © Satyendra Rana 29
Apache SINGA
A General Distributed Deep Learning Platform

30. Why “Deep Learning” on Spark?
 Sorry, I don’t have a GPU / GPU Cluster
 A 3-to-5 node Spark cluster can be as fast as a GPU
 Most of my application and data resides on a Spark Cluster
Integrating Model Training with existing data-processing pipelines
High-throughput loading and pre-processing of data and the ability to keep
data in between operations.
Hyper-parameter learning
Poor man’s deep learning
 It’s simply fun …
© Satyendra Rana 30