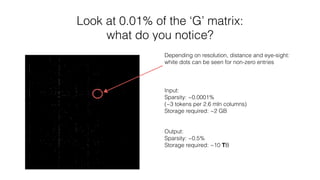
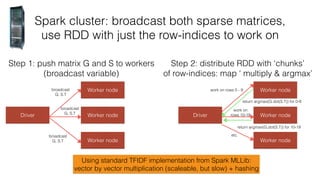
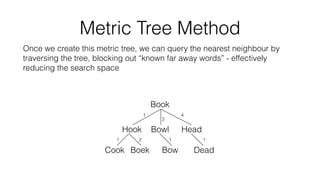
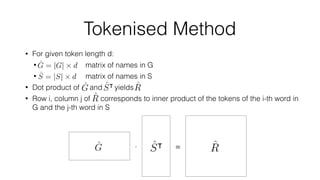
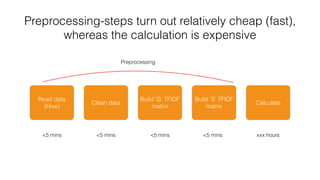
The document discusses the challenges of matching company names in large datasets due to variations in naming conventions, presenting three main approaches to solve the problem: brute force, metric tree, and tokenised methods. It highlights the inefficiencies of brute force due to high computational demands and introduces the tokenised method as a more efficient alternative by using matrix calculations and cosine similarity. The current status indicates ongoing optimization efforts using different computational resources like GPUs and Spark clusters for faster processing.

1. Name Matching at Scale:
CPU, GPU or SPARK?
Wendell Kuling and Chris Broeren
ING Wholesale Banking Advanced Analytics Team

2. Chris Broeren,
Data Scientist
Wendell Kuling,
Data Scientist

3. Overview
• Introduction to problem
• Methods to solve problem
• Brute Force approach
• Metric tree approach
• Tokenised approach
• Current status

4. Introduction
Wholesale bank = dealing with companies
Interested in different data sets about companies
To join multiple data sets together, we need a common key: company name
However one company may be called by different name:
: McDonalds Corporation, McDonalds, McDonald’s Corp, etc…
Therefore we need to match approximately similar names of companies
together

5. Introduction
Define an existing list of company names as the ground truth (G)
Aim: match new sets of names (S1, S2, S3, … ) with G:
Without loss of generality, let’s assume we’re going to match one set of names, S with G for this talk
ABN Amro Bank
RBS Bank
Rabobank
JP Morgan
ING Groep
ASN Bank
Chase Bank
BINCK Bank
HSBC Bank
Westpac Bank
Goldman Sachs
ABN Amro N.V
RBS LLC
Rabobank NV
JPM USA
ING Groep N.V.
ASN
Chase
BINCK N.V
HSBC
Westpac Australia
GS Global
Source 1Ground Truth
ABN Amro N.V
RBS LLC
Rabobank N.V
JPM USA
ING Groep
ASN
Chase
BINCK N.V
HSBC
Westpac
GS Global
Source 2
ABN Amro N.V
RBS LLC
RABOBANK NV
JPM USA
ING N.V.
ASN
Chase Bank
BINCK N.V
HSBC
Westpac Aus
GS Global
Source 3
G S1 S2 S3

6. Introduction
Many ways to look at problem:
• Approximate string match problem
• Nearest Neighbour Search problem
• Pattern matching
• etc…
We need to find the “closest” name in G to match to every name in S

7. Reality
In our first case:
• G has 12 million names
• S ranges in length between 3000 and 5 mln names
To make matters worse:
• On average, a name is 31 characters long, containing ~4 words
• The world isn’t UTF8 compliant, we have over 160 characters
• Although there are limited duplicates in G, some companies have similar
names and have hierarchical structures which must be observed

8. Overview
• Introduction to problem
• Methods to solve problem
• Brute Force approach
• Metric tree approach
• Tokenised approach
• Current status

9. Brute Force Method
Define a function to measure word closeness:
The closer the names are to each other, the more similar they are
Calculate closeness for each word and choose the closest
Ensemble with different functions to get better results

10. Brute Force Method
There are many word similarity functions. An example is the Levenshtein distance.
Levenshtein distance calculates the minimum number of character edits
(replacing, adding or subtracting) it takes to make two strings equal.
Example: levenshtein(“ABN Amro Bank”, “RBS Bank”)
• ABN Amro Bank —> RBN Amro Bank (replace A with R)
• RBN Amro Bank —> RBN Bank (remove Amro)
• RBN Bank —> RBS Bank (replace N with S)
Therefore Levenshtein(“ABN Amro Bank”, “RBS Bank”) = 1 + 4 + 1

11. Brute Force Method
• “ABN Amro Bank” vs {“ABN Amro N.V, … , “GS Global”}
ABN Amro Bank
RBS Bank
Rabobank
JP Morgan
ING Groep
ASN Bank
Chase Bank
BINCK Bank
HSBC Bank
Westpac Bank
Goldman Sachs
ABN Amro N.V
RBS LLC
Rabobank NV
JPM USA
ING Groep N.V.
ASN
Chase
BINCK N.V
HSBC
Westpac Australia
GS Global
SG

12. Brute Force Method
• “RBS Bank” vs {“ABN Amro N.V, … , “GS Global”}
ABN Amro Bank
RBS Bank
Rabobank
JP Morgan
ING Groep
ASN Bank
Chase Bank
BINCK Bank
HSBC Bank
Westpac Bank
Goldman Sachs
ABN Amro N.V
RBS LLC
Rabobank NV
JPM USA
ING Groep N.V.
ASN
Chase
BINCK N.V
HSBC
Westpac Australia
GS Global
SG

13. Brute Force Method
• “Goldman Sachs” vs {“ABN Amro N.V, … , “GS Global”}
ABN Amro Bank
RBS Bank
Rabobank
JP Morgan
ING Groep
ASN Bank
Chase Bank
BINCK Bank
HSBC Bank
Westpac Bank
Goldman Sachs
ABN Amro N.V
RBS LLC
Rabobank NV
JPM USA
ING Groep N.V.
ASN
Chase
BINCK N.V
HSBC
Westpac Australia
GS Global
SG

14. Brute force method
• Problem: 12 million names in G, 5 million names in S
• This is 60,000,000,000,000 similarity calculations
• Levenshtein algorithm has time complexity of O(mn), where m, n are length
of strings.
• If we could calculate 10 similarity calculations a second…We would be
here for ~ 190,000 years
• Parallel: 10,000 cores … 19 years

15. Know which package to use for edit-based
distances

16. Fuzzywuzzy: string matching like a boss… but for
smaller sets only

17. Overview
• Introduction to problem
• Methods to solve problem
• Brute Force approach
• Metric tree approach
• Tokenised approach
• Current status

18. Metric Tree Method
We can think of names as points in some topological space
We don’t necessarily need to know absolute location of a word in a space, just the
relative distance between points
Therefore we still use a distance function (as per brute force), but define it so it
satisfies some mathematical properties:
1. d(x,y) = 0 —> x = y
2. d(x,y) = d(y,x)
3. d(x,z) <= d(x,y) + d(y,z)
This is known as a is a metric, we can save ourself time by organising the words into a
tree structure that preserves metric-distances between words

19. Metric Tree Method
Once we create this metric tree, we can query the nearest neighbour by
traversing the tree, blocking out “known far away words” - effectively
reducing the search space
Book
BowlHook Head
Cook Boek Bow Dead
1
2
4
1 2 1 1

20. Metric Tree Method
Building the tree, is well feasible with ~2.7 mln different words - O(n log(n))
Typically, all words with distance of 1 determined in ~1 sec
Build + query time still years worth of calculation
• Added problem of making a tree in parallel
• Lots of space required
• Worst case performance is actually bad

21. Overview
• Introduction to problem
• Methods to solve problem
• Brute Force approach
• Metric tree approach
• Tokenised approach
• Current status

22. Tokenised Method
Break name up into components (tokenising)
Many different types of tokens available: words, grams
Do this for all names in both G and S (this creates two matrices [names x tokens])
Example: Indicator function word tokeniser:
ABN RBS BANK Rabobank NV
ABN Amro
Bank
1 0 1 0 0
RBS Bank 0 1 1 0 0
Rabobank NV 0 0 0 1 1

23. Tokenised Method
• For given token length d:
• matrix of names in G
• matrix of names in S
• Dot product of and yields
• Row i, column j of corresponds to inner product of the tokens of the i-th word in
G and the j-th word in S
=.

24. Tokenised Method
• Why the dot product?
• The elements of look somewhat familiar to us:
• elements are the cosine similarity of the individual name-token vectors
multiplied by the L2 norm
• If we normalise the token-vector on creation we end up calculating the
cosine-similarity measure!

25. Tokenised Method
• Same number of total comparisons as brute-force
• But inner-products are cheap to calculate
• Tokenised matrices can be computed offline cheaply
• Tokenised methods allow for vectorisation and allow for increased memory
and CPU efficiency
• We can even compute this on a GPU cluster

26. Overview
• Introduction to problem
• Methods to solve problem
• Brute Force approach
• Metric tree approach
• Tokenised approach
• Current status

27. Preprocessing-steps turn out relatively cheap (fast),
whereas the calculation is expensive
Read data
(Hive)
Clean data
Build ‘G’ TFIDF
matrix
Build ‘S’ TFIDF
matrix
<5 mins <5 mins <5 mins xxx hours
Preprocessing
Calculate
<5 mins

28. Things you would wish you knew before (1/4)…
Read data
(Hive)
Runs out of memory

29. (or use Python 3.x ;))
Clean data
Things you would wish you knew before (2/4)…
tokenize(‘McDonaldś’)

30. Build ‘G’ TFIDF
matrix
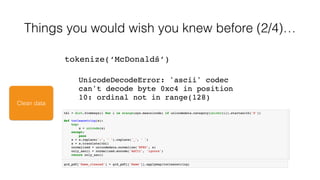
Things you would wish you knew before (3/4)…
Standard token_pattern (‘(?u)bww+b’) ignores single letters
Use token_pattern (‘(?u)bw+b’) for ‘full’ tokenization
(token_pattern = u’(?u)S', ngram_range=(3, 3)) gives 3-gram matching
‘Taxibedrijf M. van Seben’ —> [‘Taxibedrijf’, ‘van’, ‘ Seben’ ]

31. Build ‘S’ TFIDF
matrix
Things you would wish you knew before (4/4)
Standard ‘transform’ function of Sklearn TFIDFVectorizer ignores unseen tokens
—> either transform using customized function, or tokenise on combination of G and S
match(‘JonasTheMan Nederland’) —> 100% match ‘Nederland Nederland’ ?

32. Calculation of cosine similarity:
matrix multiplication using Numpy/Scipy
Using Numpy and Scipy, fast Matrix multiplication of Sparse matrices. Suggested format: CSR.
.7
0
0
0
.7
1 0 0 0 0
0 .7 0 0 .7
0 0 .6 .6 .6
x
# tokens
# company
names
# of tokens (Transposed)
G S.Transpose
=
.7
.49
.42
Argmax = best match
Calculate

33. Look at 0.01% of the ‘G’ matrix:
what do you notice?
Input:
Sparsity: ~0.0001%
(~3 tokens per 2.6 mln columns)
Storage required: ~2 GB
Output:
Sparsity: ~0.5%
Storage required: ~10 TB
Depending on resolution, distance and eye-sight:
white dots can be seen for non-zero entries

34. Cruncher:
48 Cores, 512 GB RAM
Tesla:
GPUs: 3x2496 threads, 3x12 GB
Spark cluster:
150 cores, 2.5TB of memory
34
Introducing the three contestants for the
calculation part…

35. Numpy matrix multiplication:
first ~100 extra slices are cheap

36. Scipy/Numpy sparse matrix multiplication:
most expensive and highly-optimized function
Effectively using 1 core, 100 rows / iteration: ~140 matches per second
(additional memory usage: ~1 GB)

37. Tesla - GPU multiplication:
PyCuda is flexible, but requires deep C++ knowledge
Current custom kernel works with
Sparse Matrix x Dense Vector
(slice = 1)
Didn’t distribute the data across the GPU up-front
Using single GPU at the moment
…so, in short, further optimizations are possible!
Using 1 GPU, slice of 1 and Sparse x Dense multiplication:
~50 matches per second

38. Spark cluster: broadcast both sparse matrices,
use RDD with just the row-indices to work on
Driver
Step 1: push matrix G and S to workers
(broadcast variable)
Worker node
Worker node
Worker node
Step 2: distribute RDD with ‘chunks’
of row-indices: map ‘ multiply & argmax’
broadcast
G, S.T
broadcast
G, S.T
broadcast
G, S.T
Driver
Worker node
Worker node
Worker node
work on rows 0 - 9
return argmax(G.dot(S.T)) for 0-9
work on
rows 10-19
return argmax(G.dot(S.T)) for 10-19
etc.
Using standard TFIDF implementation from Spark MLLib:
vector by vector multiplication (scaleable, but slow) + hashing

39. Spark cluster: scales with only small modifications
to original Python code
612,630 matches in 12 containers, 12 cores/container, chunks
of 20 rows in ~5 min: 2000 matches / sec

40. Concluding for name-matching using Python