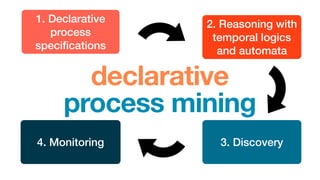
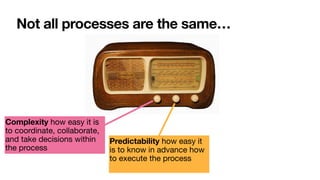
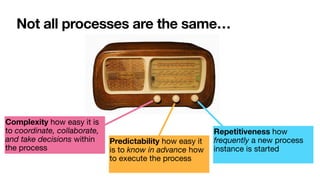
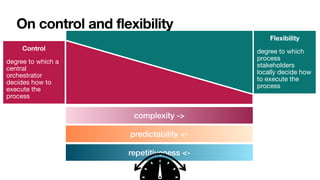
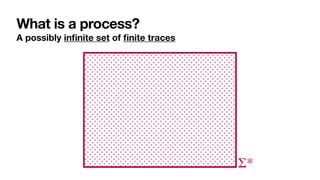
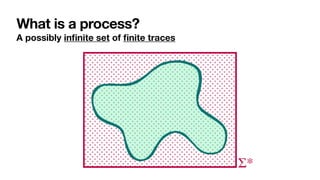
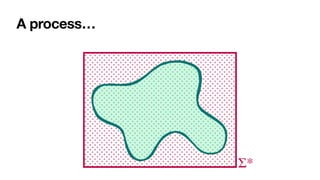
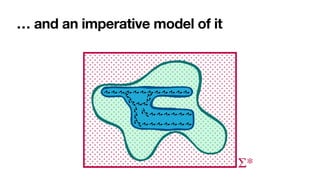
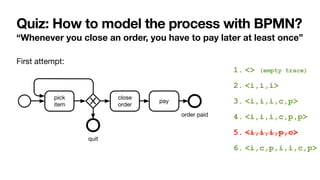
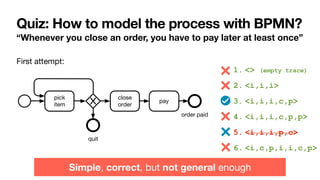
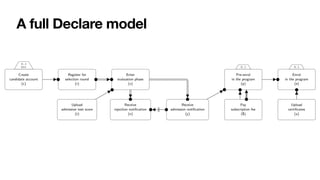
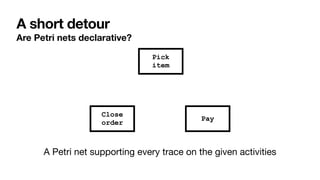
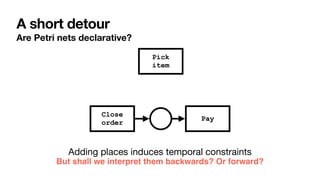
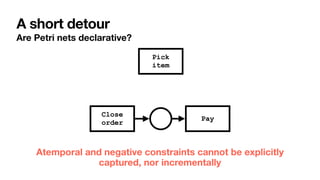
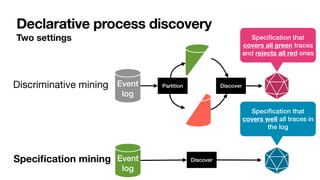
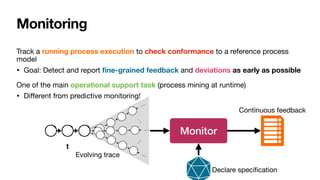
The document discusses declarative process mining, outlining the principles of declarative process specifications, discovery, monitoring, and reasoning with temporal logics. It highlights the complexity, predictability, and flexibility of processes, and contrasts imperative and declarative modeling paradigms. Moreover, it elaborates on the significance of constraints, templates, and their applications in business process management, particularly using languages like Declare and linear temporal logic.

























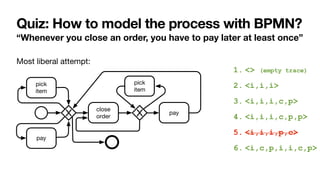
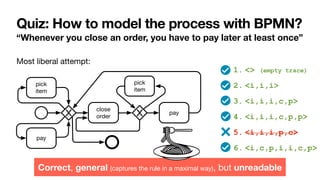



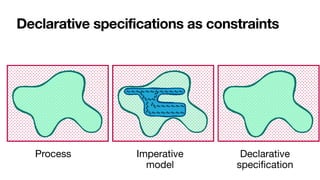
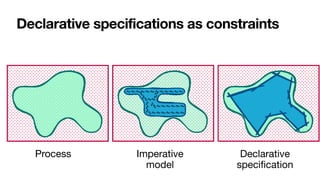
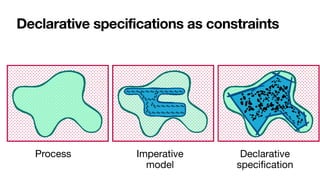
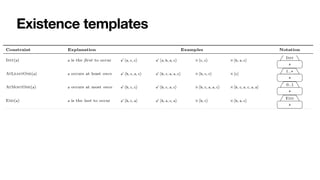
![Constraint-based specifications of behaviour
• Multiagent systems: declarative agent programs [Fisher,JSC1996]
and interaction protocols [Singh,AAMAS2003]
• Data management: cascaded transactional updates
[DavulcuEtAl,PODS1998]
• BPM (1st wave): loosely-coupled subprocesses [SadiqEtAl,ER2001]
• BPM (2nd wave): process constraints
• DECLARE [PesicEtAl,EDOC2007]
• Dynamic Condition-Response (DCR) Graphs
[HildebrandtEtAl,PLACES2010]](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-53-320.jpg)






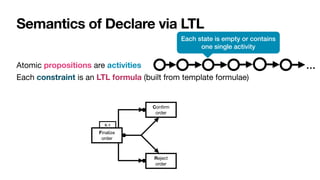
![Interaction among constraints
Aka hidden dependencies [MontaliEtAl,TWEB2010]
Cancel
order
Confirm
order
Pay
If you cancel the order, you
cannot pay for it
If you con
fi
rm the order,
you must pay for it](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-65-320.jpg)
![Interaction among constraints
Aka hidden dependencies [MontaliEtAl,TWEB2010]
Cancel
order
Confirm
order
Pay
If you cancel the order, you
cannot pay for it
If you con
fi
rm the order,
you must pay for it
Hence:
forbidden to
cancel and
con
fi
rm!
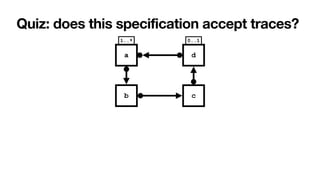
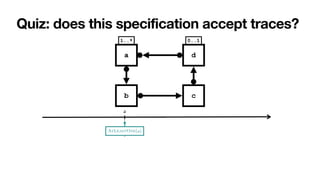
Key questions
1. How to
characterise the
language of a
Declare
speci
fi
cation?
2. How to
understand
whether a
speci
fi
cation is
correct?](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-66-320.jpg)



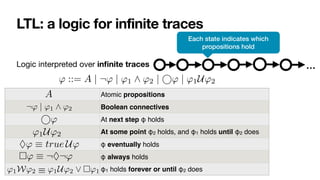
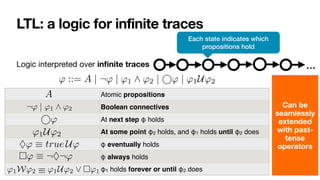
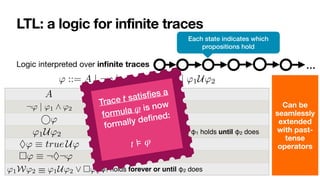

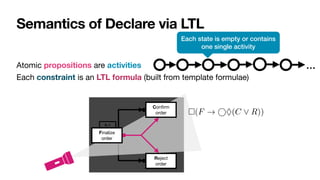
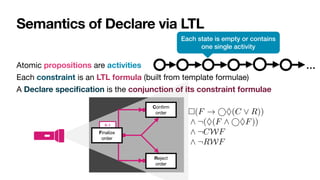



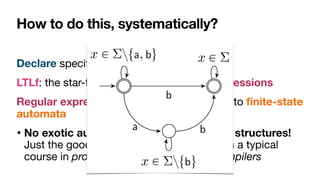
![LTLf: LTL over finite traces
[DeGiacomoVardi,IJCAI2013]
LTL interpreted over
fi
nite traces
' ::= A | ¬' | '1 ^ '2 | ' | '1U'2
No successor!
Same syntax of LTL
In LTL, there is always a next moment… in LTLf, the contrary!
φ always holds from current to the last instant
The next step exists and at next step φ holds
(weak next) If the next step exists, then at next step φ holds
last instant in the trace
' | '1 ^ '2 | ' | '1U'2
⇤'
Last ⌘ ¬ true
' ⌘ ¬ ¬'](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-84-320.jpg)
![Look the same, but they are not the same
Many researchers: misled by moving from in
fi
nite to
fi
nite traces
In [DeGiacomoEtAl,AAAI14], we studied why!
• People typically focus on “patterns”, not on the entire logic
• Many of such patterns in BPM, reasoning about actions, planning, etc. are
“insensitive to in
fi
nity”](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-85-320.jpg)
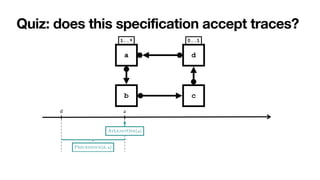
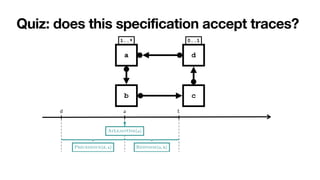
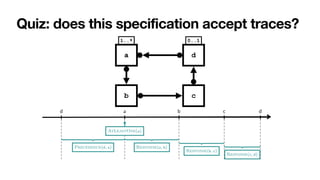
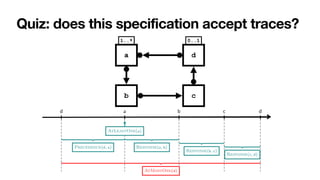

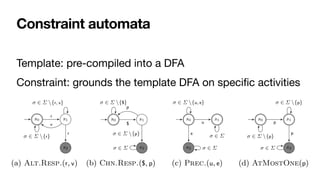
![From Declare to automata
LTLf NFA
nondeterministic
DFA
deterministic
LTLf2aut determin.
'
nt
lf formulas can be translated into equivalent nfa:
t |= Ï iff t œ L(AÏ)
/ldlf to nfa (exponential)
to dfa (exponential)
often nfa/dfa corresponding to ltlf /ldlf are in fact small!
ompile reasoning into automata based procedures!
Process engine!
[DeGiacomoVardi,IJCAI2013]
[DeGiacomoEtAl,TOSEM2022]](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-96-320.jpg)
![Vision realised!
LTLf NFA
nondeterministic
DFA
deterministic
LTLf2aut determin.
'
nt
lf formulas can be translated into equivalent nfa:
t |= Ï iff t œ L(AÏ)
/ldlf to nfa (exponential)
to dfa (exponential)
often nfa/dfa corresponding to ltlf /ldlf are in fact small!
ompile reasoning into automata based procedures!
Process engine!
[DeGiacomoVardi,IJCAI2013]
[DeGiacomoEtAl,TOSEM2022]](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-97-320.jpg)
![Few lines of code
[DeGiacomoEtAl,TOSEM2022]
0:8 G. De Giacomo et al.
(tt, ⇧) = true
(↵ , ⇧) = false
( , ⇧) = (h itt, ⇧) ( prop.)
('1 ^ '2, ⇧) = ('1, ⇧) ^ ('2, ⇧)
('1 _ '2, ⇧) = ('1, ⇧) _ ('2, ⇧)
(h i', ⇧) =
⇢
E (') if ⇧ |= ( prop.)
false if ⇧ 6|=
(h ?i', ⇧) = ( , ⇧) ^ (', ⇧)
(h⇢1 + ⇢2i', ⇧) = (h⇢1i', ⇧) _ (h⇢2i', ⇧)
(h⇢1; ⇢2i', ⇧) = (h⇢1ih⇢2i', ⇧)
(h⇢⇤
i', ⇧) = (', ⇧) _ (h⇢iF h⇢⇤i', ⇧)
([ ]', ⇧) =
⇢
E (') if ⇧ |= ( prop.)
true if ⇧ 6|=
([ ?]', ⇧) = (nnf (¬ ), ⇧) _ (', ⇧)
([⇢1 + ⇢2]', ⇧) = ([⇢1]', ⇧) ^ ([⇢2]', ⇧)
([⇢1; ⇢2]', ⇧) = ([⇢1][⇢2]', ⇧)
([⇢⇤
]', ⇧) = (', ⇧) ^ ([⇢]T [⇢⇤]', ⇧)
(F , ⇧) = false
(T , ⇧) = true
Fig. 1: Definition of , where E (') recursively replaces in ' all occurrences of atoms of
the form T and F by .
1: algorithm LDLf 2NFA
2: input LDLf formula '
3: output NFA A(') = (2P
, S, s0, %, Sf )
4: s0 {'} . set the initial state
5: Sf {;} . set final states
6: if ( (', ✏) = true) then . check if initial state is also final
7: Sf Sf [ {s0}
8: S {s0, ;}, % ;
9: while (S or % change) do
10: for (s 2 S) do
11: if (s0
|=
V
( 2s) ( , ⇧) then . add new state and transition
12: S S [ {s0
}
13: % % [ {(s, ⇧, s0
)}
14: if (
V
( 2s0) ( , ✏) = true) then . check if new state is also final
15: Sf Sf [ {s0
}
Fig. 2: NFA construction.
' NFA](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-98-320.jpg)
![Few lines of code
[DeGiacomoEtAl,TOSEM2022]
0:8 G. De Giacomo et al.
(tt, ⇧) = true
(↵ , ⇧) = false
( , ⇧) = (h itt, ⇧) ( prop.)
('1 ^ '2, ⇧) = ('1, ⇧) ^ ('2, ⇧)
('1 _ '2, ⇧) = ('1, ⇧) _ ('2, ⇧)
(h i', ⇧) =
⇢
E (') if ⇧ |= ( prop.)
false if ⇧ 6|=
(h ?i', ⇧) = ( , ⇧) ^ (', ⇧)
(h⇢1 + ⇢2i', ⇧) = (h⇢1i', ⇧) _ (h⇢2i', ⇧)
(h⇢1; ⇢2i', ⇧) = (h⇢1ih⇢2i', ⇧)
(h⇢⇤
i', ⇧) = (', ⇧) _ (h⇢iF h⇢⇤i', ⇧)
([ ]', ⇧) =
⇢
E (') if ⇧ |= ( prop.)
true if ⇧ 6|=
([ ?]', ⇧) = (nnf (¬ ), ⇧) _ (', ⇧)
([⇢1 + ⇢2]', ⇧) = ([⇢1]', ⇧) ^ ([⇢2]', ⇧)
([⇢1; ⇢2]', ⇧) = ([⇢1][⇢2]', ⇧)
([⇢⇤
]', ⇧) = (', ⇧) ^ ([⇢]T [⇢⇤]', ⇧)
(F , ⇧) = false
(T , ⇧) = true
Fig. 1: Definition of , where E (') recursively replaces in ' all occurrences of atoms of
the form T and F by .
1: algorithm LDLf 2NFA
2: input LDLf formula '
3: output NFA A(') = (2P
, S, s0, %, Sf )
4: s0 {'} . set the initial state
5: Sf {;} . set final states
6: if ( (', ✏) = true) then . check if initial state is also final
7: Sf Sf [ {s0}
8: S {s0, ;}, % ;
9: while (S or % change) do
10: for (s 2 S) do
11: if (s0
|=
V
( 2s) ( , ⇧) then . add new state and transition
12: S S [ {s0
}
13: % % [ {(s, ⇧, s0
)}
14: if (
V
( 2s0) ( , ✏) = true) then . check if new state is also final
15: Sf Sf [ {s0
}
Fig. 2: NFA construction.
' NFA
Automata manipulations
much easier to handle
than in the in
fi
nite case,
with huge performance
improvements
[ZhuEtAl,
IJ
CAI17]
[Westergaard,BPM11]](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-99-320.jpg)





















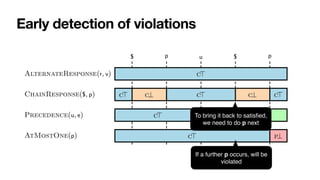
![RV-LTL truth values
[BauerEtAl,TOSEM2011]
C is permanently satis
fi
ed if t
satis
fi
es C and no matter how t is
extended, C will stay satis
fi
ed
C is currently satis
fi
ed if t satis
fi
es C
but there is a continuation of t that
violates C
…
…
t
…
…
…
t](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-139-320.jpg)
![RV-LTL truth values
C is currently violated if t violates C
but there is a continuation that leads
to satisfy C
C is permanently violated if t violates
C and no matter how t is extended, C
will stay violated
t
…
…
…
…
…
[BauerEtAl,TOSEM2011]](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-140-320.jpg)
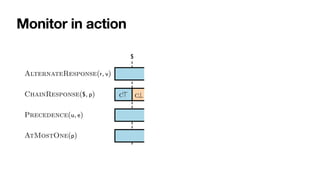
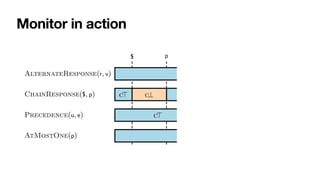
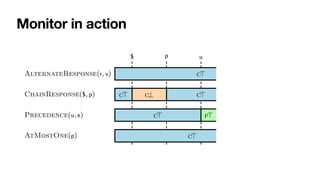
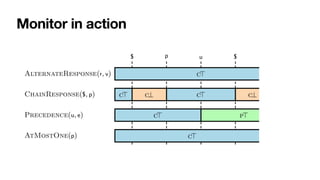
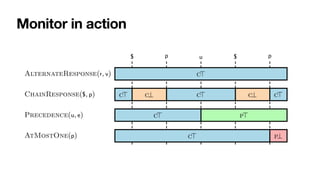
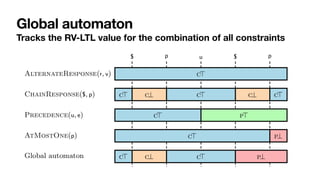
![Monitoring by coloring automata
[MaggiEtAl,BPM2011] [DeGiacomoEtAl,TOSEM2022]
Each automaton state: colored with an RV-LTL value
• Via simple
fi
nal-state reachability checks](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-141-320.jpg)
![Monitoring by coloring automata
[MaggiEtAl,BPM2011] [DeGiacomoEtAl,TOSEM2022]
Each automaton state: colored with an RV-LTL value
• Via simple
fi
nal-state reachability checks](https://image.slidesharecdn.com/declarative-process-mining-pmss-22-220819233800-fbea1644/85/Declarative-process-mining-142-320.jpg)