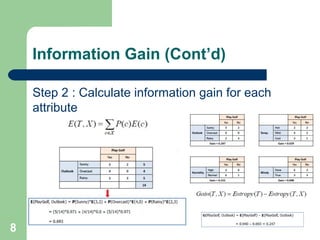
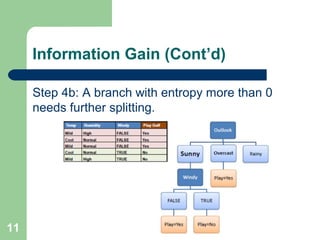
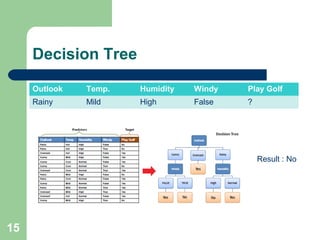
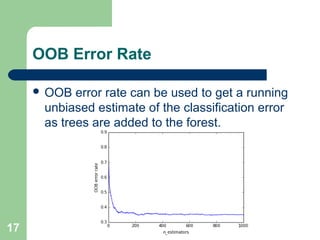
The document discusses decision trees and random forest algorithms. It begins with an outline and defines the problem as determining target attribute values for new examples given a training data set. It then explains key requirements like discrete classes and sufficient data. The document goes on to describe the principles of decision trees, including entropy and information gain as criteria for splitting nodes. Random forests are introduced as consisting of multiple decision trees to help reduce variance. The summary concludes by noting out-of-bag error rate can estimate classification error as trees are added.

1. Decision Tree
&
Random Forest Algorithm
Priagung Khusumanegara
Chonnam National Univeristy

2. Outline
 Introduction
 Example of Decision Tree
 Principles of Decision Tree
– Entropy
– Information gain
 Random Forest
2

3. The problem
 Given a set of training cases/objects and their attribute
values, try to determine the target attribute value of new
examples.
– Classification
– Prediction
3

4. Key Requirements
 Attribute-value description: object or case must be
expressible in terms of a fixed collection of properties or
attributes (e.g., hot, mild, cold).
 Predefined classes (target values): the target
function has discrete output values (bollean or
multiclass)
 Sufficient data: enough training cases should be
provided to learn the model.
4

5. A simple example
5

6. Principled Criterion
 Choosing the most useful attribute for classifying examples.
 Entropy
- A measure of homogeneity of the set of examples
- If the sample is completely homogeneous the entropy is zero and if
the sample is an equally divided it has entropy of one
 Information Gain
- Measures how well a given attribute separates the training
examples according to their target classification
- This measure is used to select among the candidate attributes at
each step while growing the tree
6

7. Information Gain
Step 1 : Calculate entropy of the target
7

8. Information Gain (Cont’d)
Step 2 : Calculate information gain for each
attribute
8

9. Information Gain (Cont’d)
Step 3: Choose attribute with the largest
information gain as the decision node.
9

10. Information Gain (Cont’d)
Step 4a: A branch with entropy of 0 is a leaf
node.
10

11. Information Gain (Cont’d)
Step 4b: A branch with entropy more than 0
needs further splitting.
11

12. Information Gain (Cont’d)
Step 5: The algorithm is run recursively on the
non-leaf branches, until all data is classified.
12

13. Random Forest
 Decision Tree : one tree
 Random Forest : more than one tree
13

14. Decision Tree & Random Forest
14
Decision Tree
Random Forest
Tree 1 Tree 2
Tree 3

15. Decision Tree
Outlook Temp. Humidity Windy Play Golf
Rainy Mild High False ?
15
Result : No

16. Random Forest
16
Tree 1 Tree 2
Tree 3
Tree 1 : No
Tree 2 : No
Tree 3 : Yes
Yes : 1
No : 2
Result : No

17. OOB Error Rate
 OOB error rate can be used to get a running
unbiased estimate of the classification error
as trees are added to the forest.
17