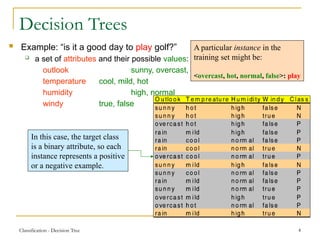
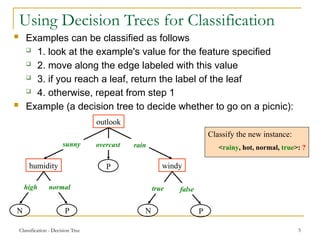
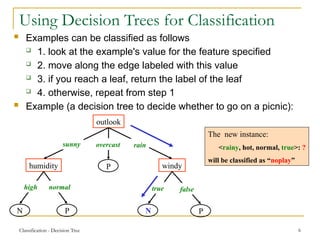
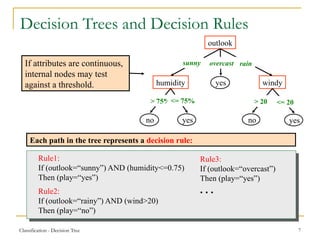
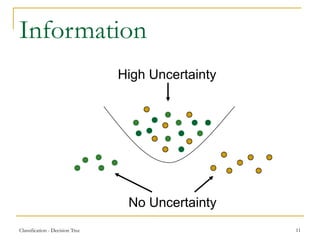
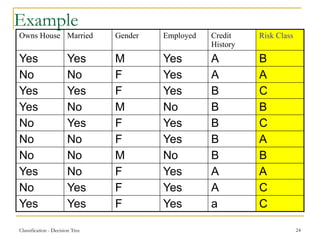
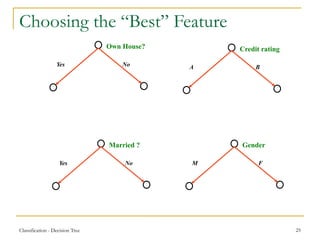
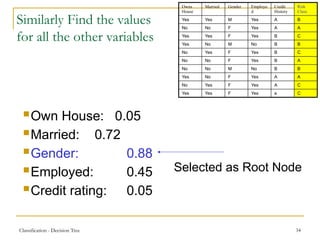
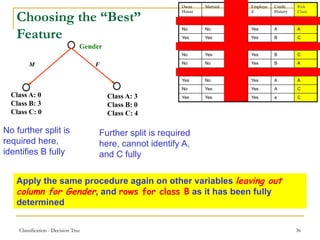
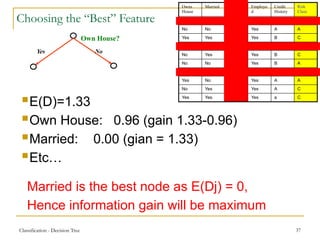
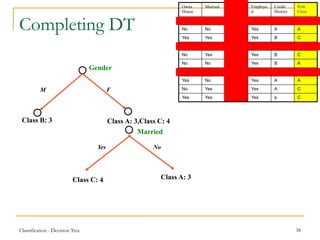
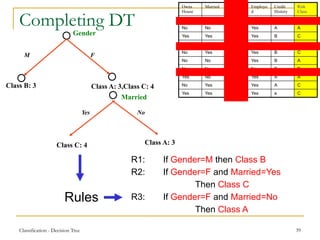
This document discusses decision tree learning, a widely used technique for classification due to its competitive accuracy and efficiency. It explains the structure of decision trees, the process of tree construction and pruning, and how to calculate entropy and information gain to select the best features for classification tasks. Additionally, it illustrates these concepts with examples and mathematical formulations.

1. Supervised Learning:
Classification-I

2. Classification - Decision Tree 2
Decision tree induction

3. Classification - Decision Tree 3
Introduction
 Decision tree learning is one of the most
widely used techniques for classification.
 Its classification accuracy is competitive with
other methods, and
 it is very efficient.
 The classification model is a tree, called
decision tree.
 C4.5 by Ross Quinlan is perhaps the best
known system. It can be downloaded from
the Web.

4. Classification - Decision Tree 4
Decision Trees
 Example: “is it a good day to play golf?”
 a set of attributes and their possible values:
outlook sunny, overcast, rain
temperature cool, mild, hot
humidity high, normal
windy true, false
A particular instance in the
training set might be:
<overcast, hot, normal, false>: play
In this case, the target class
is a binary attribute, so each
instance represents a positive
or a negative example.

5. Classification - Decision Tree 5
Using Decision Trees for Classification
 Examples can be classified as follows
 1. look at the example's value for the feature specified
 2. move along the edge labeled with this value
 3. if you reach a leaf, return the label of the leaf
 4. otherwise, repeat from step 1
 Example (a decision tree to decide whether to go on a picnic):
outlook
humidity windy
P
P N P
N
sunny overcast rain
high normal true false
Classify the new instance:
<rainy, hot, normal, true>: ?

6. Classification - Decision Tree 6
Using Decision Trees for Classification
 Examples can be classified as follows
 1. look at the example's value for the feature specified
 2. move along the edge labeled with this value
 3. if you reach a leaf, return the label of the leaf
 4. otherwise, repeat from step 1
 Example (a decision tree to decide whether to go on a picnic):
outlook
humidity windy
P
P N P
N
sunny overcast rain
high normal true false
The new instance:
<rainy, hot, normal, true>: ?
will be classified as “noplay”

7. Classification - Decision Tree 7
Decision Trees and Decision Rules
outlook
humidity windy
yes
yes no yes
no
sunny overcast rain
> 75%<= 75% > 20 <= 20
If attributes are continuous,
internal nodes may test
against a threshold.
Rule1:
If (outlook=“sunny”) AND (humidity<=0.75)
Then (play=“yes”)
Rule2:
If (outlook=“rainy”) AND (wind>20)
Then (play=“no”)
Rule3:
If (outlook=“overcast”)
Then (play=“yes”)
. . .
Each path in the tree represents a decision rule:

8. Classification - Decision Tree 8
Top-Down Decision Tree Generation
 The basic approach usually consists of two phases:
 Tree construction
 At the start, all the training examples are at the
root
 Partition examples are recursively based on
selected attributes
 Tree pruning
 remove tree branches that may reflect noise in
the training data and lead to errors when
classifying test data
 improve classification accuracy

9. Classification - Decision Tree 9
Top-Down Decision Tree Generation
 Basic Steps in Decision Tree Construction
 Tree starts with a single node representing all data
 If samples are all from the same class then this
node becomes a leaf labeled with class label
 Otherwise, select feature that best separates
samples into individual classes.
 Recursion stops when:
 Samples in node belong to the same class
(majority)
 There are no remaining attributes on which to
split
How to select feature?

10. Classification - Decision Tree 10
How to find Feature to split?
 Many methods are available but our focus
will be on the following two:
 Information Theory
 Gini Index

11. Classification - Decision Tree 11
Information
No Uncertainty
High Uncertainty

12. Classification - Decision Tree 12
Valuable Information
 Which information is more valuable:
 Of high uncertain region, or
 Of no uncertain region
High Uncertain region

13. Classification - Decision Tree 13
Information theory
 Information theory provides a mathematical basis
for measuring the information content.
 To understand the notion of information, think
about it as providing the answer to a question, for
example, whether a coin will come up heads.
 If one already has a good guess about the answer,
then the actual answer is less informative.
 If one already knows that the coin is rigged so that it
will come with heads with probability 0.99, then a
message (advanced information) about the actual
outcome of a flip is worth less than it would be for a
honest coin (50-50).

14. Classification - Decision Tree 14
Information theory (cont …)
 For a fair (honest) coin, you have no
information, and you are willing to pay more
(say in terms of $) for advanced information -
less you know, the more valuable the
information.
 Information theory uses this same intuition,
but instead of measuring the value for
information in dollars, it measures information
contents in bits.
 One bit of information is enough to answer a
yes/no question about which one has no
idea, such as the flip of a fair coin

15. Classification - Decision Tree 15
Information: Basics
 Information (Entropy) is:
 E= - pi log pi,
 where pi is the probability of an event i
 (-pi log pi is always +ve)
 For multiple events
 E(I) = i -pi log pi
 Suppose you toss a fair coin, find the information
(entropy) when the probability of head or tail is 0.5 each.
 possible events: 2, pi=0.5
 E(I)= - 0.5log 0.5 - 0.5log 0.5 = 1.0
 If the coin is biased i.e, chances of heads is 0.75 and of tail
is 0.25, then E(I)= - 0.75log 0.75 - 0.25log 0.25 < 1.0

16. Classification - Decision Tree 16
Information: Basics
 Suppose you have dice and you roll it, find the entropy if
getting a ‘6’ if the probabilities of each event i.e, of getting
1 to 6 is equal.
 possible events: 6, pi=1/6
 E(I)= 6(- 1/6)log (1/6)=2.585
 If the dice is biased i.e, chances of ‘6’ is 0.75 then what is the
entropy:
 p(for 6) =0.75,
 p(for all other) = 0.25,
 p (any other number) = 0.25/5 = 0.05 (equally divided among 1 to 5)
 then E(I)= - 0.75log 0.75 – 5 (0.05)log (0.05) = 1.39

17. Classification - Decision Tree 17
Information: Basics
 Suppose you have dice and you roll it, find the entropy if
getting a ‘6’ if the probabilities of each event i.e, of getting
1 to 6 is equal.
 possible events: 6, pi=1/6
 E(I)= 6(- 1/6)log (1/6)=2.585
 If the dice is biased i.e, chances of ‘6’ is 0.75 then what is the
entropy:
 p(for 6) =0.75,
 p(for all other) = 0.25,
 p (any other number) = 0.25/5 = 0.05 (equally divided among 1 to 5)
 then E(I)= - 0.75log 0.75 – 5 (0.05)log (0.05) = 1.39
As the probability of an event increases uncertainty
reduces so the entropy is also lower

18. Classification - Decision Tree 18
Information: Basics
 Suppose you have dice and you roll it, find the entropy if
getting a ‘6’ if the probabilities of each event i.e, of getting
1 to 6 is equal.
 possible events: 6, pi=1/6
 E(I)= 6(- 1/6)log (1/6)=2.585
 If the dice is biased i.e, chances of ‘6’ is 0.75 then what is the
entropy:
 p(for 6) =0.75,
 p(for all other) = 0.25,
 p (any other number) = 0.25/5 = 0.05 (equally divided among 1 to 5)
 then E(I)= - 0.75log 0.75 – 5 (0.05)log (0.05) = 1.39
So in making a decision tree
choose a variable as the feature variable
that reduces the uncertainty once its value is known

19. Classification - Decision Tree 19
DT: Entropy – A measuring Value
 Entropy is a concept originated in thermodynamics
but later found its way to information theory.
 In decision tree construction process, definition of
entropy as a measure of disorder suits well.
 If the class values of the data in a node is equally
divided among possible values of the class value,
we say entropy (disorder) is maximum.
 If the class values of the data in a node is same for
all data, entropy (disorder) is minimum.

20. Classification - Decision Tree 20
Information theory: Entropy measure
 The entropy formula,
 Pr(cj) is the probability of class cj in data set D
 We use entropy as a measure of impurity or
disorder of data set D. (or, a measure of
information in a tree)
,
1
)
Pr(
)
Pr(
log
)
Pr(
)
(
|
|
1
|
|
1
2







C
j
j
j
C
j
j
c
c
c
D
entropy

21. Classification - Decision Tree 21
Entropy measure:
 As the data become purer and purer, the entropy value
becomes smaller and smaller. This is useful for classification
E= - (p /s)log(p /s) - (n /s)log(n /s)
p= all +ve examples, n= -ve, s=total examples

22. Classification - Decision Tree 22
Information gain
 Given a set of examples D, we first compute its
entropy for the ‘c’ classes:
 If we choose attribute Ai, with v values, the root of the
current tree, this will partition D into v subsets D1, D2
…, Dv . The expected entropy if Ai is used as the
current root:




v
j
j
j
A D
entropy
D
D
D
entropy i
1
)
(
|
|
|
|
)
(
)
Pr(
log
)
Pr(
)
(
|
|
1
2 j
C
j
j c
c
D
entropy 




23. Classification - Decision Tree 23
Information gain (cont …)
 Information gained by selecting attribute Ai to
branch or to partition the data is
 We choose the attribute with the highest gain to
branch/split the current tree.
 As the information gain increases for a variable,
the uncertainty in decision making reduces.
)
(
)
(
)
,
( D
entropy
D
entropy
A
D
gain i
A
i 


24. Classification - Decision Tree 24
Example
Owns House Married Gender Employed Credit
History
Risk Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

25. Classification - Decision Tree 25
Choosing the “Best” Feature
Gender
M F
Married ?
Yes No
Credit rating
A B
Own House?
Yes No

26. Classification - Decision Tree 26
Choosing the “Best” Feature
Own House?
Yes No
 Find the overall entropy first:
 Total samples: 10
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

27. Classification - Decision Tree 27
Choosing the “Best” Feature
Own House?
Yes No
 Find the overall entropy first:
 Total samples: 10
 Class A: 3, Class B: 3, Class C: 4
 Entropy(D)= -(3/10)log(3/10)-(3/10)log(3/10)-(4/10)log(4/10) = 1.57
 Own homes: has two v values, Yes (5 instances) and No (5
instances), total 10, probability of each is 0.5
 Find entropy(Dj) for each yes and no and the add the two weighted
by their class probabilities
 E(yes)= -(1/5)log(1/5) - (2/5)log(2/5) -(2/5)log(2/5) = 1.52
 E(no)= -(2/5)log(2/5) - (1/5)log(1/5) -(2/5)log(2/5) = 1.52
 E(Dj) = 0.5*E(yes)+0.5*E(no) = 1.52
 Gain(D, Own House) = 1.57-1.52 = 0.05
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

28. Classification - Decision Tree 28
Choosing the “Best” Feature
Own House?
Yes No
 Find the overall entropy first:
 Total samples: 10
 Class A: 3, Class B: 3, Class C: 4
 Entropy(D)= -(3/10)log(3/10)-(3/10)log(3/10)-(4/10)log(4/10) = 1.57
 Own homes: has two v values, Yes (5 instances) and No (5
instances), total 10, probability of each is 0.5
 Find entropy(Dj) for each yes and no and the add the two weighted
by their class probabilities
 E(yes)= -(1/5)log(1/5) - (2/5)log(2/5) -(2/5)log(2/5) = 1.52
 E(no)= -(2/5)log(2/5) - (1/5)log(1/5) -(2/5)log(2/5) = 1.52
 E(Dj) = 0.5*E(yes)+0.5*E(no) = 1.52
 Gain(D, Own House) = 1.57-1.52 = 0.05
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

29. Classification - Decision Tree 29
Choosing the “Best” Feature
Own House?
Yes No
 Find the overall entropy first:
 Total samples: 10
 Class A: 3, Class B: 3, Class C: 4
 Entropy(D)= -(3/10)log(3/10)-(3/10)log(3/10)-(4/10)log(4/10) = 1.57
 Own homes: has two v values, Yes (5 instances) and No (5
instances), total samples 10, probability of each is 0.5
 Find entropy(Dj) for each yes and no and the add the two weighted
by their class probabilities
 E(yes)= -(1/5)log(1/5) - (2/5)log(2/5) -(2/5)log(2/5) = 1.52
 E(no)= -(2/5)log(2/5) - (1/5)log(1/5) -(2/5)log(2/5) = 1.52
 E(Dj) = 0.5*E(yes)+0.5*E(no) = 1.52
 Gain(D, Own House) = 1.57-1.52 = 0.05
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

30. Classification - Decision Tree 30
Choosing the “Best” Feature
Own House?
Yes No
 Find the overall entropy first:
 Total samples: 10
 Class A: 3, Class B: 3, Class C: 4
 Entropy(D)= -(3/10)log(3/10)-(3/10)log(3/10)-(4/10)log(4/10) = 1.57
 Own homes: has two v values, Yes (5 instances) and No (5
instances), total 10, probability of each is 0.5
 Find entropy(Dj) for each yes and no and the add the two weighted
by their class probabilities
 E(yes)= -(1/5)log(1/5) - (2/5)log(2/5) -(2/5)log(2/5) = 1.52
 E(no)= -(2/5)log(2/5) - (1/5)log(1/5) -(2/5)log(2/5) = 1.52
 E(Dj) = 0.5*E(yes)+0.5*E(no) = 1.52
 Gain(D, Own House) = 1.57-1.52 = 0.05
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C
Only 1 out of 5 have class A for own house: yes
Only 2 out of 5 have class B for own house: yes
Only 2 out of 5 have class C for own house: yes

31. Classification - Decision Tree 31
Choosing the “Best” Feature
Own House?
Yes No
 Find the overall entropy first:
 Total samples: 10
 Class A: 3, Class B: 3, Class C: 4
 Entropy(D)= -(3/10)log(3/10)-(3/10)log(3/10)-(4/10)log(4/10) = 1.57
 Own homes: has two v values, Yes (5 instances) and No (5
instances), total 10, probability of each is 0.5
 Find entropy(Dj) for each yes and no and the add the two weighted
by their class probabilities
 E(yes)= -(1/5)log(1/5) - (2/5)log(2/5) -(2/5)log(2/5) = 1.52
 E(no)= -(2/5)log(2/5) - (1/5)log(1/5) -(2/5)log(2/5) = 1.52
 E(Dj) = 0.5*E(yes)+0.5*E(no) = 1.52
 Gain(D, Own House) = 1.57-1.52 = 0.05
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

32. Classification - Decision Tree 32
Choosing the “Best” Feature
Own House?
Yes No
 Find the overall entropy first:
 Total samples: 10
 Class A: 3, Class B: 3, Class C: 4
 Entropy(D)= -(3/10)log(3/10)-(3/10)log(3/10)-(4/10)log(4/10) = 1.57
 Own homes: has two v values, Yes (5 instances) and No (5
instances), total 10, probability of each is 0.5
 Find entropy(Dj) for each yes and no and the add the two weighted
by their class probabilities
 E(yes)= -(1/5)log(1/5) - (2/5)log(2/5) -(2/5)log(2/5) = 1.52
 E(no)= -(2/5)log(2/5) - (1/5)log(1/5) -(2/5)log(2/5) = 1.52
 E(Dj) = 0.5*E(yes)+0.5*E(no) = 1.52
 Gain(D, Own House) = 1.57-1.52 = 0.05
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

33. Classification - Decision Tree 33
Choosing the “Best” Feature
Own House?
Yes No
 Find the overall entropy first:
 Total samples: 10
 Class A: 3, Class B: 3, Class C: 4
 Entropy(D)= -(3/10)log(3/10)-(3/10)log(3/10)-(4/10)log(4/10) = 1.57
 Own homes: has two v values, Yes (5 instances) and No (5
instances), total 10, probability of each is 0.5
 Find entropy(Dj) for each yes and no and the add the two weighted
by their class probabilities
 E(yes)= -(1/5)log(1/5) - (2/5)log(2/5) -(2/5)log(2/5) = 1.52
 E(no)= -(2/5)log(2/5) - (1/5)log(1/5) -(2/5)log(2/5) = 1.52
 E(Dj) = 0.5*E(yes)+0.5*E(no) = 1.52
 Gain(D, Own House) = 1.57-1.52 = 0.05
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

34. Classification - Decision Tree 34
Similarly Find the values
for all the other variables
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C
Own House: 0.05
Married: 0.72
Gender: 0.88
Employed: 0.45
Credit rating: 0.05
Selected as Root Node

35. Classification - Decision Tree 35
Choosing the “Best”
Feature
Gender
M F
Class A: 3
Class B: 0
Class C: 4
Class A: 0
Class B: 3
Class C: 0
No further split is
required here,
identifies B fully
Further split is required
here, cannot identify A,
and C fully
Apply the same procedure again on other variables leaving out
column for Gender, and rows for class B as it has been fully
determined
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

36. Classification - Decision Tree 36
Choosing the “Best”
Feature
Gender
M F
Class A: 3
Class B: 0
Class C: 4
Class A: 0
Class B: 3
Class C: 0
No further split is
required here,
identifies B fully
Further split is required
here, cannot identify A,
and C fully
Apply the same procedure again on other variables leaving out
column for Gender, and rows for class B as it has been fully
determined
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C

37. Classification - Decision Tree 37
Choosing the “Best” Feature
Own House?
Yes No
E(D)=1.33
Own House: 0.96 (gain 1.33-0.96)
Married: 0.00 (gian = 1.33)
Etc…
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C
Married is the best node as E(Dj) = 0,
Hence information gain will be maximum

38. Classification - Decision Tree 38
Completing DT
Gender
M F
Class A: 3,Class C: 4
Class B: 3
Married
Yes No
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C
Class C: 4 Class A: 3

39. Classification - Decision Tree 39
Completing DT
Owns
House
Married Gender Employe
d
Credit
History
Risk
Class
Yes Yes M Yes A B
No No F Yes A A
Yes Yes F Yes B C
Yes No M No B B
No Yes F Yes B C
No No F Yes B A
No No M No B B
Yes No F Yes A A
No Yes F Yes A C
Yes Yes F Yes a C
Gender
M F
Class A: 3,Class C: 4
Class B: 3
Married
Yes No
Class C: 4 Class A: 3
Rules
R1: If Gender=M then Class B
R2: If Gender=F and Married=Yes
Then Class C
R3: If Gender=F and Married=No
Then Class A

40. Classification - Decision Tree 40
Trees Construction Algorithm (ID3)
 Decision Tree Learning Method (ID3)
 Input: a set of examples S, a set of features F, and a target set T (target
class T represents the type of instance we want to classify, e.g., whether
“to play golf”)
 1. If every element of S is already in T, return “yes”; if no element of S is in
T return “no”
 2. Otherwise, choose the best feature f from F (if there are no features
remaining, then return failure);
 3. Extend tree from f by adding a new branch for each attribute value
 4. Distribute training examples to leaf nodes (so each leaf node S is now
the set of examples at that node, and F is the remaining set of features not
yet selected)
 5. Repeat steps 1-5 for each leaf node
 Main Question:
 how do we choose the best feature at each step?
Note: ID3 algorithm only deals with categorical attributes, but can be extended
(as in C4.5) to handle continuous attributes