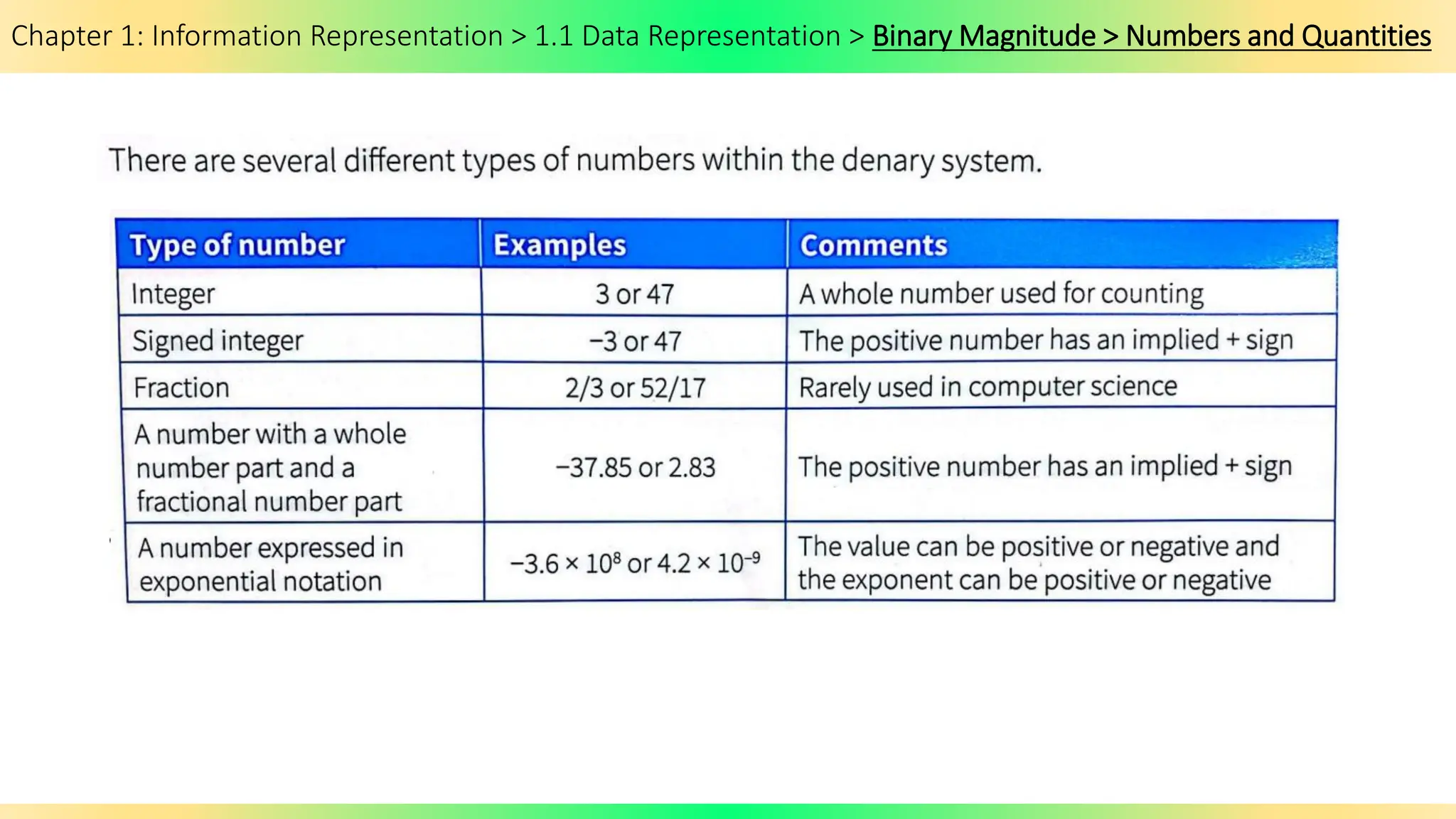
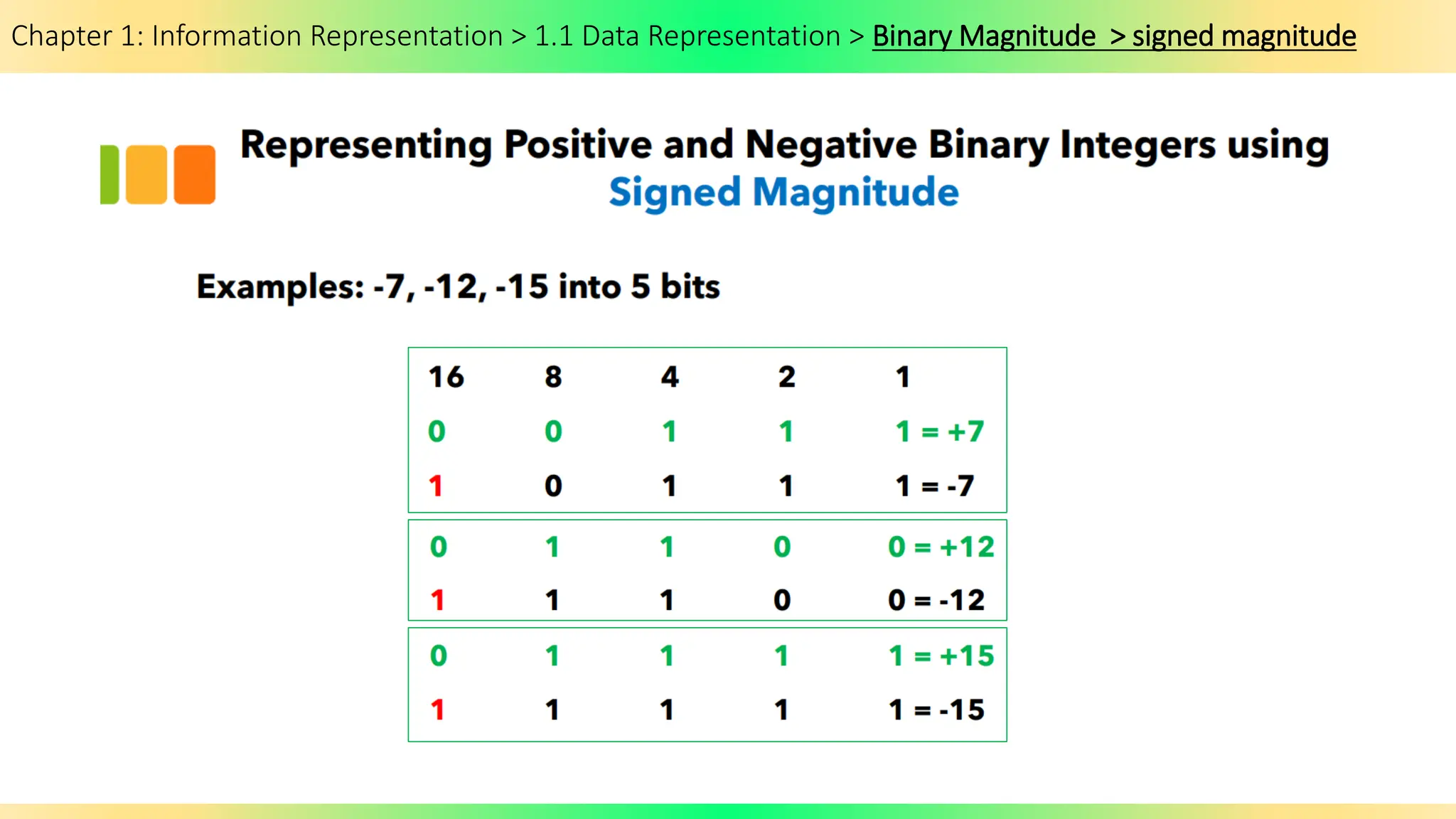
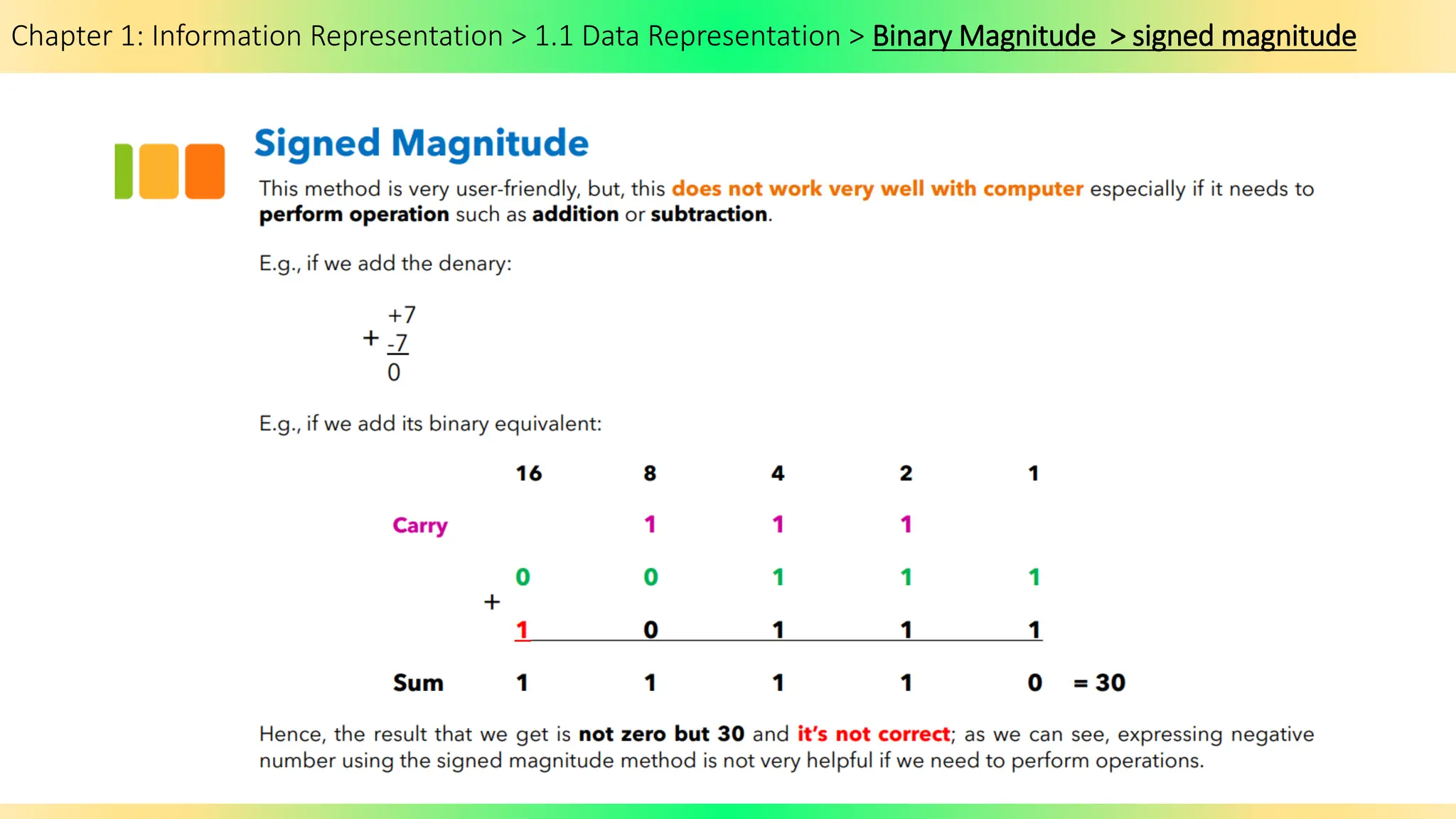
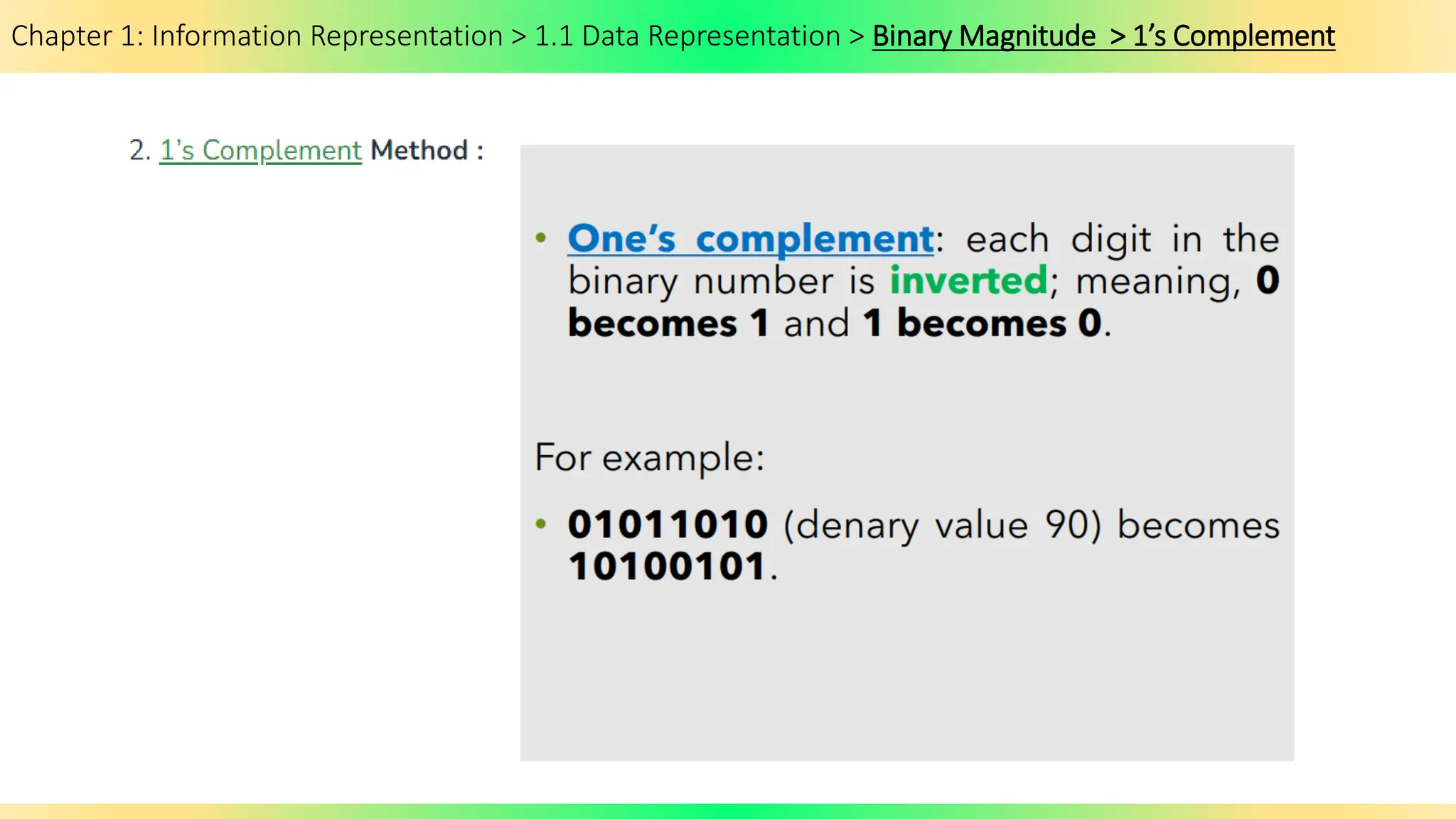
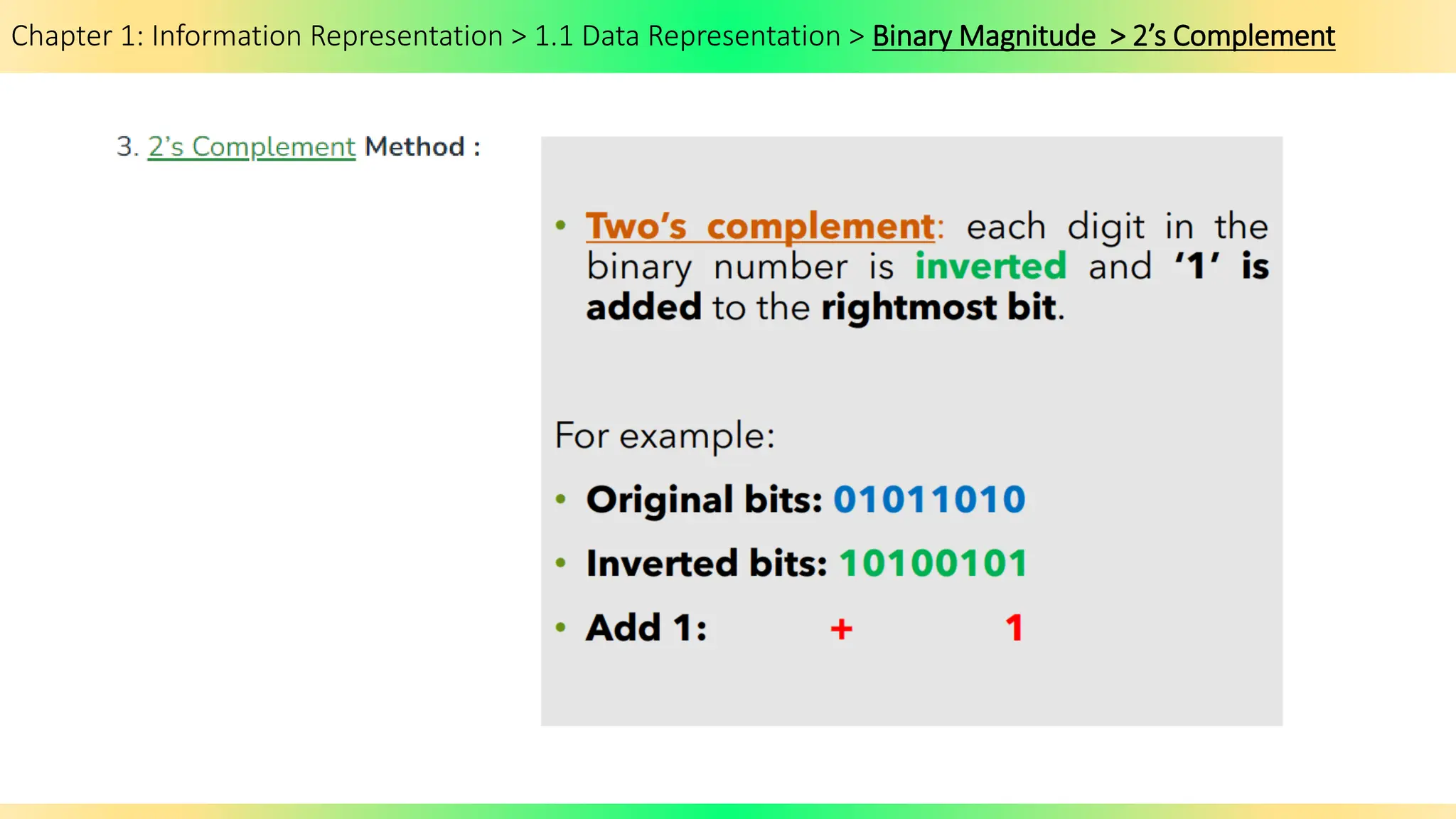
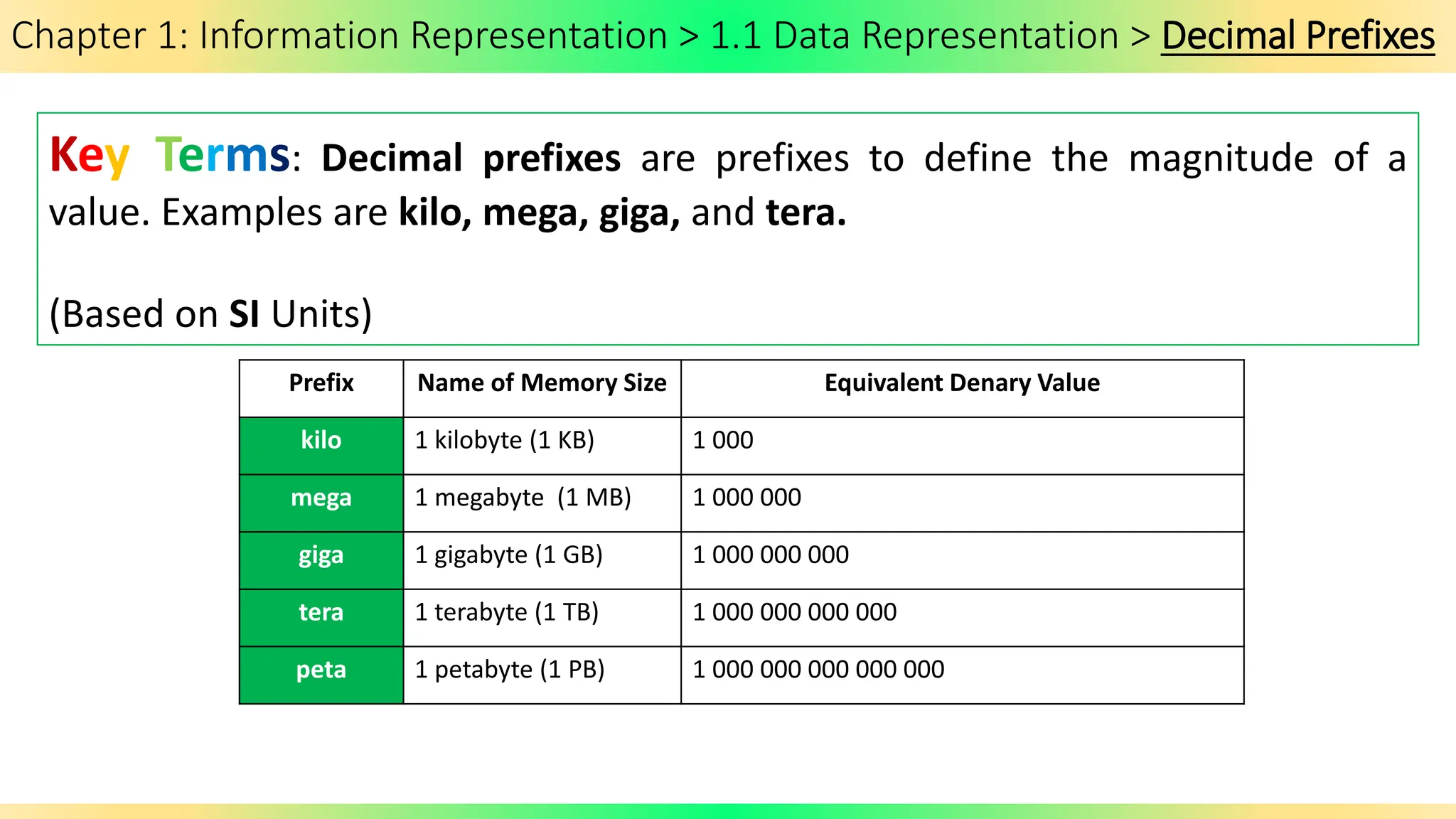
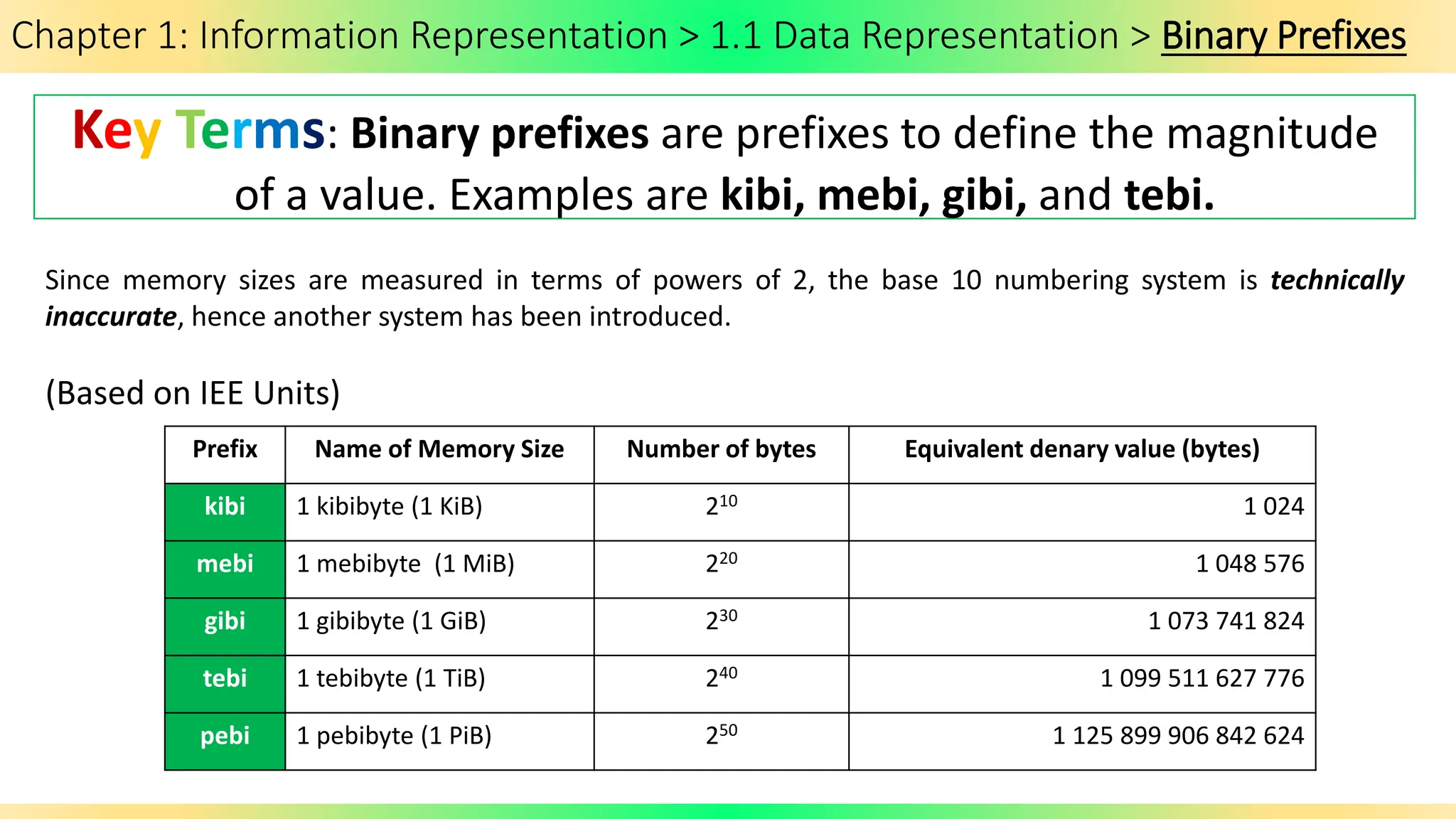
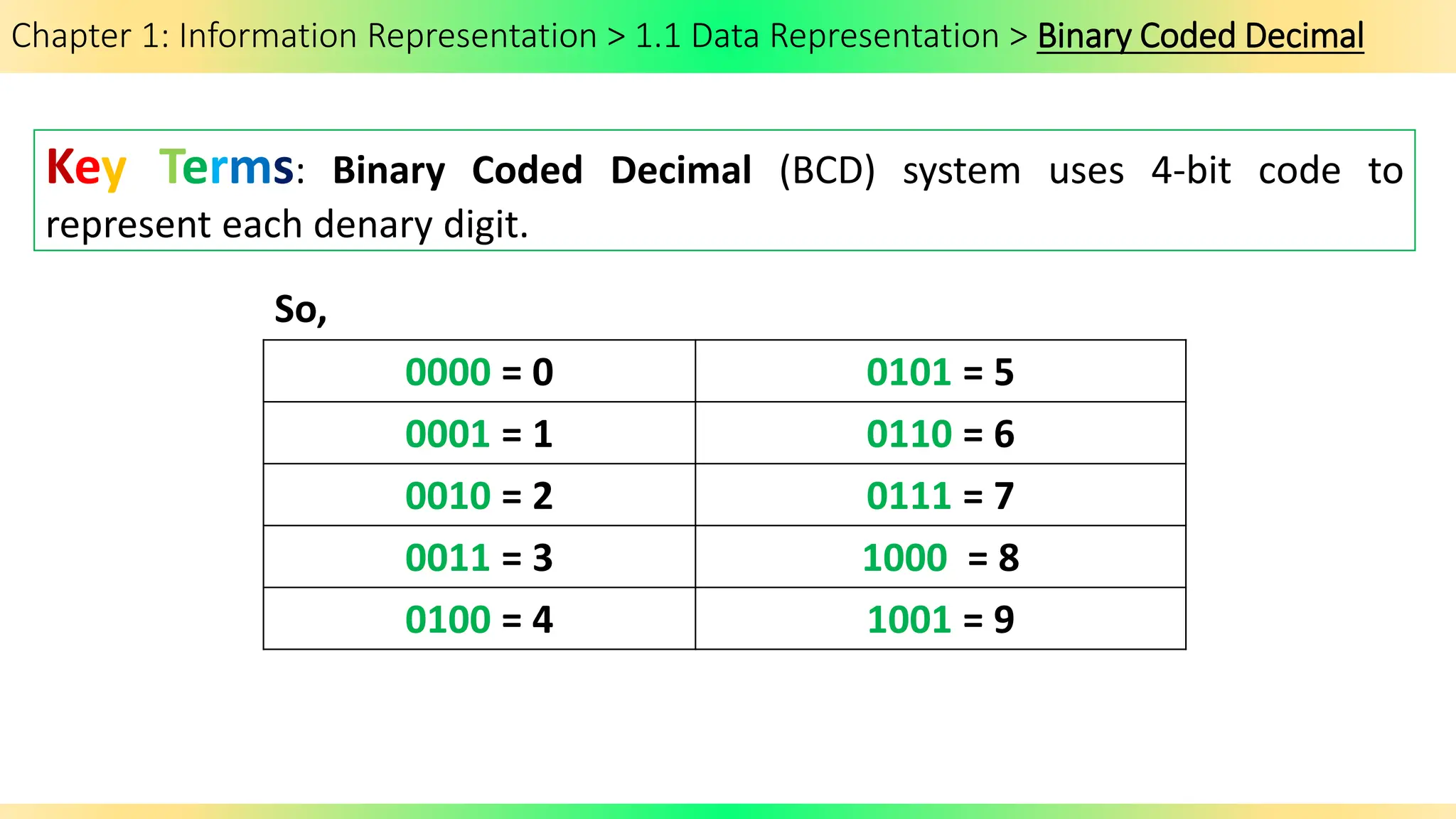
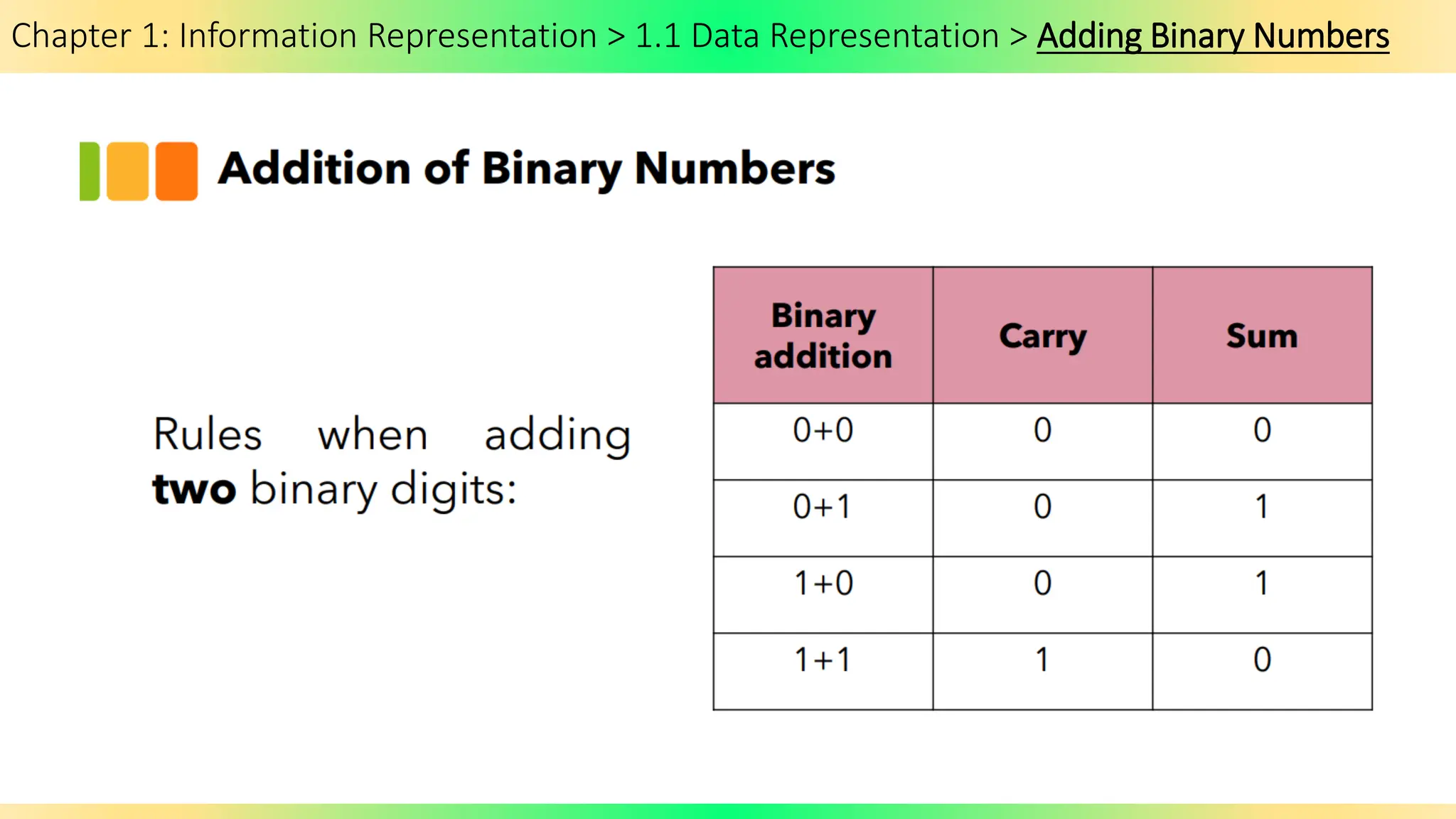
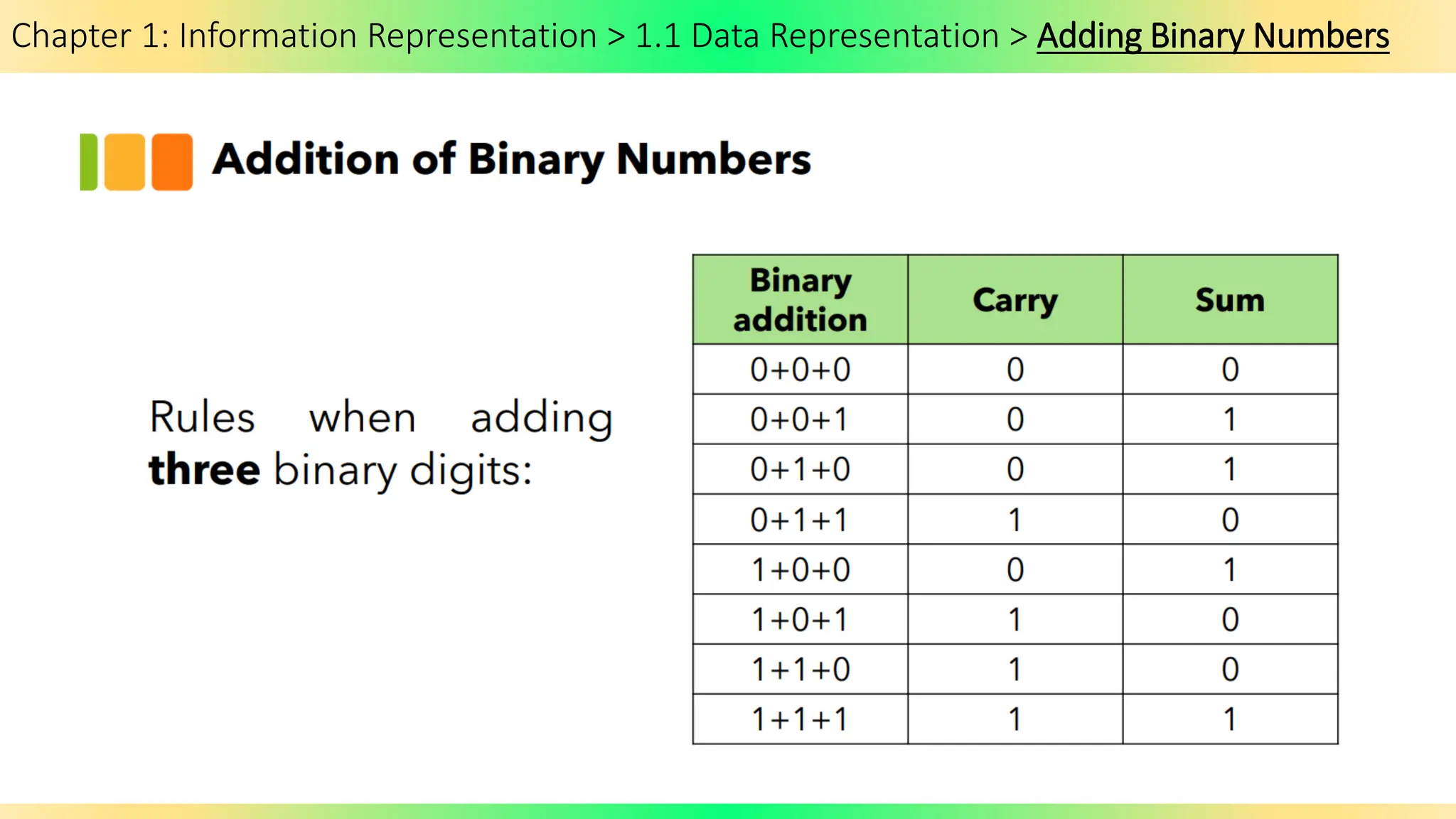
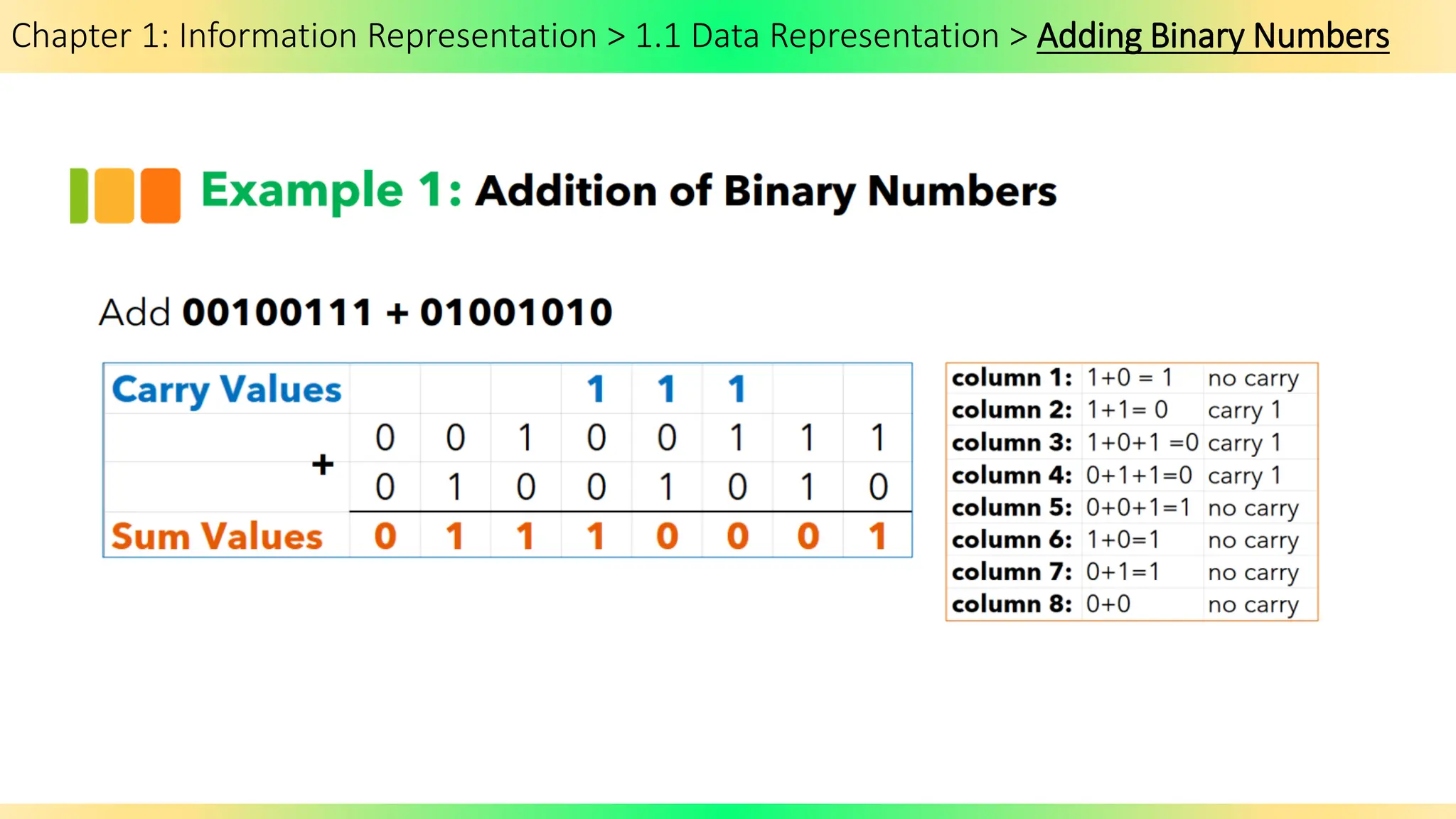
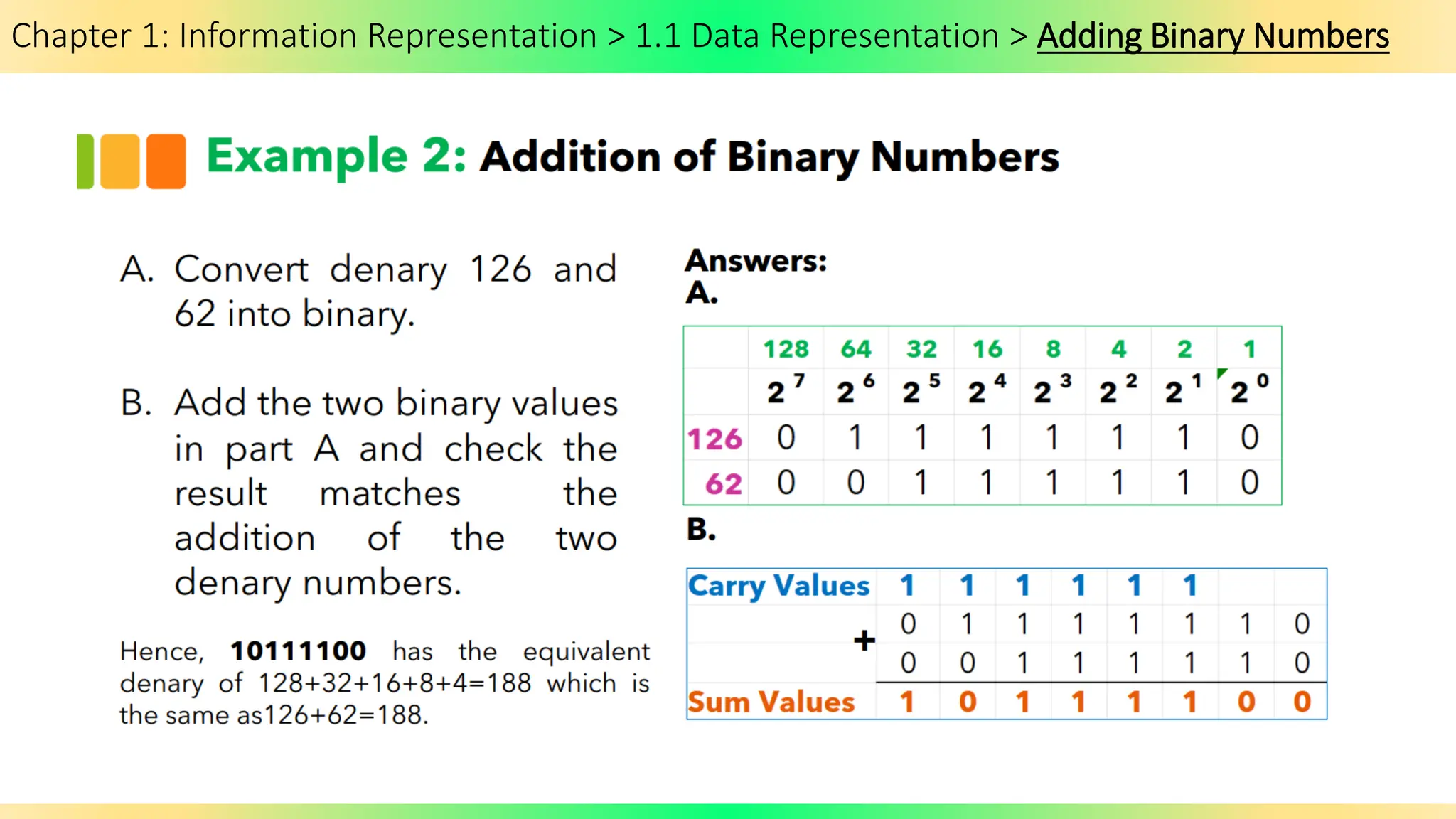
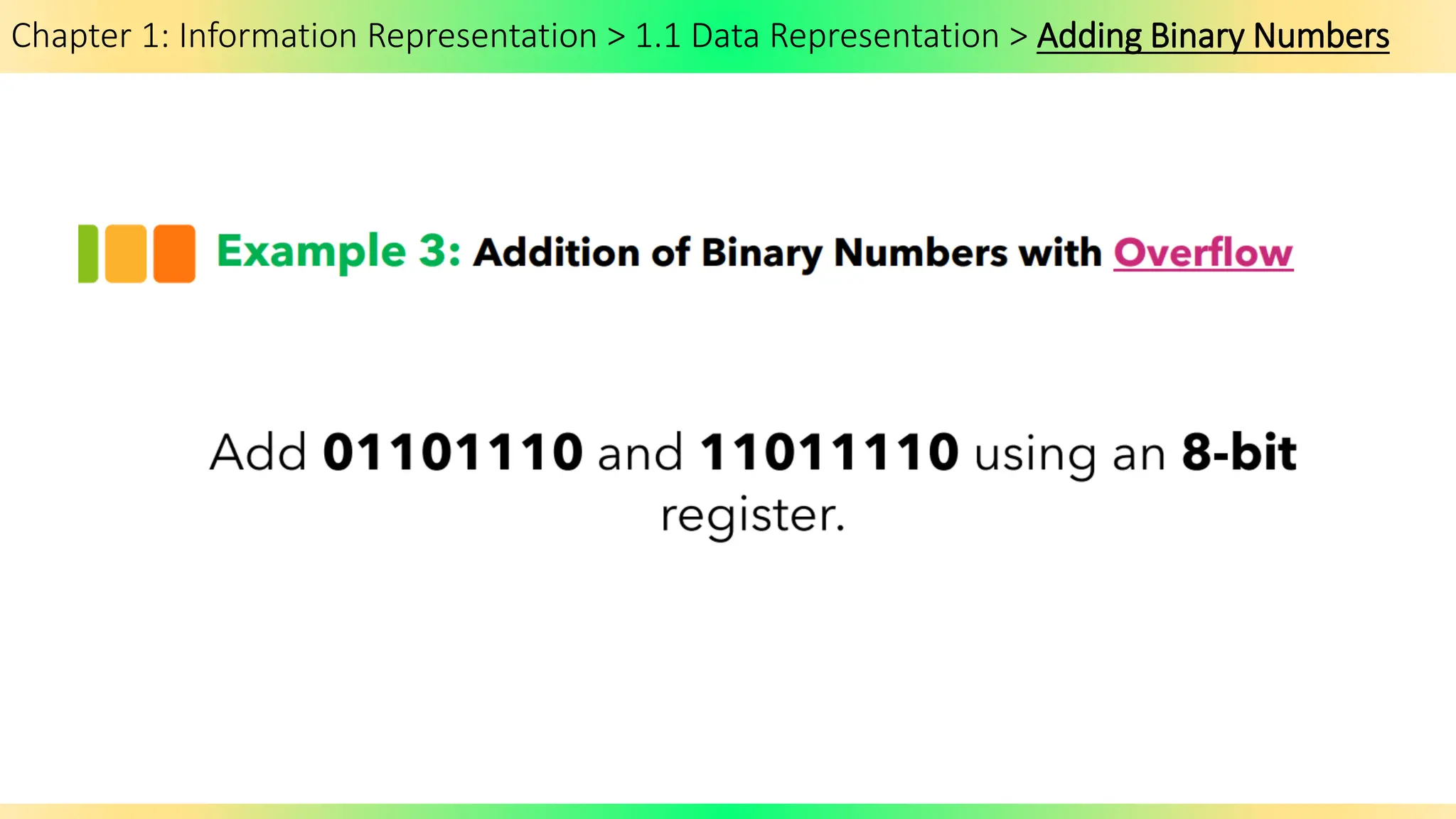
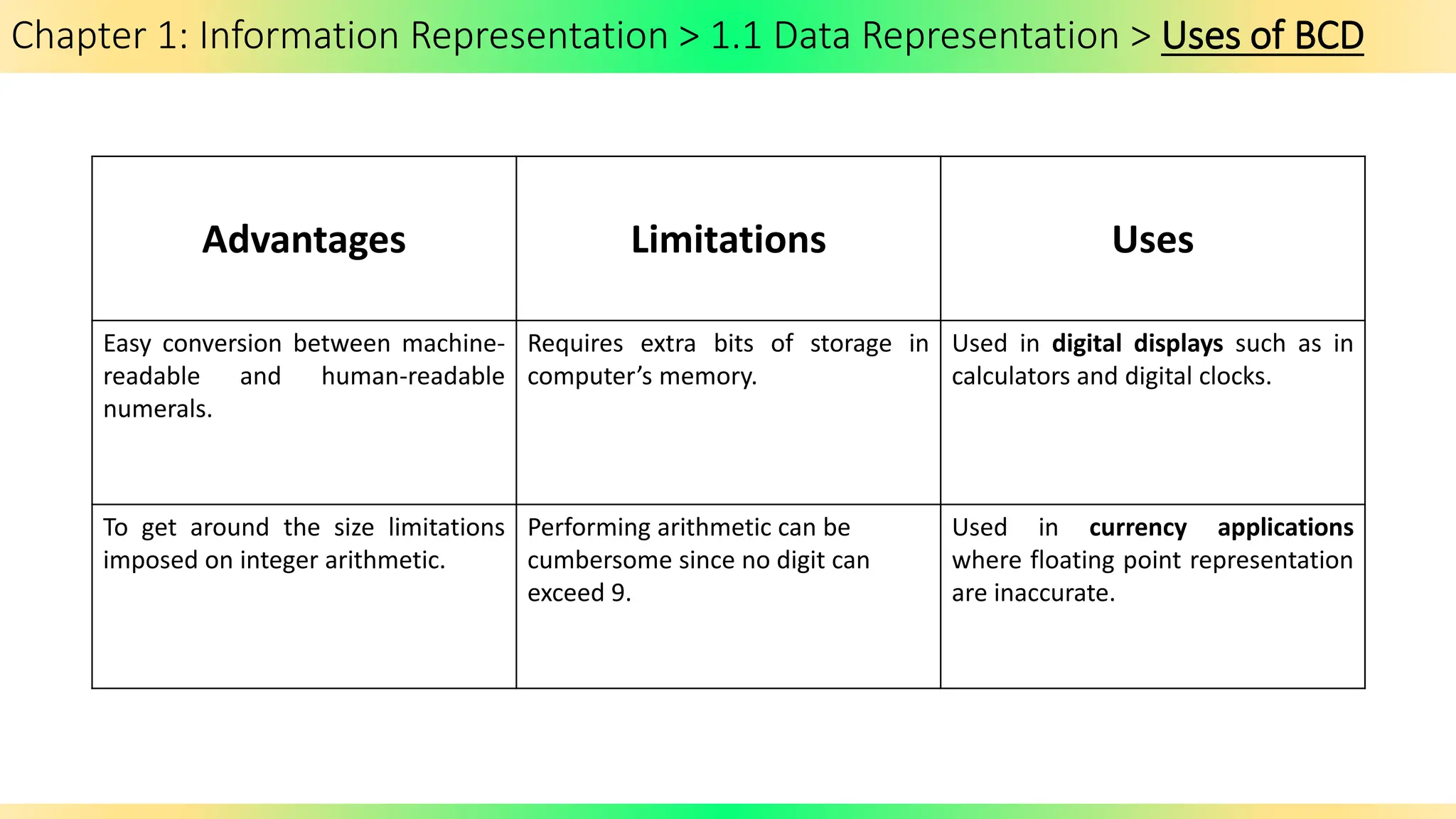
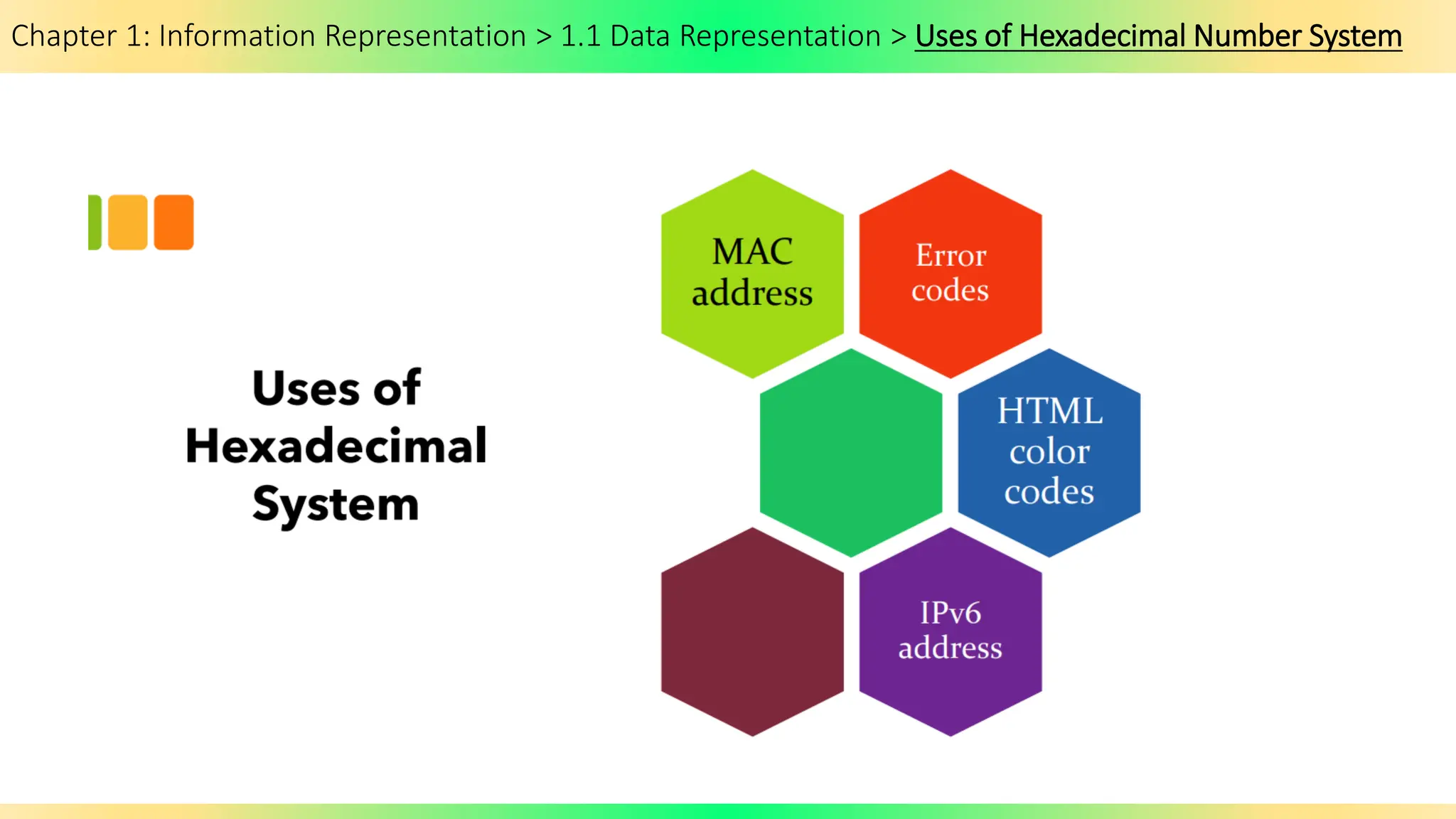
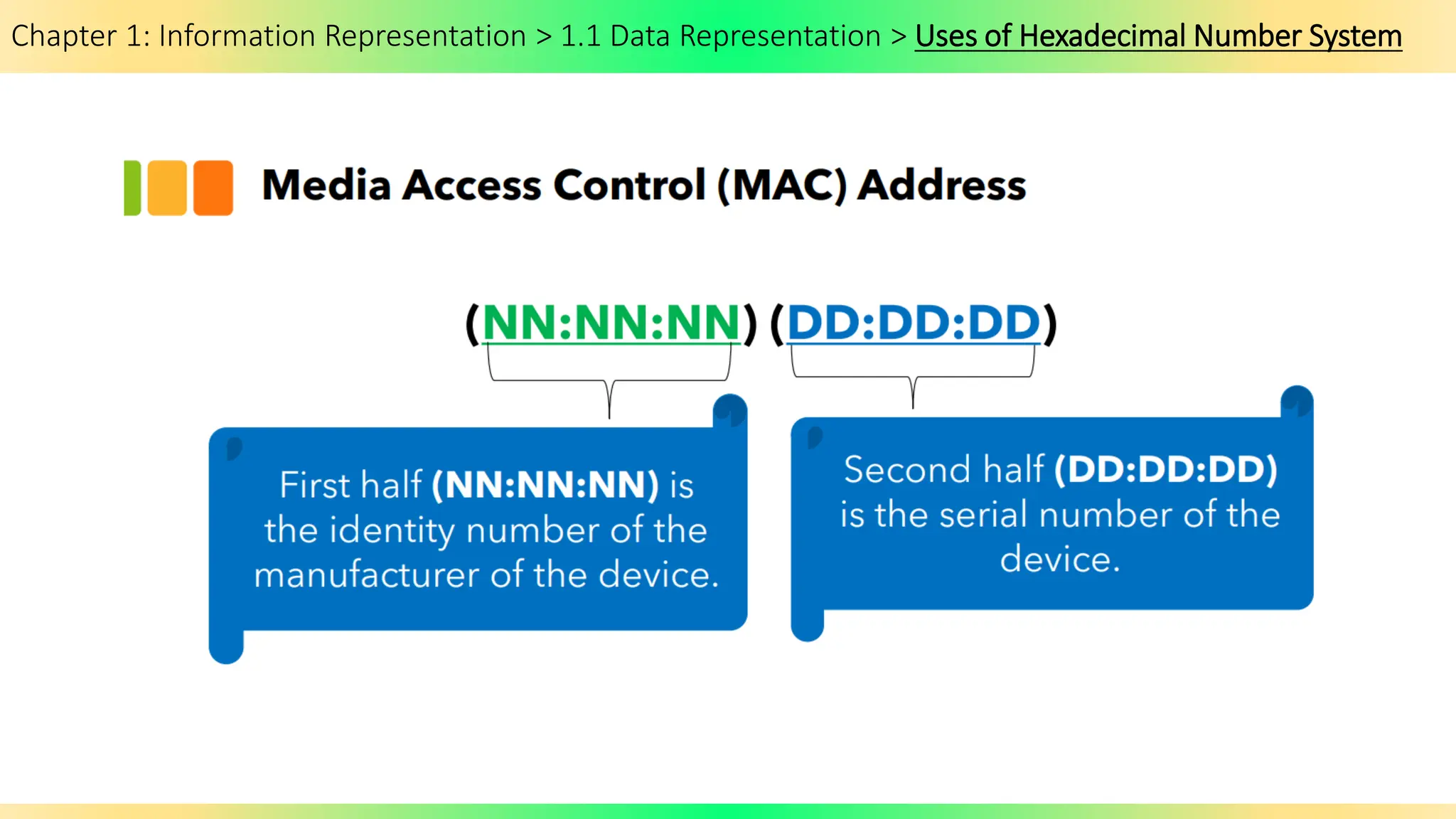
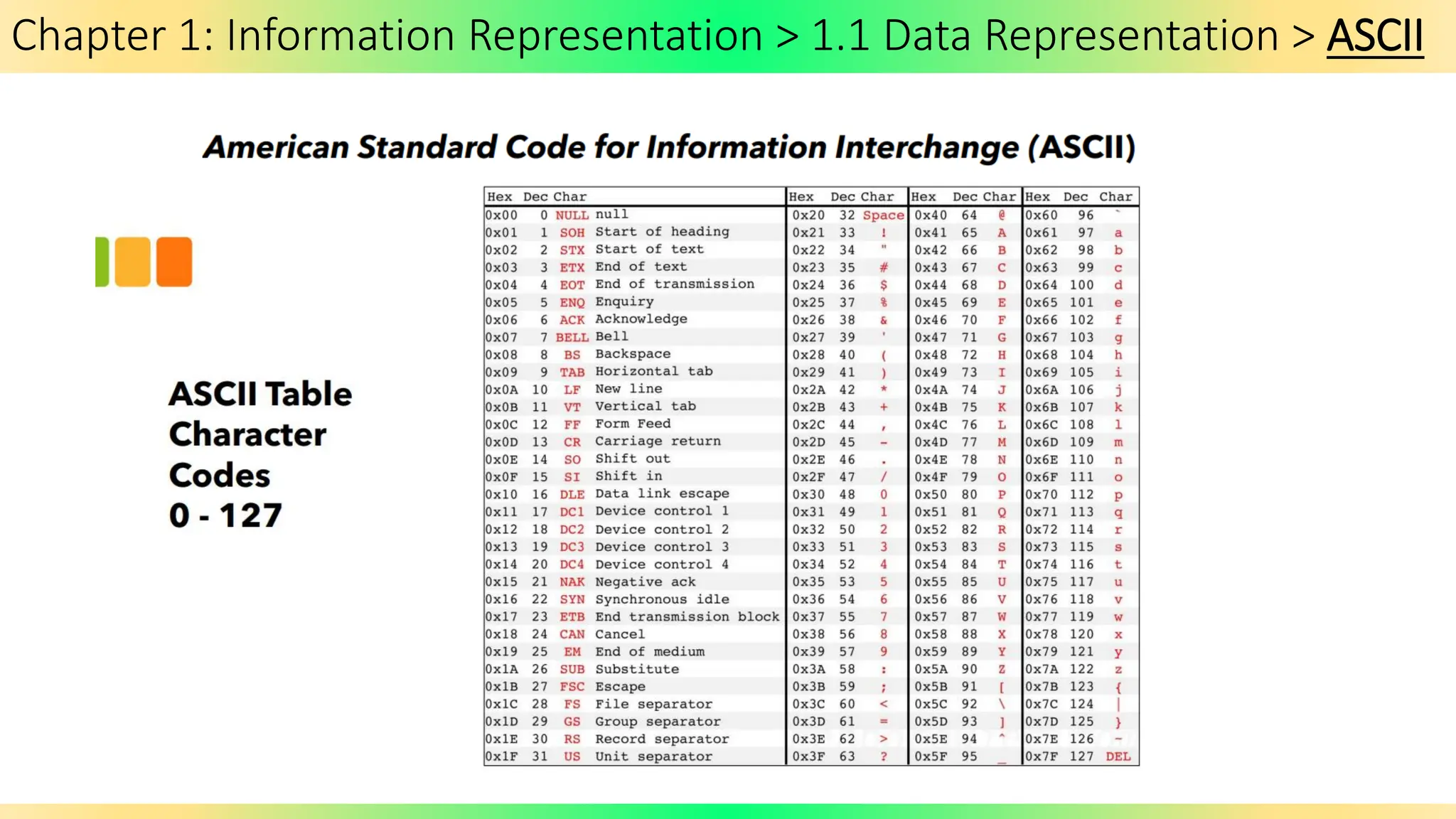
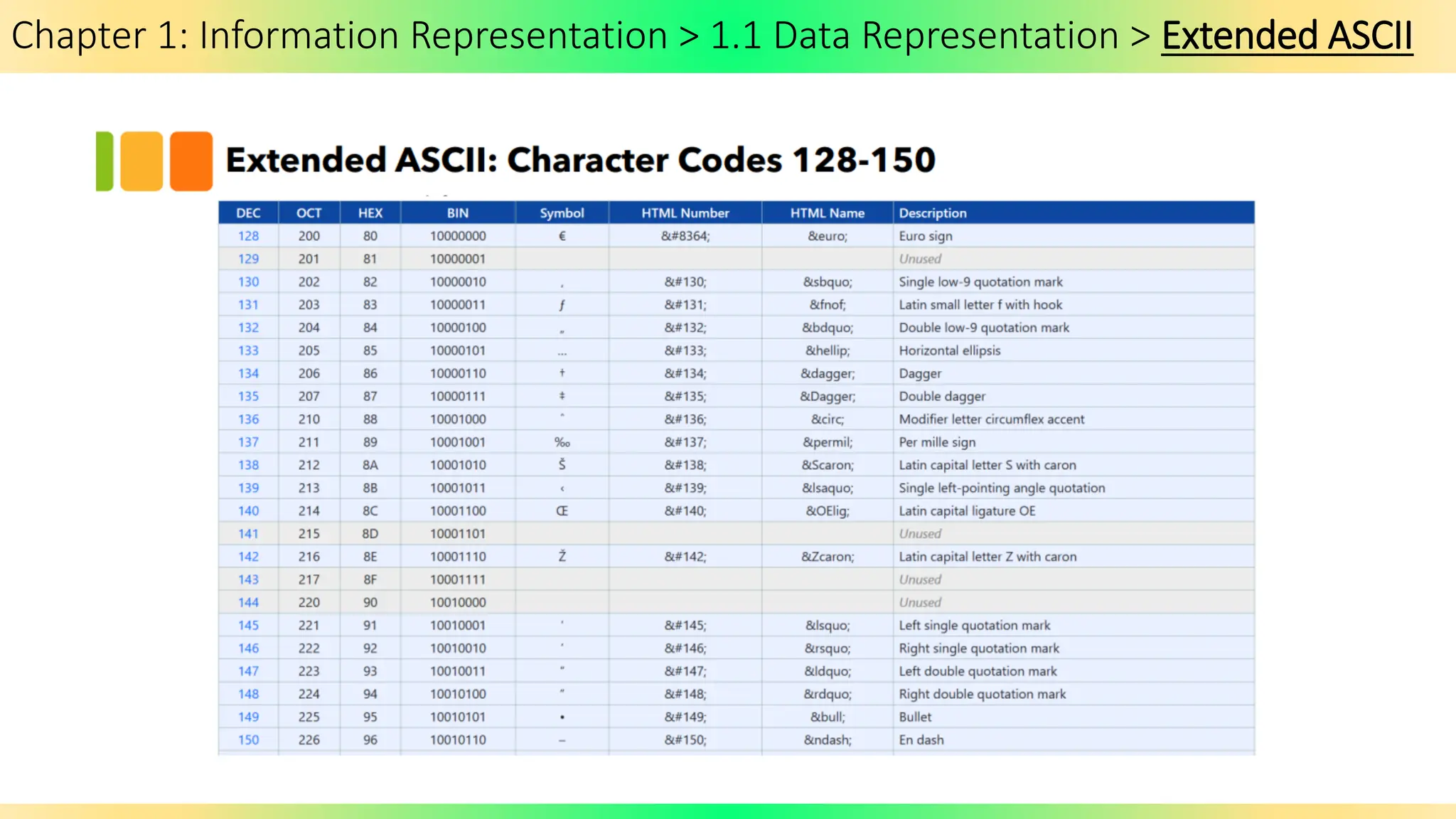
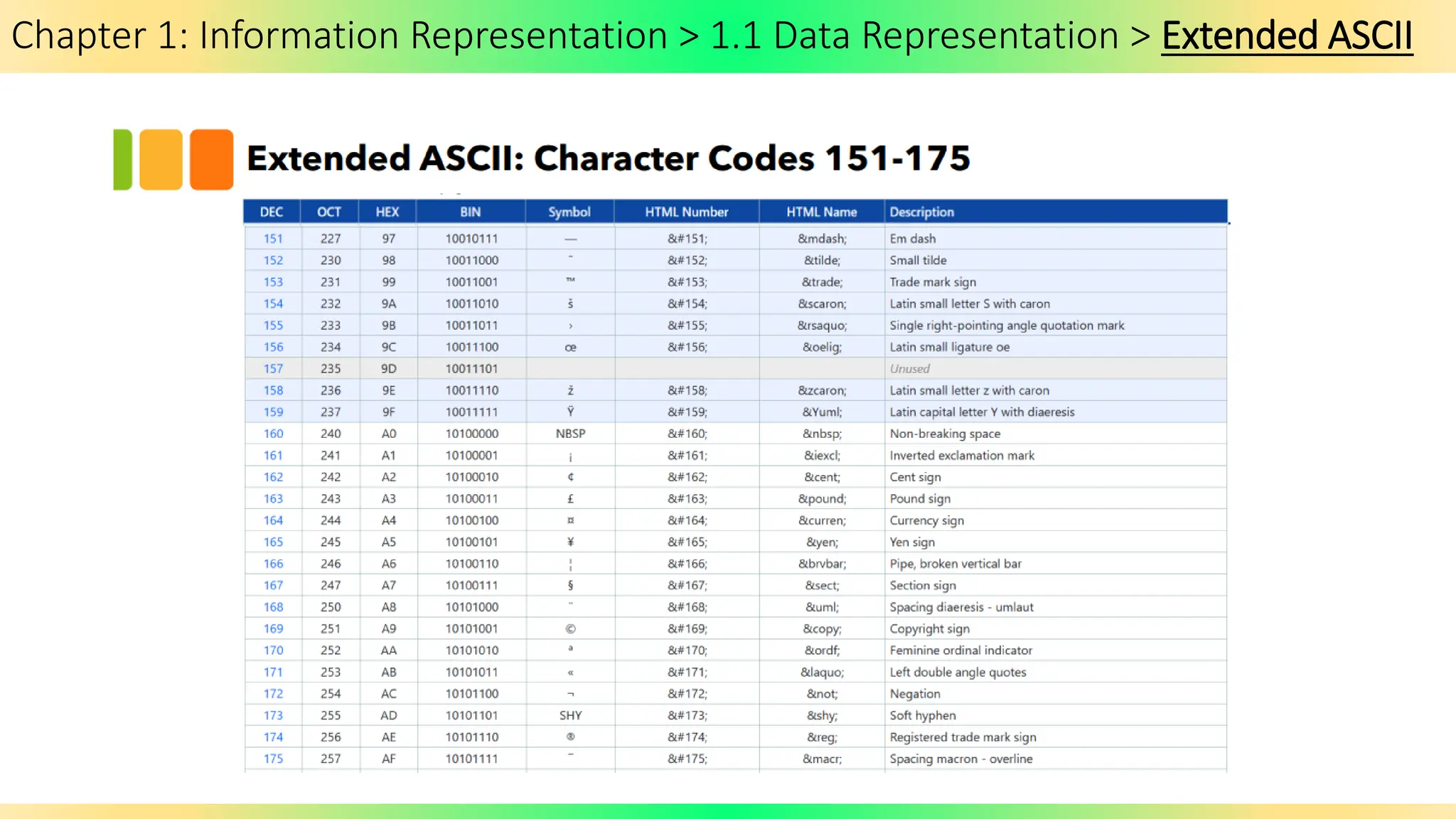
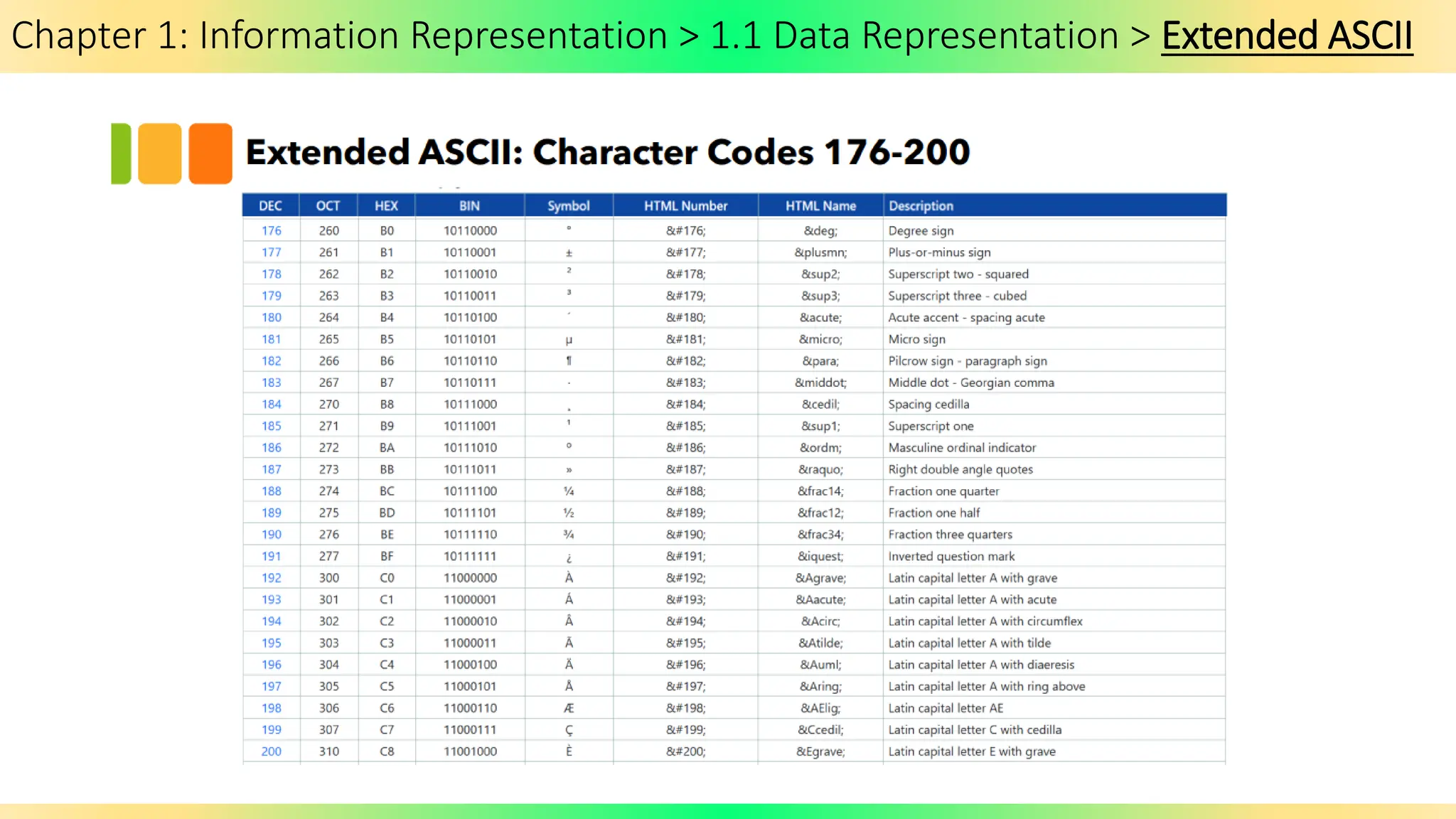
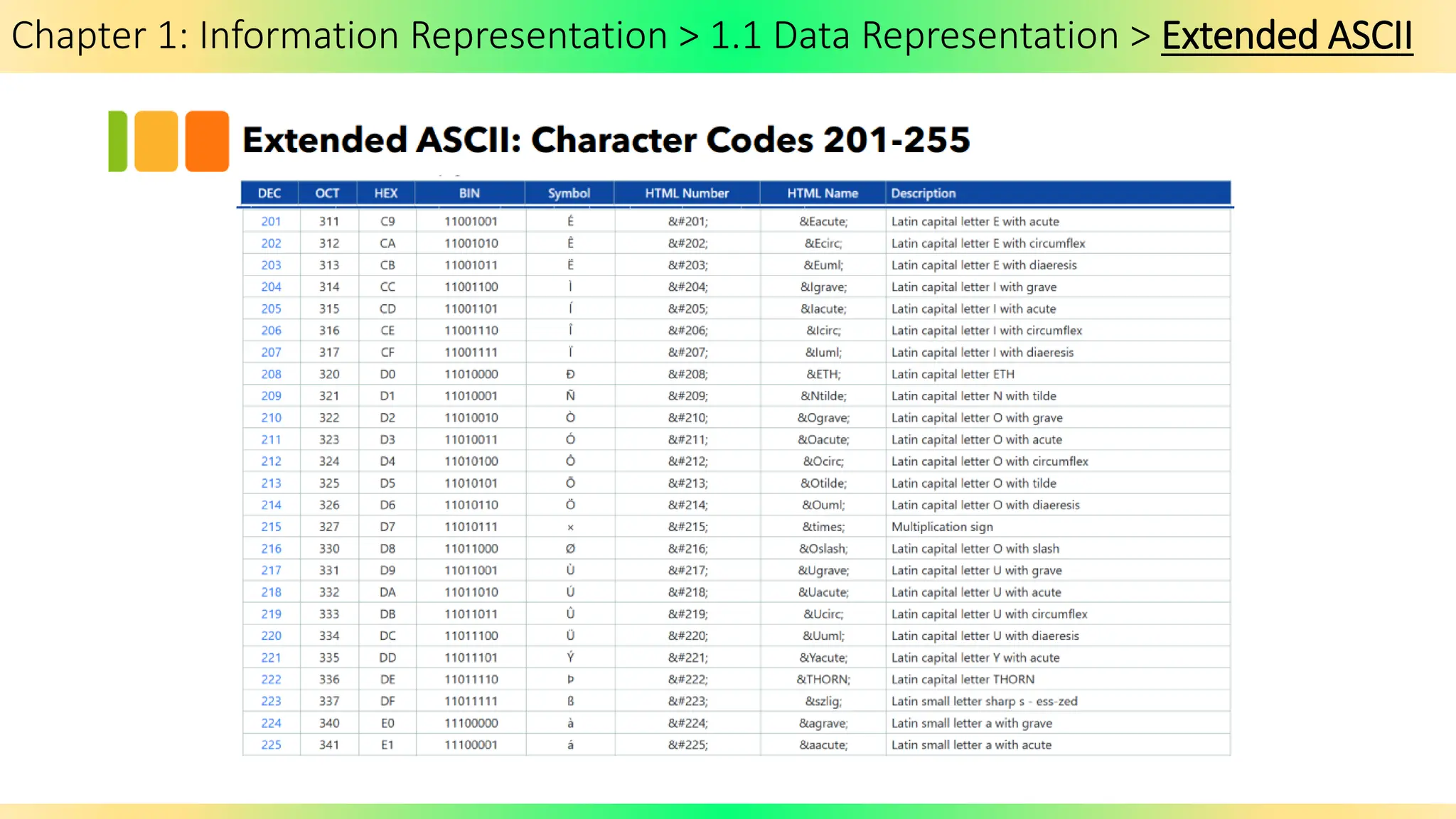
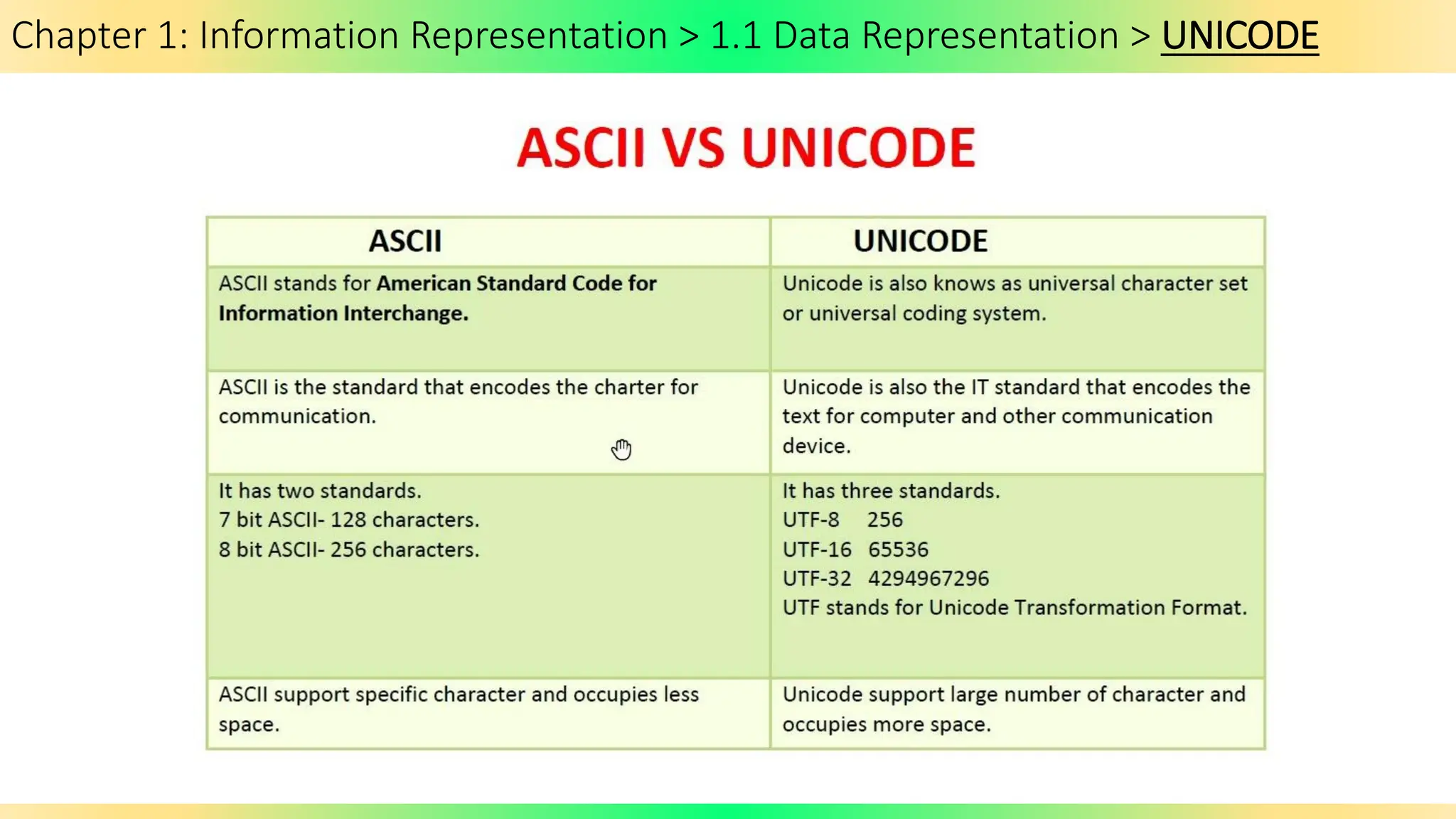
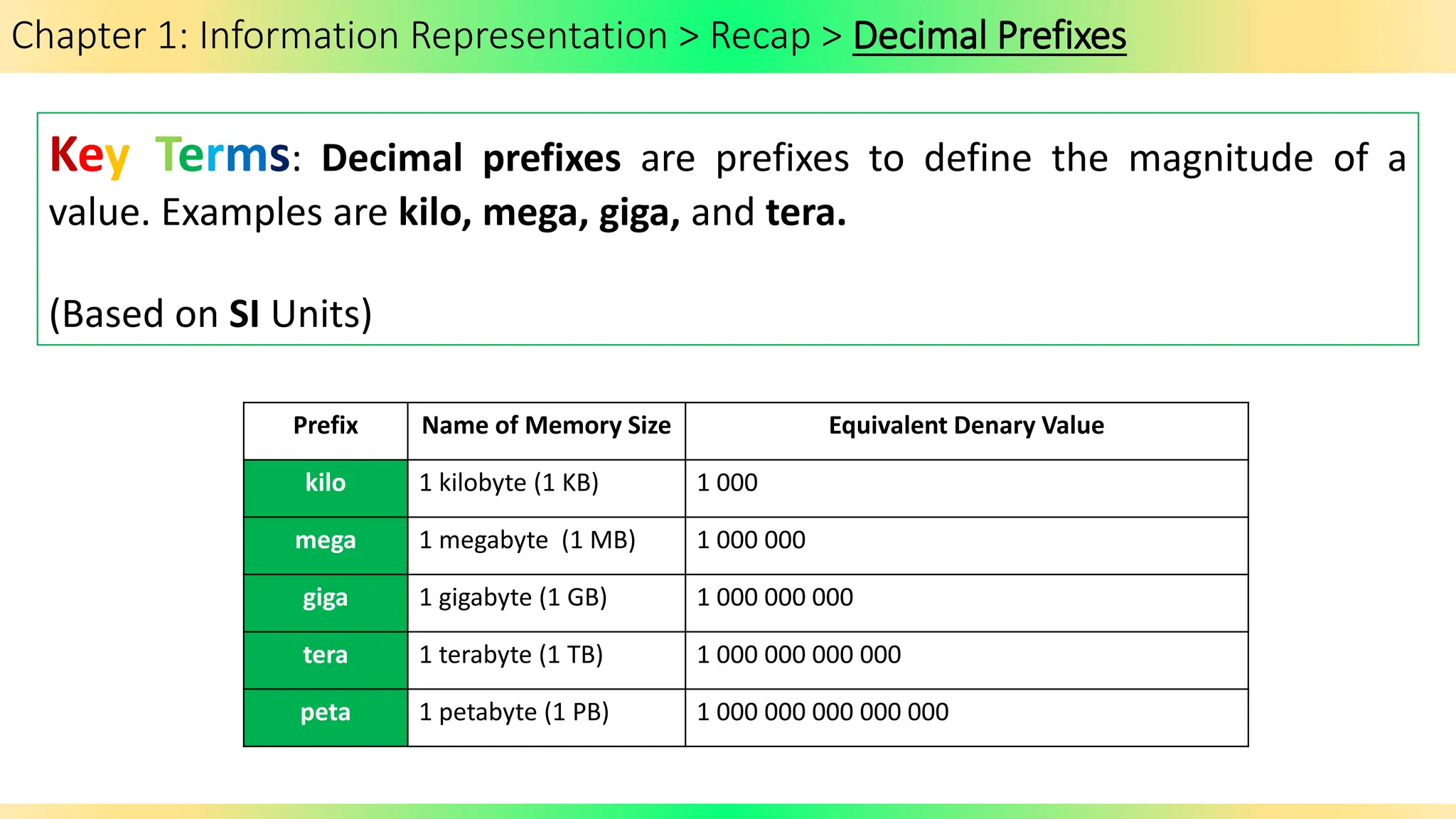
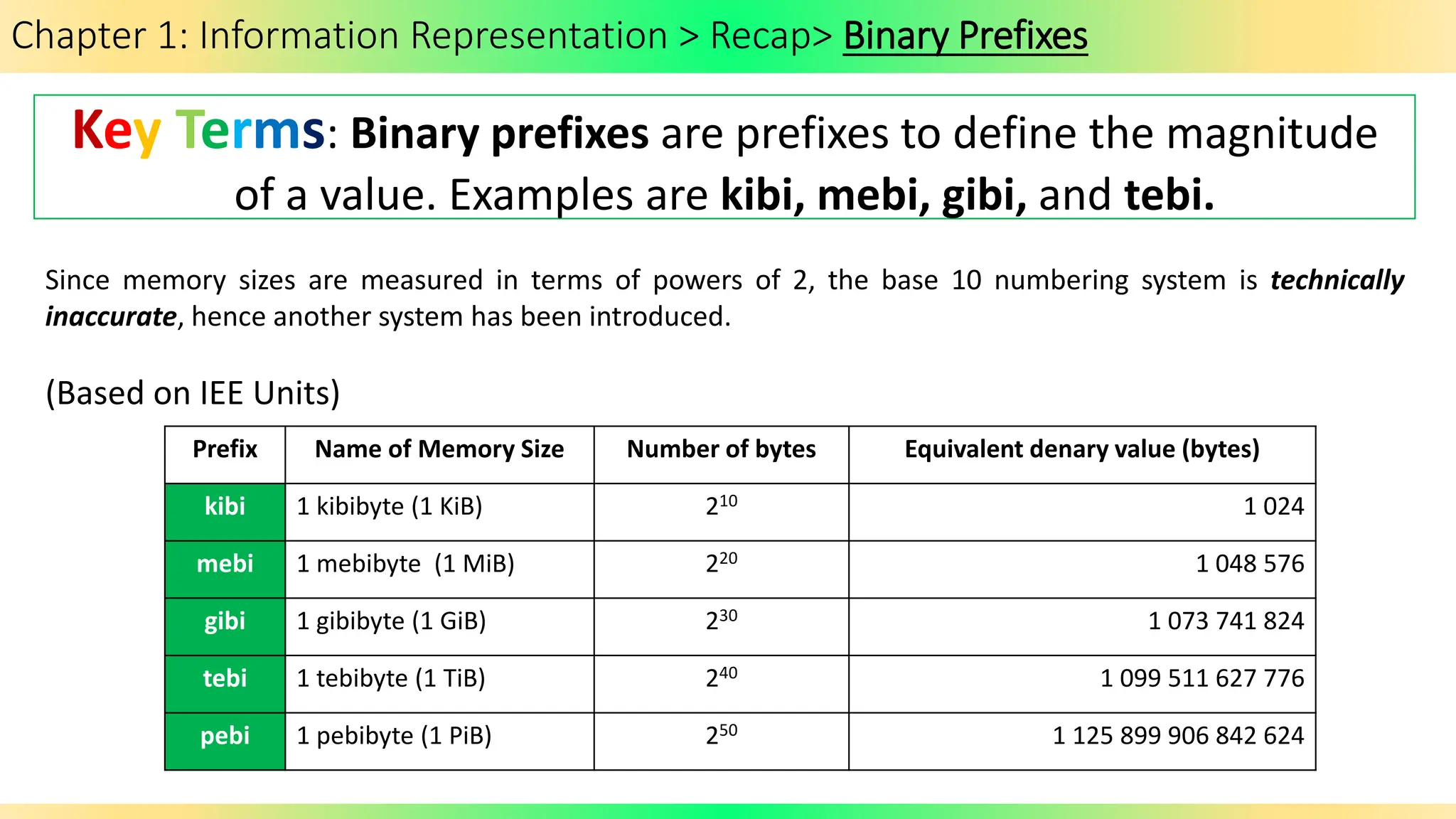
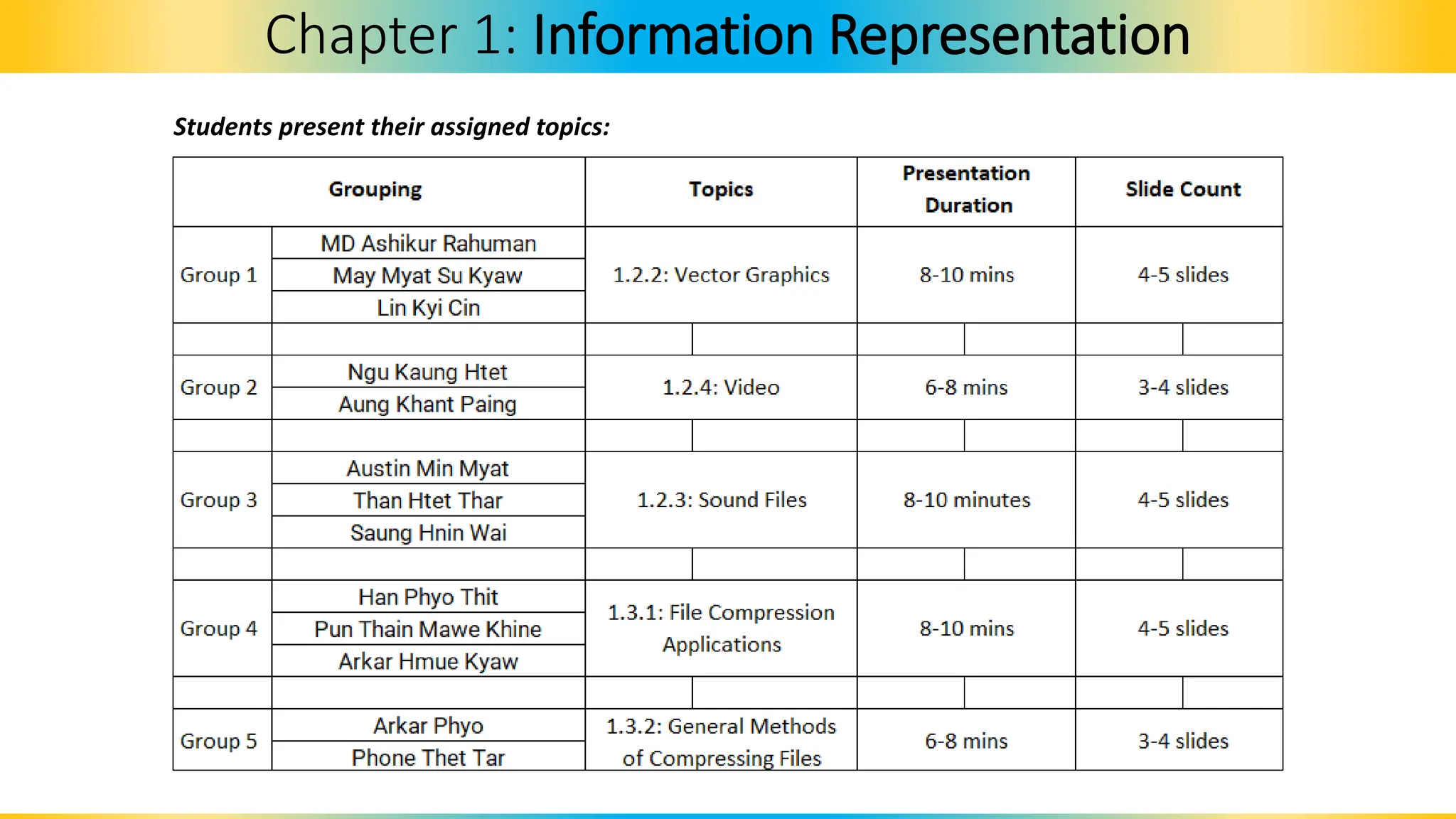
The document covers Chapter 1 of the AS/A Level Computer Science syllabus, focusing on information representation and data representation methods, including binary magnitude, BCD, and binary prefixes. It introduces key concepts such as signed binary numbers, image encoding in multimedia, and the advantages of BCD in digital displays. The chapter also touches on file compression methods and various multimedia types, guiding students through related exercises and applications.