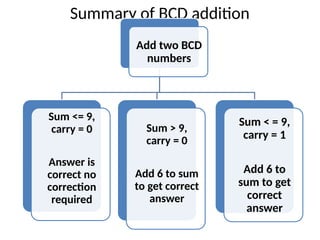
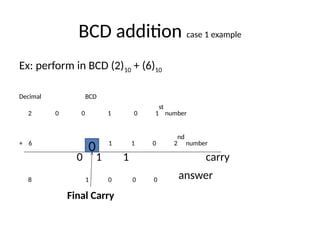
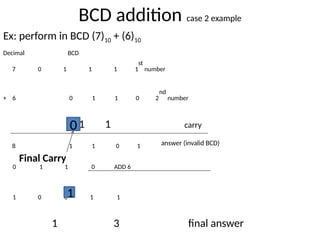
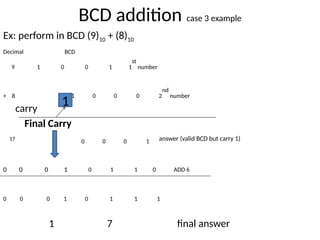
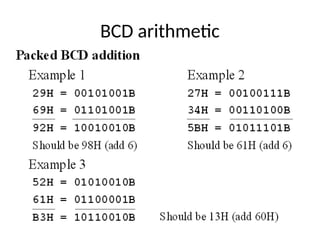
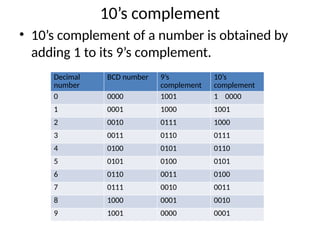
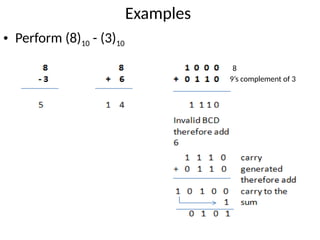
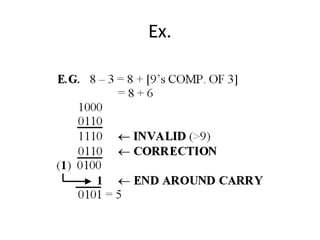
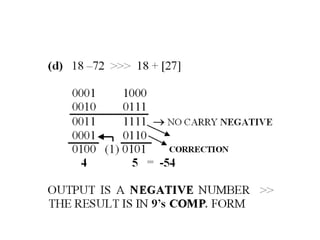
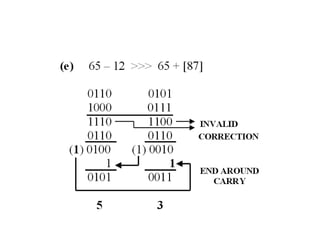
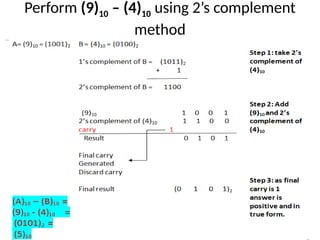
The document explains BCD (Binary-Coded Decimal) addition and subtraction techniques, detailing the handling of carries and corrections needed when results exceed valid BCD ranges. It includes examples for both addition and subtraction using 9's and 10's complement methods. Additionally, it provides steps and examples for performing BCD operations with decimal numbers.

1. BCD Addition and subtraction

2. BCD addition
Add two numbers as same as binary addition
Case 1: If the result is less than or equals to 9
and carry is zero then it is valid BCD.
Case 2: If result is greater than 9 and carry is
zero then add 6 in four bit combination.
Case 3: If result is less than or equals to 9 but
carry is 1 then add 6 in four bit combination.

3. Summary of BCD addition
Add two BCD
numbers
Sum <= 9,
carry = 0
Answer is
correct no
correction
required
Sum > 9,
carry = 0
Add 6 to sum
to get correct
answer
Sum < = 9,
carry = 1
Add 6 to
sum to get
correct
answer

4. BCD addition case 1 example
Ex: perform in BCD (2)10 + (6)10
Decimal BCD
2 0 0 1 0 1
st
number
+ 6 0 1 1 0 2
nd
number
0 1 1 carry
8 1 0 0 0 answer
0
Final Carry

5. BCD addition case 2 example
Ex: perform in BCD (7)10 + (6)10
Decimal BCD
7 0 1 1 1 1
st
number
+ 6 0 1 1 0 2
nd
number
1 1 carry
8 1 1 0 1 answer (invalid BCD)
0 1 1 0 ADD 6
1 0 0 1 1
1 3 final answer
0
Final Carry
1

6. BCD addition case 3 example
Ex: perform in BCD (9)10 + (8)10
Decimal BCD
9 1 0 0 1 1
st
number
+ 8 1 0 0 0 2
nd
number
carry
17 0 0 0 1 answer (valid BCD but carry 1)
0 0 0 1 0 1 1 0 ADD 6
0 0 0 1 0 1 1 1
1 7 final answer
1
Final Carry

7. BCD arithmetic

8. Solve?????
1. Perform in BCD (57)10 + (26)10
2. Perform in BCD (83)10 + (34)10
3. Perform in BCD (421)10 + (975)10

9. 9’s complement:
9’s complement of a BCD number can be
obtained by subtracting it from 9.
10’s compliment:
10’s compliment is obtained by adding 1 to 9’s
compliment

10. 9’s complement
• The 9’s complement of BCD number is
obtained by subtracting it from 9.
• Ex: 9’s complement of 1 = 9 – 1 = 8
Decimal number BCD number 9’s complement
0 0000 1001
1 0001 1000
2 0010 0111
3 0011 0110
4 0100 0101
5 0101 0100
6 0110 0011
7 0111 0010
8 1000 0001
9 1001 0000

11. Find the 9’s complement
• 9’s COMPLEMENT of 28 = 99 – 28 = 71
• 9’s COMPLEMENT of 562 = 999 – 562 = 437

12. 10’s complement
• 10’s complement of a number is obtained by
adding 1 to its 9’s complement.
Decimal
number
BCD number 9’s
complement
10’s
complement
0 0000 1001 1 0000
1 0001 1000 1001
2 0010 0111 1000
3 0011 0110 0111
4 0100 0101 0110
5 0101 0100 0101
6 0110 0011 0100
7 0111 0010 0011
8 1000 0001 0010
9 1001 0000 0001

13. BCD subtraction
• Two methods:
1. 9’s complement method
2. 10’s complement method

14. BCD subtraction using 9’s complement
• Perform BCD subtraction using 9’s
complement method (A)10 - (B)10
1. Obtain 9’s complement of no. B
2. Add no. A and 9’s complement of no. B
3. If carry is generated in step 2 then add it to sum to
obtain final result. The carry is called as end around
carry.
4. If carry is not produced then the result is negative
hence take 9’s complement of the result.

15. Examples
• Perform (8)10 - (3)10
9’s complement of 3
8

16. Ex.

17. Ex.

18. Ex.

21. Solve following subtraction of decimal
numbers using 9’s complement method.
1. Perform (7)10 - (3)10
2. Perform (4)10 - (7)10
3. Perform (83)10 - (21)10
4. Perform (52)10 – (89)10

22. BCD subtraction 10’s complement method
• Perform BCD subtraction using 10’s
complement method (A)10 - (B)10
1. Obtain 10’s complement of no. B
2. Add no. A and 10’s complement of no. B
3. If carry is generated in step 2 then discard it.
4. If carry is not produced then the result is negative hence take 10’s complement
of the result.

23. Example using 10’s complement

24. Solve following subtraction of decimal
numbers using 9’s complement method.
1. Perform (7)10 - (3)10
2. Perform (4)10 - (7)10
3. Perform (83)10 - (21)10
4. Perform (52)10 – (89)10

25. 9’s complement and 10’s complement

26. Perform (9)10 – (4)10 using 1’s complement method

27. Perform (4)10 – (9)10 using 1’s complement method

28. Solve
• Perform following subtraction using 1’s
complement method.
1. (-5)10 - (-7)10
2. (48)10 – (61)10
3. (33)10 – (54)10
4. (99)10 – (22)10

29. Perform (9)10 – (4)10 using 2’s complement
method

30. Perform (4)10 – (9)10 using 2’s complement
method

31. Solve
• Perform following subtraction using 2’s
complement method.
1. (-5)10 - (-7)10
2. (48)10 – (61)10
3. (33)10 – (54)10
4. (99)10 – (22)10
5. (1010)2 – (101)2