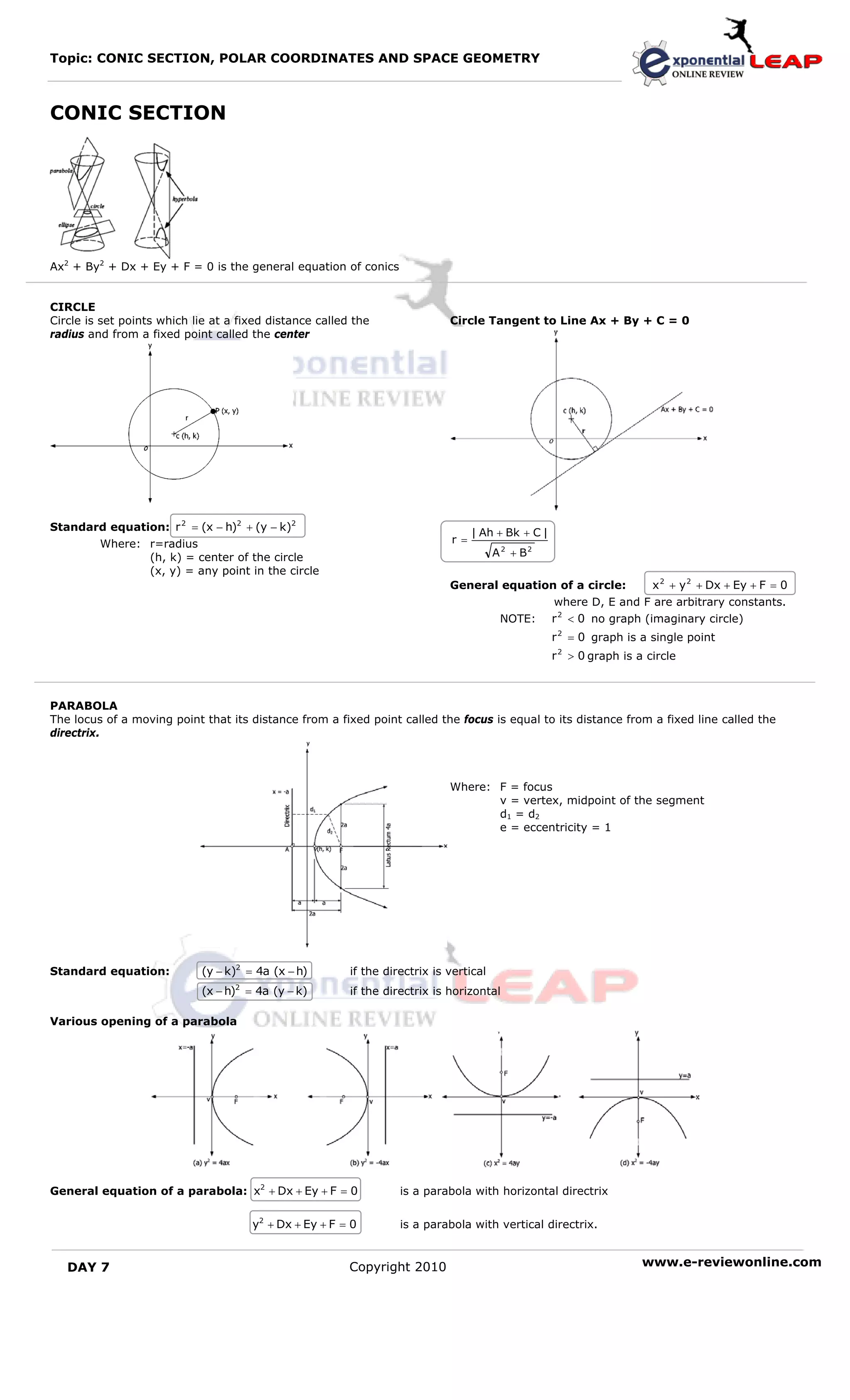
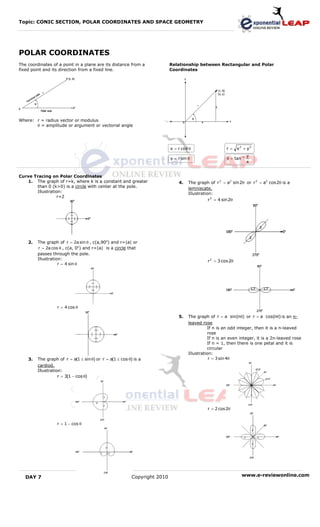
1. The document discusses conic sections such as circles, parabolas, ellipses, and hyperbolas defined by standard and general equations. 2. It also covers polar coordinates and how to trace curves using polar equations like r=k, r=a±b sinθ, and r=a(1±sinθ). 3. Additionally, the document introduces concepts of space geometry like the three dimensional coordinate system, planes, cylinders, spheres, and quadratic surfaces including ellipsoids, hyperboloids, paraboloids.

1. Topic: CONIC SECTION, POLAR COORDINATES AND SPACE GEOMETRY
CONIC SECTION
Ax2 + By2 + Dx + Ey + F = 0 is the general equation of conics
CIRCLE
Circle is set points which lie at a fixed distance called the Circle Tangent to Line Ax + By + C = 0
radius and from a fixed point called the center
Standard equation: r 2 = (x − h)2 + (y − k)2 | Ah + Bk + C |
Where: r=radius r =
(h, k) = center of the circle A 2 + B2
(x, y) = any point in the circle
General equation of a circle: x 2 + y 2 + Dx + Ey + F = 0
where D, E and F are arbitrary constants.
NOTE: r 2 < 0 no graph (imaginary circle)
r 2 = 0 graph is a single point
r 2 > 0 graph is a circle
PARABOLA
The locus of a moving point that its distance from a fixed point called the focus is equal to its distance from a fixed line called the
directrix.
Where: F = focus
v = vertex, midpoint of the segment
d1 = d2
e = eccentricity = 1
Standard equation: (y − k)2 = 4a (x − h) if the directrix is vertical
2
(x − h) = 4a (y − k) if the directrix is horizontal
Various opening of a parabola
General equation of a parabola: x2 + Dx + Ey + F = 0 is a parabola with horizontal directrix
y2 + Dx + Ey + F = 0 is a parabola with vertical directrix.
DAY 7 Copyright 2010 www.e-reviewonline.com

2. Topic: CONIC SECTION, POLAR COORDINATES AND SPACE GEOMETRY
ELLIPSE
An ellipse is a set of points in a plane, such that the sum of the distances of each from two fixed point is a constant. The fixed points
are called the foci and the line through them is the axis.
Where: F1, F2 = focus
v1, v2 = vertex, midpoint of the segment
d1 + d2 = 2a
d c
e = eccentricity = 3 = < 1
d4 a
a
d=
e
a2 = b 2 + c 2
2b 2
LR = Latus Rectum =
a
(x − h)2 (y − k)2
Standard equation: 2
+ =1 if the major axis, M.A. is parallel to the x-axis
a b2
(y − k)2 (x − h)2
2
+ =1 if the major axis, M.A. is parallel to the y-axis
a b2
General equation of an ellipse: Ax 2 + By 2 + Dx + Ey + F = 0 where A and B is greater than 0
NOTE: M < 0 no graph (imaginary ellipse)
M = 0 graph is a single point
M > 0 graph is an ellipse
D2 E2
M = −F + +
4A 4B
HYPERBOLA
A hyperbola is a set of points in a plane, such that the difference of the distances of each from two fixed point is a constant. The
fixed points are called the foci and the line through them is the axis.
Where: F1, F2 = focus
v1, v2 = vertex, midpoint of the segment
d1 + d2 = 2a
d c
e = eccentricity = 3 = >1
d4 a
a
d=
e
c 2 =a2 +b 2
2b 2
LR = Latus Rectum =
a
Equation of Asymptote
Asymptote of a curve is a line when the perpendicular distance from a line to a curve approaches zero as the curve extends
indefinitely far from the origin.
y − k = ±m(x − h)
Where (h, k) is the center of the hyperbola and m is the slope, m=b/a if the axis is horizontal and m=a/b if the axis is
vertical. Use (+) for upward asymptote and (-) for downward asymptote.
(x − h)2 (y − k)2
Standard equation: − =1 if the transverse axis is parallel to the x-axis (Opens left and right)
a2 b2
(y − k)2 (x − h)2
2
− =1 if the transverse axis is parallel to the y-axis (Opens up and down)
a b2
Length of transverse axis (TA) = 2a
Length of conjugate axis (CA) = 2b
Length of the focal axis (FA) = 2c
General equation of hyperbola: Ax 2 + By 2 + Dx + Ey + F = 0 where A or B is less than 0
DAY 7 Copyright 2010 www.e-reviewonline.com

3. Topic: CONIC SECTION, POLAR COORDINATES AND SPACE GEOMETRY
POLAR COORDINATES
The coordinates of a point in a plane are its distance from a Relationship between Rectangular and Polar
fixed point and its direction from a fixed line. Coordinates
Where: r = radius vector or modulus
θ = amplitude or argument or vectorial angle
x = r cos θ r = x2 + y2
y
y = r sin θ θ = tan −1
x
Curve Tracing on Polar Coordinates
1. The graph of r=k, where k is a constant and greater 4. The graph of r 2 = a2 sin 2θ or r 2 = a2 cos 2θ is a
than 0 (k>0) is a circle with center at the pole. lemniscate.
Illustration: Illustration:
r=2
r 2 = 4 sin 2θ
2. The graph of r = 2a sin θ , c(a,90o) and r=|a| or
r = 2a cos θ , c(a, 0o) and r=|a| is a circle that
passes through the pole.
Illustration:
r 2 = 3 cos 2θ
r = 4 sin θ
r = 4 cos θ
5. The graph of r = a sin(nθ) or r = a cos(nθ) is an n-
leaved rose
If n is an odd integer, then it is a n-leaved
rose
If n is an even integer, it is a 2n-leaved rose
If n = 1, then there is one petal and it is
circular
Illustration:
3. The graph of r = a(1 ± sin θ) or r = a(1 ± cos θ) is a r = 3 sin 4θ
cardiod.
Illustration:
r = 3(1 − cos θ)
r = 2 cos 2θ
r = 1 − cos θ
DAY 7 Copyright 2010 www.e-reviewonline.com

4. Topic: CONIC SECTION, POLAR COORDINATES AND SPACE GEOMETRY
6. The graph of r = a ± b sin θ or r = a ± b cos θ is a limacon.
If |a| < |b| the graph is a limacon with inner loop
If |a| = |b| the graph is a cardiod
If |a| > |b| the graph is a limacon without a loop
Illustration:
r = 1 − 2 cos θ r = 4 + sin θ
SPACE GEOMETRY
Three Dimensional Coordinate System
Distance formula in three space Distance between a point (x, y, z)
and a plane
Ax 1 + By 1 + Cz 1 + D
d=
A 2 + B2 + C2
Midpoint formula
x + x2
x = 1
2
y1 + y 2
y =
2
z1 + z 2
z=
2
Cartesian coordinates (x, y z) d = (x 2 − x 1 )2 + (y 2 − y 1 )2 + (z 2 − z1 )2
Plane
The graph of Ax + By + Cz = D is a plane
Illustration: Cylinders
Any equation in two variables, represents a
Graph: 2x + y + 3z = 6 cylindrical surface, that is perpendicular to the two
variables and whose generating curve is the plane
curve whose equation is given.
Illustration:
Graph: x2+z2=4
Sphere:
Standard equation: (x − h)2 + (y − k)2 + (z − l)2 = r 2
General equation: x 2 + y 2 + z 2 + Dx + Ey + Fz + G = 0
Illustration:
Graph: x 2 + y 2 + z 2 − 2x + 4y + 6z − 2 = 0 Graph: y2=4x
C(1,-2,3) and r = 4
DAY 7 Copyright 2010 www.e-reviewonline.com

5. Topic: CONIC SECTION, POLAR COORDINATES AND SPACE GEOMETRY
Quadratic Surfaces
1. Ellipsoid 3. Hyperboloid of Two Sheets
x2 y2 z2
2
+ 2
+ =1
a b c2
2. Hyperboloid of One Sheet x2 y2 z2
2
− 2
− =1
a b c2
4. Elliptic Paraboloid
x2 y2 z2
2
+ 2
− =1
a b c2
x2 y2
2
− =z
a b2
DAY 7 Copyright 2010 www.e-reviewonline.com